基于智能数据信息分析的就业评估方法研究

赵瑞丹

（西安航空职业技术学院，陕西西安 710089）

传统的就业数据来源于调查问卷（纸质或网络），以及高校的官方统计信息。但这两种方式均存在各自的问题，前者得到的数据较为有限，难以涵盖全部学生，后者保证了数量，但无法顾及每个学生的就业质量[1-3]。事实表明，即使在毕业时有确定的就业岗位，但仍有大批学生对职业有了充分了解后，在一年或更短时间内更换工作。因此，合理地评估就业质量也是需要关注的重要问题[4-5]。

在高速发展的信息化时代，新的行业不断产生，对人才的需求也迫切增加。学生就业质量的优劣，不仅能反映社会行业的发展趋势，且可以及时地反馈给高校，从而适当地调整专业分布，提高教育水平[6-7]。

面对大量的就业数据，不仅缺少从事质量评估的专业人员，且因评估人员的水平不足导致评价结果因人而异。近年来，兴起的人工智能与数据分析方法尤为适合应对此类问题。人工智能采用深度学习，可以模仿人脑对信息做出逻辑判断，评估隐藏在数据背后的就业质量[8-9]。文中采用智能信息分析，将采集到的就业数据通过层次分析方法和单层感知器，确定每种信息每次的相应权重，最终产生对就业信息的质量评估。

1 数据采集

1.1 第一阶段数据采集

数据采集包括两个阶段，第一阶段采集学生毕业前的就业信息，主要内容包括6 个大类：学生个人信息（编码A）、就业信息（编码B）、档案寄送地址（编码C）、就业单位性质（编码E）、工作性质（编码F）、个人满意度（编码G1）。每个大类均包含若干小类，除填写类信息外，选择类信息均对应着具体的数值。

第一阶段的个人满意度取值范围为0～100，表示学生对就业方向的满意程度，第一阶段的满意度占比为40%。

1.2 第二阶段数据采集

考虑到学生还未参与到实际工作中，对工作和前景的认知尚不充分。在就业12 个月后再采集一次就业数据，作为第一阶段数据的修正与补充。第二阶段的满意度由学生了解实际工作内容及行业知识后打分，具有更高的可信度，取值范围为0～100，占比为60%。从数据量化可以看出，第一阶段的数据主要用于建立就业信息资料库；第二阶段的数据用于输入信息分析网络训练集，估计出每一层数据的权重，从而实现就业质量的评估。

2 数据预处理

实际采样到的数据无法达到理想的采样状态，不能直接进入训练集中参与运算。首先对采样数据进行预处理，其过程包括：数据提取、相关性分析与离散化、数据清洗、数据集成4 个步骤[10-13]。

2.1 信息提取

考虑采集到的原始信息为3 种格式：文本格式、表格格式和图片格式。对于文本格式，使用Python自然语言处理，提取第一节中所述的类别信息。信息提取的基本过程，如图1 所示。

图1 文本类信息提取

表格类型的原始信息，多来源于院校发布，已极为接近理想的采样状态，直接进入下一步信息处理。

对于图片类型的采集信息，利用Python构造信息提取算法，先调用文字识别软件，提取图片中的文本和图形信息。再进一步提取和目标相关的数据，转换为表格类型的文件。信息提取过程如图2 所示。

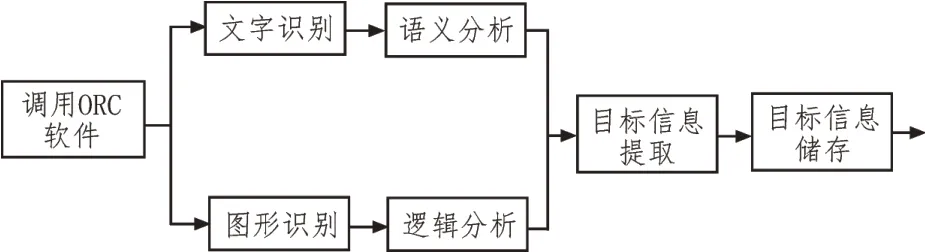
图2 图片类信息提取

2.2 相关性分析和离散化

对于采集所给类别之外的信息，按照相关性强弱的关系将其归纳到该系统的类别中，使用互信息来衡量这种相关性，互信息的计算公式如下：

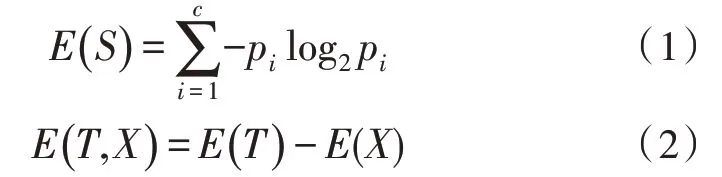
互信息可对文本特征值的相关性进行度量，将互信息值在（0.9，1）范围内的两种数据视为一类数据，进行合并。并将其具体值按类别的范围归纳到相关的子类[14]。

文本类信息仅保留A、B、C 类，其余数据均将舍弃文本，保留具体的数值。大多数类型要求采样到详细的数值，对于单个如“好”、“差”等语言描述类的采样数据，根据对应的取值范围，离散化为相应的数值。

2.3 数据清洗

按A～M 的顺序，检查数据集中的数据。删除重复项，计算数据集中的各个子类的均值和众数。当数据集的该项缺失在30%以下时，用众数补全缺失的数据；当缺失率达到50%～80%时，用均值补全缺失的数据；当缺失率达到80%以上时，从训练集中删除该子类[15]。数据的补全操作不包括A、B、C 项。

2.4 数据集成

每位学生的数据按照一个标准模板存放，称为标准数据包。以A 项数据为每个数据包的总类，存放下属的B～M 类样本数据及每个样本的值。对每个类别只保存一个子类的数值，例如H 项仅保存H1～H5 五项数据中的一项，及其对应的具体数值。

通过数据预处理可以计算出学校的就业率、升学率信息，计算公式如下：

3 质量评估模型的构建

3.1 层次分析法模型

层次分析算法包括3 个层次：最高层、最低层和中间层。最高层为要解决的问题，最低层为决策时的备选方案，中间层为决策要考虑的因素及决策的准则。基于这三层的质量评估模型如图3 所示。

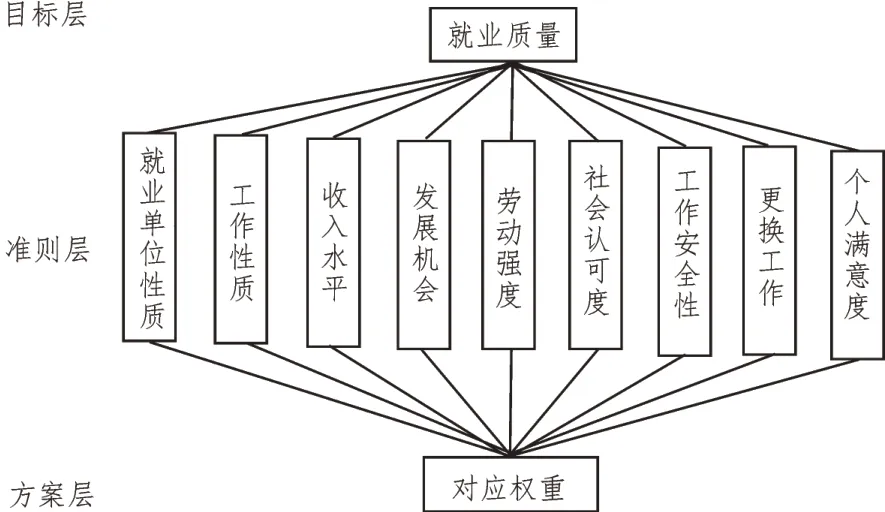
图3 层次分析法模型

3.2 构造判断矩阵

使用一致矩阵法构造各类对就业质量的判断矩阵。判断矩阵的元素由1～9 标度法给出，表示两个准则层的因素对于就业质量评判的重要性对比，如表1 所示。

表1 1～9标度含义

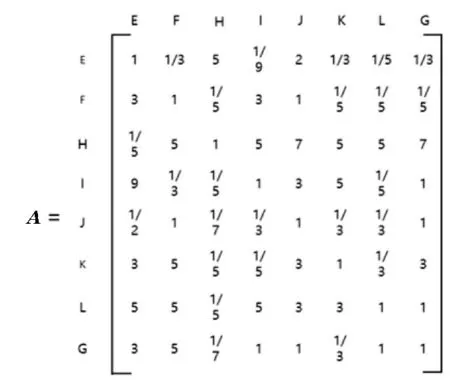
图4 依据重要性对比构造的判断矩阵

3.3 类别权重因子计算

为了使判断矩阵是成对比较阵，对判断矩阵的列求和，并将每个元素归一化，其公式如下：

计算所有元素的和，并对每行归一化。得到各指标对目标的权重，计算公式如下：

考虑到更换工作次数与就业质量成反向关系，且更换工作次数越多，说明就业的质量越低。因此对更换工作类单独建立二次项模型，参与后续计算。计算得到的各类别的权重因子，如表2 所示。

表2 各类别的初始权重

更换工作类参与质量评估的选定为：

3.4 使用BP算法降低误差

使用单隐藏层前馈网络模型来降低质量估计的误差，神经网络由两层神经元组成。输入层接收8 个类别的采样信息，隐藏层和输出层为M-P 神经元，模型如图5 所示[16]。

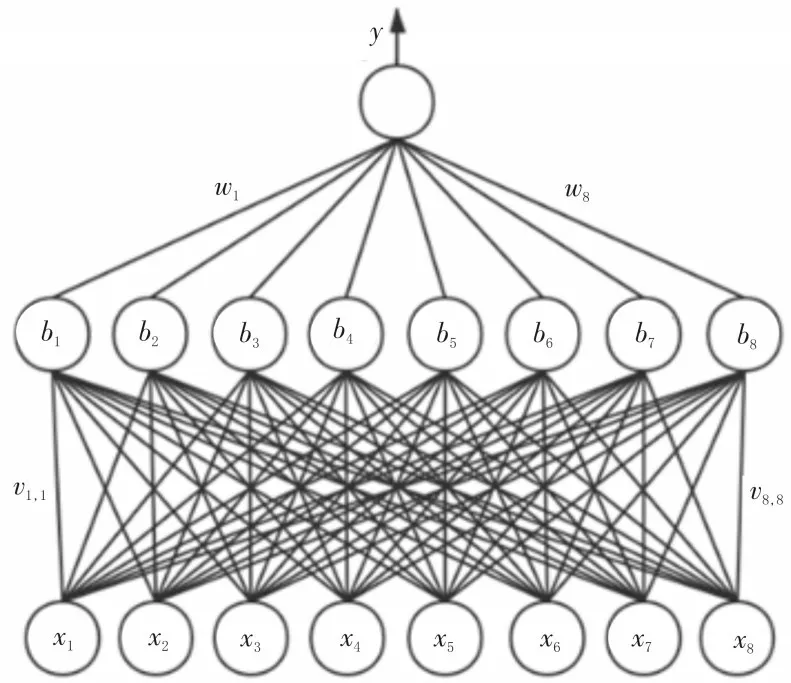
图5 单隐藏层神经网络模型

模型的隐藏层和输出层神经元的激活函数均采用Sigmoid 函数，公式如下：

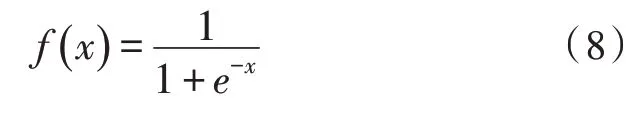
对于训练集(xk,y)，神经网络的输出为：

其中，β为输出层神经元的输入，θ为其阈值。隐藏层神经元的输入为wj，阈值为bj，而β可表示为：

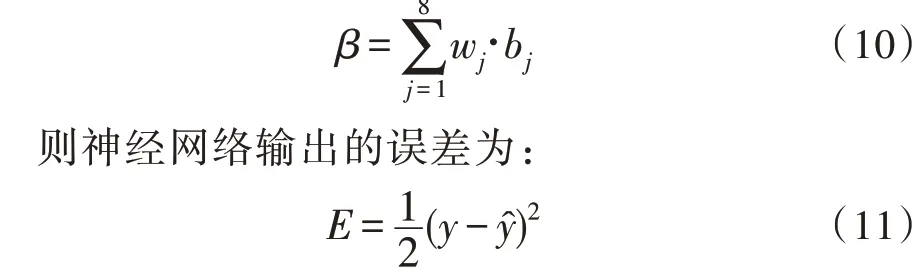
该网络共有8×2+8×8+1=81个参数待定，BP算法在每一轮迭代中对参数进行更新估计，更新公式为：

其中，η用于控制算法中每一次迭代的更新步长，η∈(0,1]。

BP 算法的流程总结如下：

1）输入训练集和学习率；

2）使用3.3 节得到的各类权值初始化w1,w2,…,w8。v1,1,v1,2,…,v8,8均初始化为0.5；

3）根据式（7）计算每个训练样本的神经网络输出；

6）根据式（13）～（16）更新神经元的连接权值及阈值；

7）重复步骤2）～6），以达到停止条件。

停止条件为使训练集上的累计误差最小，如式（19）所示。

4 模型仿真

文中使用Python 编写层次分析模型和单层感知器模型，仿真的训练集采用武汉大学发布的2019 届毕业生就业质量报告，并加以精简。学习率η设置为0.6，当神经网络输出达到稳定时，得到神经网络的各神经元连接权值和阈值。

使用构造的质量评估模型，评估2019 年某航空职业院校的3 492 名毕业生的就业质量。其中未就业137 人，就业率为96.08%，将已就业学生的数据分两次进行采集，经过量化和预处理以后输入到质量评估模型中，得到如图6 所示的专业评分数据结果。

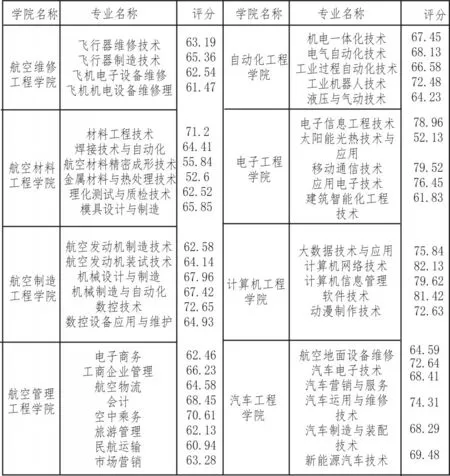
图6 基于该模型的某高校专业评分结果

5 结束语

文中结合机器学习和信息分析技术，为高校的就业质量评估提供一种新的方法。基于文中构建的质量评估模型得出的专业评分数据，与实际高校专业质量情况进行比较，结果基本一致，证明了该模型的可靠性。与传统一次性信息采集不同的是，文中选择时间间隔一年的两次就业数据采集，且就业质量的分析主要取决于第二次数据采集。实际操作过程中，遇到了样本较少的问题，但随着高校对毕业生的就业信息跟踪调查的力度加大，这一问题也将得到解决。

该系统的优点在于，采用人工神经网络可做出接近人类思维的决策，从而降低人力成本、时间成本。且随着样本数据的增多和训练集的扩展，会使评估结果更加可靠，系统的升级与误差修正也远比传统质量评估系统方便、简洁。