电路模型在光伏能量转换系统中的应用

胡珍妮，崔娟，卫军超

（西安交通工程学院，陕西西安 710300）

光伏领域（PV）在过去的二十年中经历了令人瞩目的发展，利用光伏阵列产生电能的最佳方法是将其直接输送到交流电源，而无需使用电池组。通过光伏系统进行的研究表明，在所产生的故障中，逆变器占比63%，模块占比15%，其他组件故障占比23%，平均每4.5年发生一次故障。为了降低光伏系统的故障率，有必要降低逆变器和组件（也称为系统的PV 平衡）的故障率[1-2]，这将导致其经济上的可行性。

目前，系统PV 平衡研究使用数学功能模型对新开发系统的性能进行分析，长期以来需要简化PV 模块的Simulink 建模。一些文献提出了通过人工智能技术间接调整I-V曲线的方法[3]，但这种方法较复杂而且需要很高的计算量。所以，建模仅限于对光伏组件特性的仿真。文中提出了采用简单电路模型的光伏系统设计，并详细介绍了光伏组件的电路模型，提出了控制PV 模块方程的Simulink 模型，并给出了不同辐照度和温度值的数值结果。由数值结果可以得出模块参数与PV 模块的特性曲线关系，其是电路性能的指标。经过适当的实验验证，得出了完整的电路模型，使用Simulink 对使用扰动和观察（P＆O）算法的MPPT 进行建模[4-5]，通过仿真验证了用于闭环MPPT 控制的DC-DC 升压转换器开发的电路模型的实用性。

1 光伏组件建模

1.1 等效电路

PV 模块由多个串联和并联的太阳能电池组成，以获得所需的电压和电流输出水平。每个太阳能电池基本上都是一个PN 二极管，当阳光照射到太阳能电池上时，入射能量无需任何机械作用即可直接转换为电能[6-7]。通过使用这种光能将自由电子从低能级激发到高能级，透射光被吸收到半导体内。当太阳能电池被照亮时，在整个材料中都会产生多余的电子-空穴对，因此PN 结短路，电流流动。为简单起见，文中使用图1 所示的单二极管电路模型。该模型通过电流源和并联二极管组成的基本结构在简单性和准确性之间取得了很好的折衷。在图1 中，Iph为电池光电流，Rp和Rs分别为电池的固有并联电阻和串联电阻。

图1 单二极管电路模型

1.2 光伏组件方程

光伏电池被分组在更大的单元中，称为光伏模块，它们在串联-并行配置中进一步相互连接，形成光伏阵列。

图1 中，光伏模块的光电流Iph线性依赖于太阳辐射，同时也受温度的影响，其公式如下：

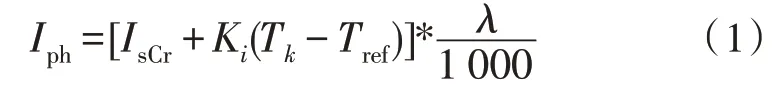
其中,Ki为短路电流温度系数，其值为0.001 7 A/K，Tk和Tref分别是实际温度和参考温度，单位为K，λ为器件表面的辐照度，单位为W/m2，标称辐照度为1 000 W/m2。

图2显示了式（1）中光电流的详细Simulink模型。

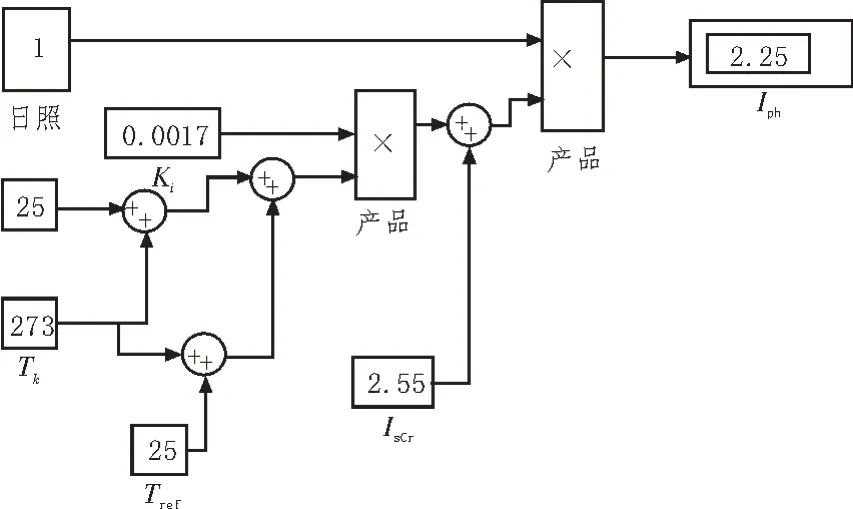
图2 光电流的Simulink模型

1.3 模块反向饱和电流

模块反向饱和电流Irs由式（2）给出。

式中，q为电子电荷(1.6×10−19C)，VOC为Solkar 模块开路电压(21.24 V),Ns为串联单元数，值为36)，k为玻尔兹曼常数(1.380 5×10−23J/k)，A为理想系数，值为1.6。式（2）的详细Simulink 模型如图3 所示。

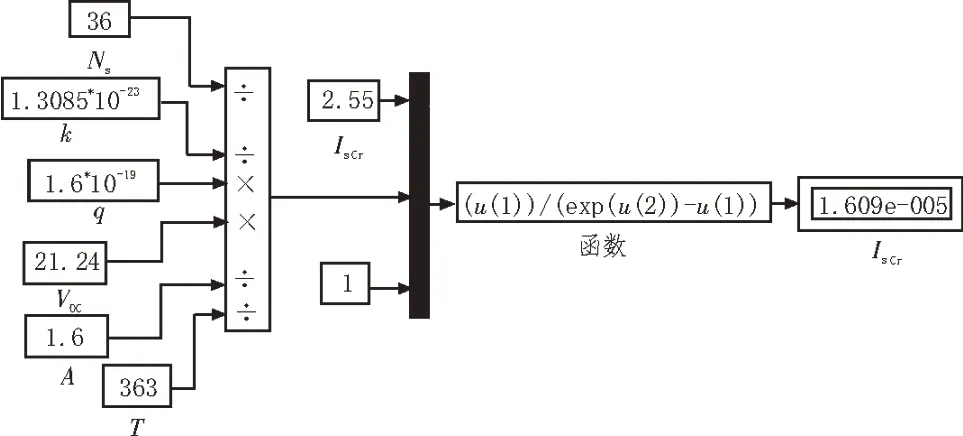
图3 模块反向饱和电流Simulink模型

模块反向饱和电流随温度变化的关系如表1所示。

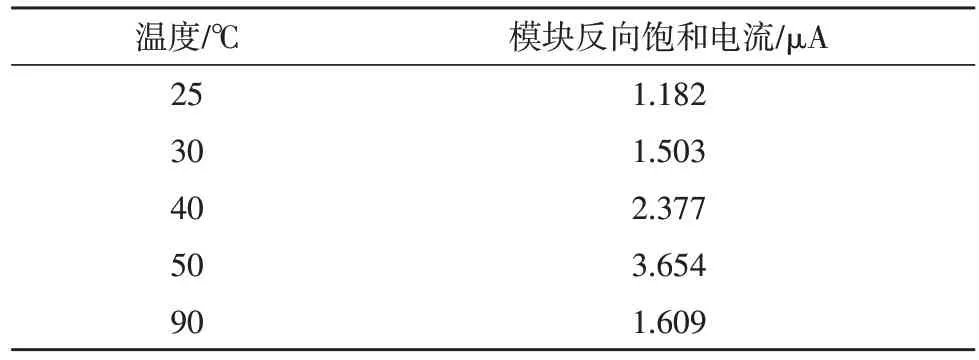
表1 不同温度下的Irs

1.4 模块饱和电流

模块饱和电流I0随电池温度变化，公式如下：

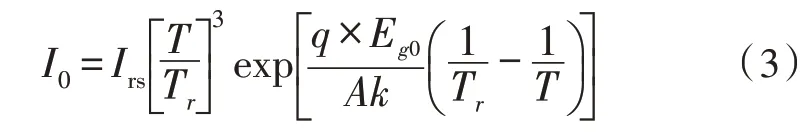
其中，Eg0是半导体的带隙能,即指价带与导带之间的能量(对于多晶硅，在25 ℃下Eg0≈1.1 eV)。对该方程进行仿真，以模块工作温度、参考温度和模块反向饱和电流作为输入，计算了不同温度下的模块饱和电流I0。

1.5 模块输出电流

单二极管PV 模块的输出电流IPV由式（4）给出:

式中，Np、Ns分别为给定光伏模块中电池并联和串联的次数(Np=1,Ns=36)，VPV=VO=21.24 V，Rs为模块的等效串联电阻，Rsh为等效并联电阻。

电流泄漏、隧道效应、微等离子体击穿、沿表面通道泄漏等被建模为一个平行电阻。当电压最低时，通过等效电路二极管的电流很小时，并联电阻的影响最大。当并联电阻足够小时，并联电阻的作用是降低开路电压和填充系数[8-9]，短路电流不受影响。不同Rsh值下PV 模块的相对辐照效率如图4 所示。从图4 中可以看出，Rsh值较大时，组件效率下降了3%～5%。当Rsh很小时，组件效率可以忽略。在这种情况下，仅在较低的隔离值下，模拟值将比实际值高出3%～5%。然而，在正常/较高的隔离值下，不会有任何明显的变化。文中采用简化的电路模型，通过该模型可以使电力电子设计人员找到一种简单有效的模型来模拟具有电力转换器的光伏器件。并联电阻Rsh的值一般较高，因此忽略了简化模型，如式（5）所示。串联电阻Rs（0.1 Ω）是PV 组件几个结构电阻的总和，尤其在最大功率点区域附近，其影响更大。

图4 相对辐照效率

式（5）的求解需要迭代，需要在Simulink 中求解代数循环。为避免这一问题，在PV 研究中采用功能模型对PV 模块进行建模。

1.6 IPV的Simulink模型

将以上模块进行互连，得到光伏模块的IPV的Simulink 模型。该模型以日照、温度和PV 为输入。实验电路描述如下：

1）运放、MOSFET 和电阻连接，使太阳能电池板的电流与运放非逆变端口的电压成正比[10-11]；

2）采用线性MOSFET。闸源极端口的MOSFET是由一个低频三角波信号驱动的；

3）使用了DSO，因此不需要重复触发信号，只需要一个缓慢变化的斜坡信号将电流从零改变为短路值即可；

4）曲线拟合平滑后的仿真和实验V-I特性如图5 所示。

图5 仿真和实验V-I特性

从图5 可以看出，模拟的电流在仿真时的数值为2.55 A。在较高的日照值下，该模型的模拟电流值比实验电流值高出约2%，因此该电路模型具有合理的精度。

2 面向电路的光伏组件模型

在光伏电池的等效电路中，整个光伏电池的可用电压为PN 结正向偏置电压，光伏组件开路电压为21.24 V/36≈0.6 V，IPV的Simulink 模型给出了模块当前的IPV。这个PV 电流由辐照度和温度计算出来，作为输入直接用于电路模型中。模型输出端的电压作为IPVSimulink 模型的电压输入Vin反馈。

光伏组件的详细电路模型如图6 所示，其中，二极管的正偏置电压取19 V(表示36 个光伏电池的串联)，这是有用电压电平的较高值。这里，首先选择一个电压值，由于涉及到代数环问题，因此按照正泛函PV 模型的方法对功率方程进行迭代。

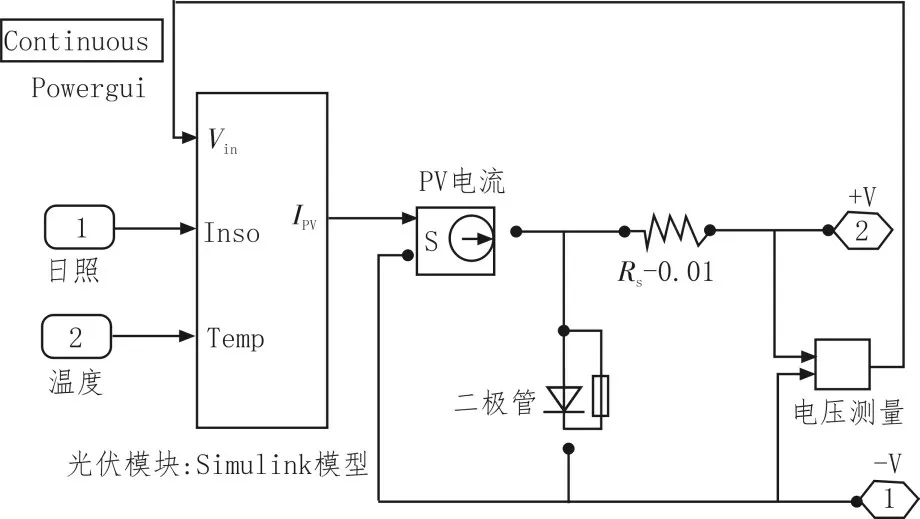
图6 PV模块电路模型

3 PV最大功率提取系统设计

随着辐照度和温度的变化，光伏组件的功率输出是连续变化的。文中采用最大功率点跟踪(Maximum Power Point Tracking,MPPT)算法提取太阳能光伏组件的最大功率[12-14]，并将其传输到负载。DC-DC 变换器的作用是将PV 模块的最大功率传输到负载，并作为负载和模块之间的接口。通过改变PWM 控制信号的占空比，源负载阻抗发生变化并与源的峰值功率点匹配，从而传输最大功率。

3.1 电力电子电路

PV 模块通常与DC-DC 转换器一起使用，以获得最大的功率点。使用的转换器类型有buck、boost和buck-boost。对于电池充电应用程序，buck-boost配置是首选的，DC-DC boost 转换器通常用于光伏系统，以将低模块电压提高到高负载电压。因此，文中采用DC-DC boost 变换器设计MPPT 控制器。

3.2 DC-DC boost变换器的设计

boost 变换器配置由直流输入电压源Vs、升压电感L、控制开关S、二极管、滤波电容C、负载电阻R组成。当开关工作的占空比为D时，boost 变换器的直流电压增益为：

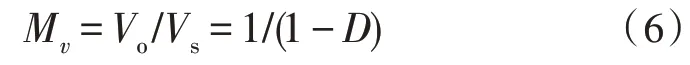
其中，Vs为输入电压，Vo为输出电压，D为控制MOSFET 开、关状态的脉宽调制信号的占空比。boost 转换器在连续导通模式下工作，电感值L>Lb，其中：

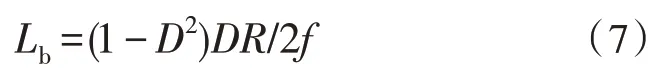
式中，Lb为连续导电时电感的最小值。输出RC电路的电流是不连续的，因此，需要一个较大的滤波电容器来限制输出电压纹波。当二极管断开时，为负载提供输出直流电流的滤波电容器的最小值为Cmin，计算公式如下:

3.3 MPPT设计

采用带直流电源的boost 转换器电路的电池供电方式对DC-DC 变换器进行仿真。在直流电源下[15-16]，变换器的升压比与占空比成正比。将boost转换器电路的电池电源替换为第2 节中开发的电路模型，并进行仿真。在MPPT 的设计中，利用所建立的电路模型进行仿真数据收集。在较低的辐照值和恒载情况下，辐照度1 000 W/m2时占空比为0.41，辐照度500 W/m2时占空比为0.2，如图7 所示。

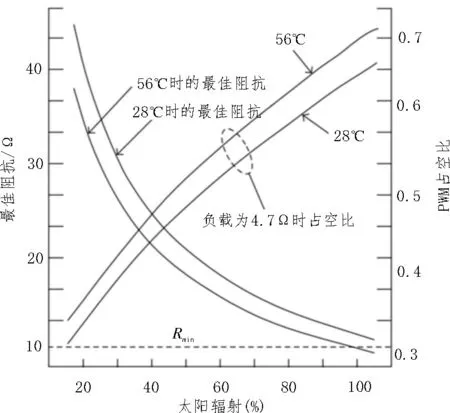
图7 占空比随太阳辐射的变化

3.4 MPPT控制算法

已有文献中提出了许多MPPT 技术,例如扰动和观察(P&O)、电导增量(IC)、模糊逻辑等。P&O 算法是非常流行和简单的,所以文中使用P&O 算法。在P&O 算法中，系统引入了轻微的扰动(ΔD=0.01)，这种扰动导致太阳能组件的功率发生变化。如果功率由于扰动而增加，则扰动在该方向上继续（D+ΔD）。达到峰值功率后，下一个瞬间功率降低，之后扰动反转（D-ΔD）。将Vin和Iin作为MPPT 单元的输入，得到占空比作为输出，将上述MPPT 单元作为闭环控制置于仿真电路中[17]。

4 讨论

DC-DC 升压变换器作为PV 模块与负载的接口，软件会感测电压和电流输出，并生成数字误差信号，将数字误差信号交给DAC(0808)，DAC 将其转换为相应的模拟信号。将该信号与20 kHz 的高频三角波进行比较，产生的脉冲被给定到功率半导体器件(MOSFET)的门，从而改变变换器的占空比。所产生的脉冲必须能够触发MOSFET 的电源电路，从而使源阻抗与负载阻抗匹配，传输最大功率。

微控制器编程应该按照占空比范围来进行，以获得更快的响应，实验是在25 ℃下进行的。与仿真值相比，PV 模块功率和电流的实验值降低了约2%～5%。因此，在闭环控制中，所建立的电路模型的性能符合仿真值，且具有合理的精度。

5 结论

文中提出了光伏（PV）模块的电路模型。光伏电流Iph是太阳辐照的函数，是光能转化为电能的唯一能量转换参数。光伏电压是半导体材料特性二极管结电压的函数，在较高温度下容易失效。文中用各种温度下模块饱和电流的数值详细介绍了控制光伏模块（也适用于光伏电池）的物理方程式，该电路模型给出了模块参数与电路性能之间的关系。利用最大功率点跟踪算法的闭环控制转换器对设计电路进行了仿真，且结果通过了验证，即在闭环控制中，所建立的电路模型的性能符合仿真值，且具有合理的精度。