基于小波变换的图像信号分解与重构

冯晶晶，陈文利，董丹凤

（1.西安培华学院智能科学与信息工程学院，陕西西安 710125；2.西安交通大学第一附属医院，陕西西安 710061）

信号处理是现代科学技术发展的重要部分，它已被广泛使用于科学、工程、技术等方面。对于平稳信号的处理，传统的方法是利用Fourier 变换，而对于非平稳信号的有效研究技术则是小波分析。小波变换是研究图像信号处理领域的一个有力工具，小波理论已被广泛应用到图像压缩、特征提取、信号滤波、数据融合、故障诊断、神经网络等方面[1-5]。

从数学角度来看，图像可看作是二维信号，所以信号与图像的处理都可看作是信号处理。小波分析的许多应用[6-10]都可归结为信号处理问题。将小波理论应用于图像处理，就是利用多分辨分解，将图像分解为不同空间和不同频率的子图像，再对子图像进行系数编码。同时，小波变换较好地解决了时间和频率分辨率的矛盾，因此小波变换非常有利于图像信号的分解与重构。该文通过研究由尺度函数生成的多分辨分析、两尺度关系，得到小波对信号的分解算法和重构算法，这种算法用于信号与图像压缩和传递，压缩比高，压缩速度快，压缩后能保持信号与图像的特征不变，而且在传递过程中可以抗干扰[11-14]。

1 信号的分解与重构

1.1 多分辨分析的性质

首先介绍由尺度函数φ(x)生成L2(R)的多分辨分析问题[15-17]。

1.2 小波对信号的分解算法和重构算法

在L2(R) 中，{ }Vk是其中一个多分辨分析，Vk+1关于Vk的补空间为Wk，设fN(x)为f(x)在VN中的投影，则对f(x)∈L2(R)，有

用数据传递示意图表示信号分解，如图1 所示，其中↓2 表示只剩下样数的一半。

图1 小波分解示意图

又有两尺度序列{pn}、{qn}，则信号重构算法为：

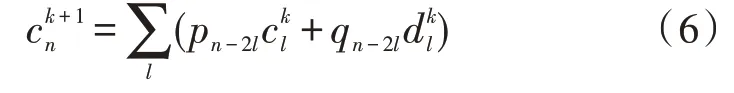
用数据传递示意图表示信号重构，如图2 所示，其中↑2 表示得到的样数为原来的2 倍。

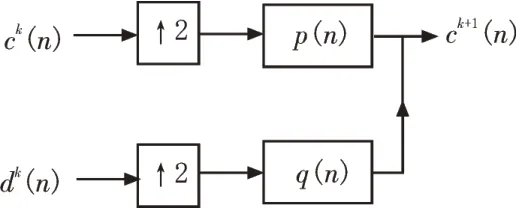
图2 小波重构示意图

2 图像的分解与重构

2.1 二元张量积多分辨分析

2.2 小波对图像的分解算法和重构算法

图像分解示意图如图3 所示，其中L表示低频，H表示高频，下标1、2 表示一级或二级分解。用数据传递示意图表示小波分解数据流，如图4 所示。

图3 图像小波分解示意图

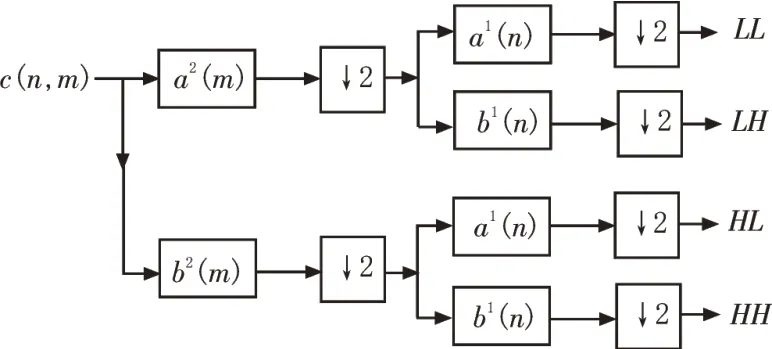
图4 小波分解数据流示意图

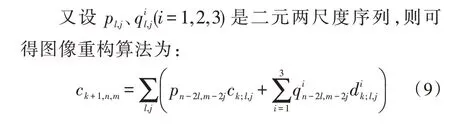
重构的数据传递示意图如图5 所示。

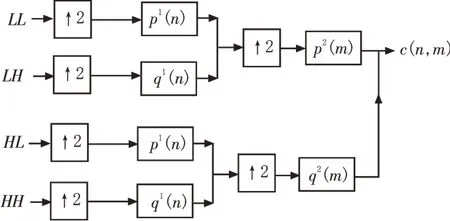
图5 重构的数据传递示意图

使用sym5 对图像进行分解，可以看出低频部分包含了图像的主要信息，如图6 所示，反映图像的基本原貌，高频反映了图像的细节信息，如图7所示。

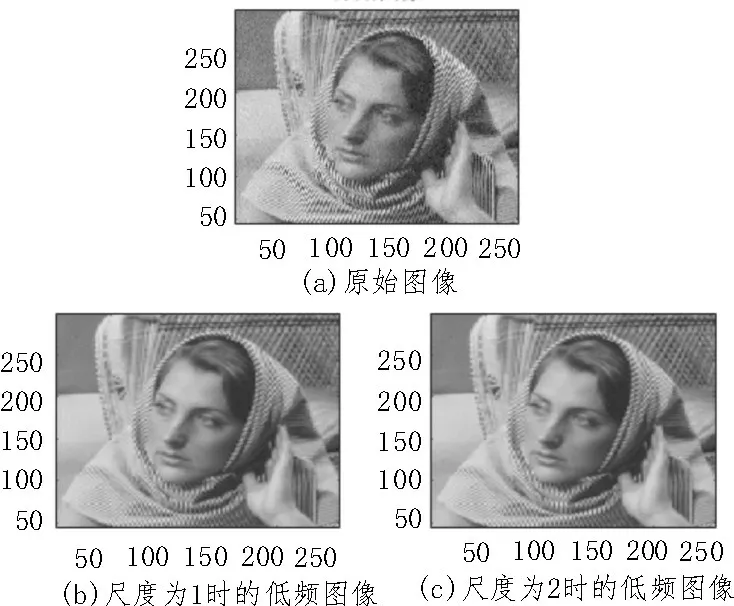
图6 sym5对图像的低频分解

图7 sym5对图像的高频分解

3 结论

采用小波变换对图像信号进行分解和重构，通过尺度变换、多分辨分析，能有效地从图像中提取信息。采用Matlab 小波工具箱，使用sym5 对图像进行低频和高频分解，可以看出，分解的尺度数、选取的小波基函数都会对图像产生影响，运用小波变换对信号与图像进行压缩，压缩比高，压缩速度快，压缩后能保持信号与图像的特征不变，而且在传递过程中抗干扰。