研究生光学仿真实践教学与科学探索能力培养
江 萍,杨华军,蔡杨伟男,秦 琰,邬劭轶
(电子科技大学 物理学院,四川 成都 611731)
2016年,在贵州落成并启用500米口径的球面射电望远镜“中国天眼”,为目前世界最大望远镜,开创了建造巨型射电望远镜的新模式. 同年8月,“墨子号”量子科学实验卫星在酒泉通过“长征二号”运载火箭成功发射升空,标志着我国空间科学研究迈出重要一步. 中国“嫦娥四号”探测器实现人类首次月背软着陆,是2019年国际十大科技新闻之一. 2020年,新冠肺炎疫情暴发后,我国科学家率先查明病源并分享基因序列,赢得世界赞誉. 党的十八大以来,以习近平同志为核心的中共中央把科技创新放在国家发展全局的重要位置,科技领域取得了一大批重大成果. 事实表明,理论和实践相结合,科学研究与工程应用相结合,才能绽放绚丽的花火.
当前我国正在大力弘扬新时代科学家精神,为建设科技强国汇聚磅礴力量. 科研人员是科技强国的中坚力量,研究生是不可或缺的生力军.目前研究生教学中主要存在自主创新能力培养不足,理论、仿真与实践脱节等问题. 作为高校教育工作者,培养研究生敢为人先的创新精神、严谨治学的求实精神、集智攻关的协同精神,为国家战略需求领域之科学与工程技术研究培养复合型人才任重道远.
本团队将光学系统设计、光通信前沿技术、高等光学等研究生课程建设与空间光通信领域的研究热点和前沿相结合,针对光电技术、微纳光学、量子通信技术领域发展需求,开展重理论基础、强创新实践、突科教融合的创新实践教学改革[1,2].
1 主要建设内容与特色
结合国外先进教材,将前沿技术领域(光通信、微纳光学等)科研项目纳入课堂教学中,开设学科前沿讲座和小班研讨课,完善课程内容,充实课程体系,强化科研促教理念,为我校物理学、光学、光学工程专业研究生编程实践能力、科学探索能力和科技论文撰写能力培养提供软硬件实践环境.
2 编程实践与挑战性案例解析
设置了基础光学、现代光学、综合应用三个层次的实践案例,题目均来源于科研项目及光通信最新研究进展,难度由低到高,设计思路如图1所示.

图1 案例设计思路
2.1 基础光学案例解析
运用Matlab编程对基础光学中非球面和非序列光学系统进行仿真,为研究生进入科研论文撰写阶段提供专业理论知识储备和编程实践能力训练.
2.1.1 案例1:非球面透镜设计与像差分析
题目:非球面在矫正高级球差、提高成像质量等方面有较高优势.设计旋转对称非球面透镜,实现平行光束完善成像.
教师指导过程如下:玻璃和空气折射率分别为n和n′,平行光聚焦到平凸透镜后f处.根据等光程原理,后表面为旋转双曲面,子午截线方程为
(1)
图2中下半平面光线(h<0)为双曲面平凸透镜光线追迹仿真结果,对于平行于光轴入射的光束,该透镜可以消除轴上球差.

图2 透镜光线追迹仿真结果与球面耦合透镜球差曲线
构建球面平凸透镜,像方光线(图2中上半平面h>0光线)不能聚焦到一点从而产生球差δL.
2.1.2 案例2:非序列光学系统仿真——直角棱镜
题目:非序列光线追迹是指任何光线没有预定路径,投射到任意物体上可能被反射、折射、衍射、分裂,棱镜、LED扩展光源等设计均属于非序列类型,编程仿真实现对直角棱镜的非序列光线追迹.
该案例旨在使学生掌握非序列光线追迹方法,培养自主编程实践能力.直角棱镜由3个相互垂直的等腰直角反射面构成,从底面入射的光线经过多次反射,由于光线经反射面的顺序不同,利用矢量反射定理更直观、易于编程.矢量反射定理为
A2=A1-2(A1·N1)N1
(2)
A1为入射光线单位矢量,N1为反射面的法线矢量,A2为反射光线矢量.空心直角棱镜(角反射器)和实心直角棱镜(角锥棱镜)的非序列光线追迹结果如图3所示,出射光束与入射光束相互平行.

图3 直角棱镜非序列光线追迹仿真结果
进一步对大口径直角棱镜阵列进行优化设计,研究阵列排布、入射光方向、有效反射面积等,该模型对激光雷达系统研究具有重要意义.
2.2 现代光学案例解析
为充分反映光学学科及相关领域的交叉融合,将现代光学与工程应用相融合,对大口径拼接天线、变折射率介质和光子晶体光纤进行建模与仿真.
2.2.1 案例3:大口径拼接光学天线理论建模与仿真实验
题目:大口径望远镜如天眼(FAST)、哈勃望远镜等均采用拼接结构,拼接结构广泛应用于大口径光学天线、太阳能聚光器中.基于矢量旋转和矢量反射定理,对大口径拼接光学天线进行建模与仿真.
图4为拼接主镜中六边形子镜向量示意图.
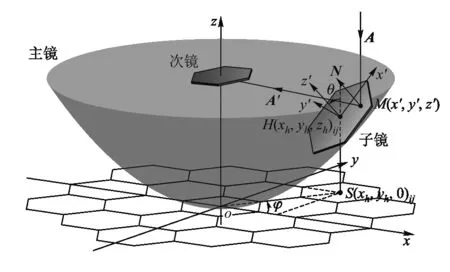
图4 拼接主镜中六边形子镜的位置和方向向量图
平面xoy上坐标(x,y,z)与子镜上点坐标(x′,y′,z′)关系为[x′,y′,z′,1]=[x,y,z,1]T,旋转矩阵[3]为
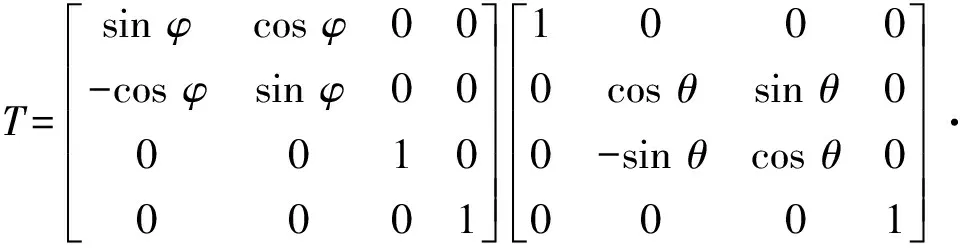
(3)


图5 拼接主镜三维光线追迹仿真结果
基于该模型对不同子镜结构进行优化设计,研究次镜离轴、偏焦对光传输性能的影响.本案例将仿真实践与工程应用相结合,加强创新思维的启发.
2.2.2 案例4:变折射率自聚焦光纤和准直透镜仿真
题目:径向变折射率透镜具有数值孔径大、直径小、自聚焦、成像分辨率高等特点,采用离子交换工艺,开拓了光学研究新领域,在光纤通信、国防军事等领域有广泛应用.分析径向变折射率介质的成像特性,设计自聚焦光纤和准直透镜.
教师指导过程如下:在傍轴近似下,径向变折射率介质中光线轨迹方程的矩阵形式为

(4)
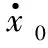

(a)自聚焦光纤仿真结果 (b)径向变折射率准直透镜仿真结果图6 案例4仿真结果
2.2.3 案例5:光子晶体光纤仿真实验
题目:布拉格光纤是一种一维光子晶体光纤,包层为径向折射率呈周期分布的多层介质,因此具有与普通光纤不同的色散特性.设计针对光通信传输波长1.55 μm的布拉格光纤,纤芯为空气,优化设计包层结构,对纤芯磁场分布进行仿真.
教师指导过程如下:布拉格光纤横截面和介质包层折射率分布分别如图7(a)、7(b)所示.

(a)布拉格光纤横 (b)布拉格光纤包层折射率分布 截面结构示意图图7 布拉格光纤结构及折射率分布
Λ为包层周期,纤芯半径为ρ1,z轴为光传播方向,在圆柱坐标系中,根据电磁场理论,布拉格光纤中磁场分量Hz表示为
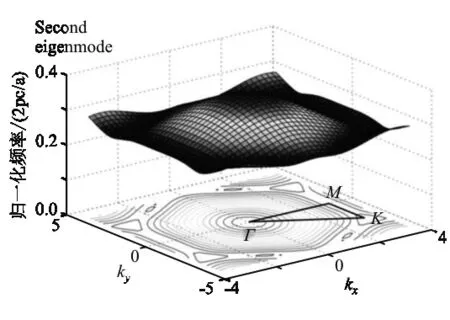
Hz=ccJl(kcr),(0 (5) 其中Jl(kr)为第一类贝塞尔函数,包层厚度为λ/4,纤芯折射率nc=1,ρ1=1 μm,包层折射率分别为n1=3和n2=1.5,厚度为l1=0.130 μm和l2=0.265 μm,二维和三维磁场分布仿真结果如图8.在此基础上对布拉格光纤的电场分布进行仿真,研究色散特性,加强编程实践能力综合训练. (a)布拉格光纤磁场分布曲线 (b)磁场三维分布仿真结果图8 案列5仿真结果 为充分反映光学学科领域内最新学术研究成果,将科研项目课题内容纳入课堂教学与仿真实践中实施科研促教,开展学科前沿和研究生小班研讨课程,通过光通信综合应用挑战性实践案例,进一步加强研究生创新实践与科学探索能力训练. 教师指导过程如下:正折射率介质中波矢k为正数,代表前向波,坡印廷矢量S与k平行,E、H和k满足右手正交系(图9(a)),正折射率介质也称为右手介质.负折射率介质中k为负数,代表后向波,S与k反向平行,E、H和k满足左手正交系(图9(b)),负折射率介质也称为左手介质.当电磁波从空气(n=1)入射到均匀左手介质(ε=-1、μ=-1、n=-1)中,发生负折射,折射光线和入射光线位于法线同侧,仿真结果如图9(c)所示. (a)右手介质 (b)左手介质 (c)电磁波负折射归一化电 场分布仿真结果图9 左手与右手介质中E、H、k和S之间的 关系以及电场仿真 右手介质中相位速度Vp与k方向相同,左手介质中Vp与k方向相反.一束水平传输的单色脉冲平面波入射到45°界面,均匀左手介质(n=-1)中Vp指向界面,发生负折射,仿真结果如图10所示. 图10 一束脉冲平面波从空气入射到均匀左手介质(n=-1)的归一化电场分布仿真结果,(a)、(b)为两个不同时间节点 当脉冲波第一个平坦波前到达界面后,脉冲波前速度Vs沿正折射方向,与能量传播速度相关的群速度Vg发生负折射.由于左手介质中S与k反平行,因此Vg与Vp反向平行.无论是左手介质还是右手介质中,Vg>0,这是因为传输波的能量始终沿远离界面的方向向前传播. 题目:光子晶体是一种介电常数成周期分布的非均匀介质,布拉格散射产生能带结构.基于负折射理论,研究光子晶体中的正向波和后向波传输特性. 教师指导过程如下:光子晶体因各向异性不属于左手材料.通过对光子晶体的结构及光子能带进行合理设计,也可以实现所需频段的负折射.在低频段(kx,ky)空间中等频线(EFCS)与各向同性介质中的EFCS相似,为以倒格对称点为中心的同心圆,相应频率范围内的光子晶体可视为有效折射率介质.在硅(εr=12)背景材料中制作空气孔形成六角晶格光子晶体,空气孔半径为0.4a(a为晶格常数).TE偏振态本征模的能带面与EFCS如图11[4]. (a)第一本征模能带面及EFCS (b)第二本征模能带面及EFCS图11 六角晶格光子晶体TE偏振态 对于归一化频率在ω=0.001(2πc/a)和ω=0.210(2πc/a)间的第一本征模(图11(a)),EFCS是以第一布理渊区内Γ点为圆心的同心圆.对于ω=0.300(2πc/a)和ω=0.360(2πc/a)间的第二本征模(图11(b)),EFCS也接近圆形.计算这两个频段内有效折射率neff曲线如图12(a),沿Γ-M和Γ-K方向的有效折射率曲线重合,表明该光子晶体在两个频段内均可视为有效折射率介质. (a)有效折射率neff曲线 (b)ω1=0.315(2πc/a)负折射和ω2=0.170(2πc/a)负折射仿真结果图12 案列7仿真结果 如图12(b)所示,两束不同频率的光束沿Γ-M方向以30°入射到光子晶体界面,负折射发生在ω1=0.315(2πc/a),对应于neff=-1,光子晶体中Vg与Vp反向平行,为后向波传输.正折射发生在ω2=0.170(2πc/a),对应于neff=2.5,光子晶体中Vg与Vp平行,方向相同,为前向波传输.该案例将微纳光学中的负折射与光子晶体理论相融合,对研究生创新能力和科学探索能力进行拓展训练. 题目:涡旋光(vortex beam)由于横截面光强呈环形分布且具有螺旋波前,在光通信、光操纵、成像等领域具有重要的应用,是光学学科研究热点.将空间光调制器(SLM)加载螺旋相位板、透镜和光阑相叠加的灰度图构建等效螺旋透镜,对平行光场进行调制,产生拓扑荷数和焦距可控的涡旋光场. 平面光场经等效螺旋透镜后的光场函数为[5] (x1+imy1)lPe(x1,y1) (6) 其中E0(x1,y1)为入射光场,Pe(x1,y1)为光阑函数,l为拓扑荷数,fy=m2fx,m为椭圆系数,fx和fy分别为椭圆螺旋透镜的横轴焦距和纵轴焦距.傍轴和远场近似下等效螺旋透镜后z处的截面光场为 (7) λ为入射光波长. (a)l=4,f=20 cm的等效螺旋透镜产生的衍射光场 (b)焦平面上的光强分布 (c)焦平面上的相位分布仿真结果图13 案例8仿真结果 实验装置如图14(a)所示,加载在SLM上的等效螺旋透镜产生拓扑荷数和焦距可调控的涡旋光束,有效地减小实验系统的复杂度,提高了可控性. 图14 案例8 实验装置图及结果. (a) 实验原理图,(b) SLM上的圆对称等效螺旋透镜灰度图像和焦平面光强分布实验结果,(c) SLM上的椭圆等效螺旋透镜灰度图像和焦平面光强分布实验结果 图14(b)为圆对称等效螺旋透镜(l=4,m=1)的实验结果,焦平面光强分布与仿真结果(图13(b))相同,验证了该方法的正确性.由于圆对称等效螺旋透镜产生的空心光斑无法识别拓扑荷数,将椭圆等效螺旋透镜灰度图像(l=4,m=1.06,焦距为30 cm)加载在SLM上,衍射光斑的暗条纹数等于拓扑荷数(如图14(c)),本案例将前沿科研成果[5-7]融入研究生小班研讨课程,探索SLM在光通信中的应用,为后续研究提供设计思路和数据支撑. 将光通信、微纳光学、光量子通信等交叉学科前沿与研究生光学系统设计课程相结合,结合研究生小班研讨课程,通过基础理论和仿真实践相融合,科学研究与工程应用相融合,对培养研究生编程实践能力和自主创新能力取得显著教学效果.近年来指导研究生发表高水平SCI论文十余篇[3,5-14],连续三次获得电子科技大学教学成果奖一等奖,该实践教学方法在光通信前沿技术、高等光学等研究生课程中得到应用和推广. 本团队将光学系统设计、光通信前沿技术、高等光学等研究生课程建设与空间光通信领域的研究热点和前沿相结合,实施了重光学设计理论、强编程实践训练、突前沿科教深度融合的教学改革,培养研究生严谨的科学素养和缜密的科学思维,为国家战略需求领域之科学与工程技术研究提供人才储备.
2.3 综合应用案例解析
2.3.1 案例6:负折射率介质仿真实验
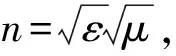


2.3.2 案例7:光子晶体中光传输特性仿真实验


2.3.3 案例8:涡旋光仿真实验
图13(a)为圆对称等效螺旋透镜(l=4,m=1)纵向光场仿真结果,图13(b)为z=20 cm处焦平面上光强分布,图13(c)为光斑相位分布.


3 课程建设与改革成效
4 结论

