三维声发射源定位实验简易实现方法

崔志文，尹莘新

(1. 吉林大学 物理学院，吉林 长春 130012；2. 重庆大学 航空航天学院，重庆 400044)

通过记录各种传感器接收的声波信号并对其进行适当分析，从而定位声源的过程通常被称为声源定位技术[1].声源定位实验是一个既有明确应用背景又有前沿技术特点的基础教学综合性实验[2].利用波的传播特性确定未知对象的空间位置，这种思想在无损检测(NDT)、全球定位系统(GPS)和地震研究等方面都有重要应用[1-3].

目前大学物理中的声源定位教学实验局限于二维板类结构[4，5]，三维结构的声发射源定位问题由于参数更多，往往需要借助大量的超声波传感器，配合多通道信号采集系统[6]，定位方法上需要求解复杂的非线性方程组，定位效果受速度测量和材料各向异性影响较大[7]，很难在教学上实现普及.对此本文基于时差法[3，8]提出一种可以快速实现三维声发射源定位实验的简易方法.本方法在减少硬件成本的同时简化定位过程，无需求解复杂非线性方程组，且不受材料的各向异性限制，达到快速定位三维结构中的声发射源的目的.通过本实验方案可以直观地向学生展现三维声源定位过程，加深学生对声发射技术及声源定位技术中物理问题的深入理解，提高学生对基于物理学声学原理的无损检测技术的兴趣，达到良好的实验教学目的.

1 实验原理

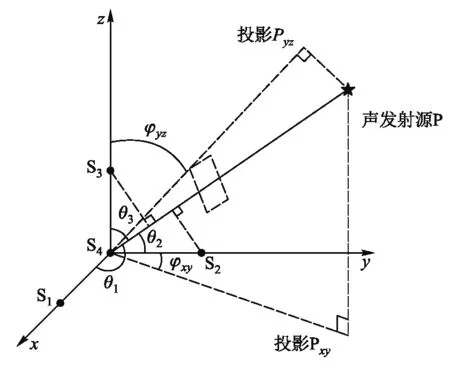
图1 声源与4个传感器位置示意图

在三维笛卡尔坐标系中，如图1放置4个超声波传感器，以传感器S4为原点，其他3个传感器S1、S2和S3分别位于x、y和z轴上与S4的距离为d处，形成一组直角四面体型传感器簇.声发射源P的坐标为(xp，yp，zp).传感器S1、S2、S3和S4的坐标分别为(x1，y1，z1)、(x2，y2，z2)、(x3，y3，z3)和(x4，y4，z4).可以看出x1=x4+d，y2=y4+d，z3=z4+d.通常传感器间距d应该比声发射源到任何一个传感器的距离小得多，意味着传感器簇到声发射源的距离足够远，此时声发射源的首个球形波阵面在到达一组传感器簇时可以近似看作平面波前[1].

由于声学事件生成声波的准确时间(T0)是未知的，因此很难从声波到达传感器Sm和Sn的时刻Tm和Tn获得精准的传播时间tm和tn.但是，声波的到达时差是很容易获得，从声源P到传感器Sm和Sn的传播时间差(Δtmn)就等于声波到这两个传感器的时刻差(ΔTmn)，

Δtmn=tm-tn=(Tm-T0)-(Tn-T0)=ΔTmn

(1)

如图1所示，当d<

(2)

其中c是声源到该传感器簇方向的声波速度.由于声发射源到同一组传感器簇中任一传感器的距离远远大于传感器之间的间距，所以同一传感器簇中的传感器接收到的声波信息除了有时间延迟以外，可以近似看作相同，声发射源到同一传感器簇的传感器S1、S2、S3和S4方向上的波速可认为是相同的，对各向异性材料这一假定也适用.

Pxy是声发射源P在xy平面上的投影，线PPxy垂直于xy平面，由立体几何中的“三余弦定理”可以得到

(3)

由此可以将S4Pxy和y轴之间的夹角φxy定义为

(4)

同样的，声发射源P在yz平面上的投影Pyz和z轴之间的夹角φyz可以表示为

(5)

声发射源P(xp，yp，zp)和原点传感器(0，0，0)确定的直线可以表示为

(6)

通过一组直角四面体型传感器簇的声波到达时差可以确定一条声发射源所在的直线，在三维结构的另一角落增加一组对称(或相同)直角四面体型传感器簇时，可以从第二组传感器簇获得声发射源的第二个方向，如图2所示，由此声发射源定位的过程就简化为求两条直线的交点.

图2 两组直角四面体型传感器簇定位声发射源示意图

传感器S5、S6、S7和S8的坐标分别为(x5，y5，z5)、(x6，y6，z6)、(x7，y7，z7)和(x8，y8，z8).如图2所示，容易看出x5=x8+d，y6=y8-d，z7=z8+d.通过第二组直角四面体型传感器簇的声波到达时差确定声发射源所在直线的投影与夹角为

(7)

声发射源所在的第二条直线可以表示为

(8)

根据两个直角四面体型传感器簇获得的两条声发射源所在直线，其交点就是预测的声发射源位置，整理为

(9)

因此，理论上均匀三维结构中的声发射源可以通过仅具有8个传感器的两个直角四面体型传感器簇定位，不需要提前测知材料特性，适用于各向同性及各向异性材料，无需解非线性方程组从而能够实现快速定位.

同时根据公式(2)和(3)，通过一组传感器簇的到达时差，不仅可以求出一条声源所在的直线，还可以求出该直线方向上的速度：

(10)

本文所用的时差皆为首波到达时差，三维结构中速度最快的波是纵波.声波在异质界面处会发生折射、反射、模式转换等现象，因此后到达的波成分复杂.本文提出的声发射源定位方法仅需专注于第一个到达的声波，对于所有传感器而言，最先接收到的波都是速度最快的纵波.

2 实验搭建

声发射实验通常使用多通道声发射信号采集系统，在声学事件发生时进行同时采集.由于多通道设备费用较高，本文的实验方案采用更为普遍的简单设备进行：示波器、单通道超声脉冲发射接收仪和两个150 kHz超声波传感器.实验样品为边长10 cm的铝制立方体和规格12 cm×14 cm×10 cm铁制长方体，以验证三维声发射源定位技术.

如图3所示，一个超声波传感器用于声发射源发射，另一个超声波传感器用作接收声波信号.由于超声波传感器的接触面是平面，故将立方体的一角切掉一个小直角四面体，以形成平坦的表面.将一个超声波传感器放置在此平面上，发射脉冲信号作为声发射源，在立方体的对角上标记出一组直角四面体型传感器簇的坐标，使用另外一个传感器依次在标记位置接收声波信号.假设铝制立方体沿一个方向延伸出一个对称的铝制立方体，那么整体三维结构的尺寸是其原始尺寸的两倍.第二个传感器簇相对于先前传感器簇对称(或相同)放置在该虚拟延伸的铝制立方体上，这组传感器簇的实验数据通过前一组实验的结果虚拟生成，即图3所示虚线部分.由此形成一个整体为10 cm×20 cm×10 cm的半虚拟三维结构作为实验样品.

图3 三维声发射源定位实验的示意图

同一传感器簇中位于正交方向的3个传感器距离位于原点传感器的间距d为2 cm.一个充当发射器的超声波传感器放置在声发射源位置，声发射源位置保持不变，另一个充当接收器的超声波传感器放置在S1、S2、S3和S4的标记位置，依次记录四个标记位置的声波信息，获得一组实际的传感器簇接收波形图.根据对称性，第二组传感器簇的接收波形图可以根据前一组对称得出.由于接收器不是点接收器，因此将接收器放置在接收点的侧面，它们需要平面接触表面，如图4所示.当接收传感器放置在与同一接收点相邻的垂直平面上时，第一波到达时间没有变化，这意味着只要接收传感器位于S1的接收传感器位置附近，放置在xy、yz和zx任意表面的效果都是一样的.

图4 三维声发射源定位实验系统的照片

3 实验结果

接收传感器接收到的声波图像如图5所示，通过获取首波到达的时刻差来获得不同传感器对(i和j)的到达时间差(Δtij).多次重复相同实验后的平均到达时间差用于预测声发射源的位置.图5所示的Δt是声波到达传感器S1和S4之间的时差.

将读取的时差带入理论部分，铝立方体的声发射源定位实验结果如图6所示，改变传感器簇位置，重复声发射源定位实验，结果如图7所示，实线是真实的铝立方体部分，而虚线是对称形成的虚拟铝立方体部分，来自两个传感器簇的两条线的交点是声发射源位置.从图6和图7的结果可以看出声发射源定位的结果并非是声源与传感器簇越近越准，这是因为声源与传感器簇距离太近时，首波的球形波阵面将不能被看作平面波.传感器在多个方向上多次测量了铝立方体中的P波速度，结果在6295 m/s左右，根据式(11)获得的铝立方体中的预测波速本别为6279 m/s和6254 m/s.本文的三维声发射源定位方法，并不需要此速度信息，仅是测量查看样品的声速分布，查看样品是否为均匀三维结构.

图5 接收传感器簇中的两个传感器记录的声波信号，Δt是到达时差

图6 铝立方体的声发射源定位实验结果(一).

使用均质的铁长方体进行第二次实验，通过传感器在多个方向上多次测量的铁立方体的速度为5802 m/s，根据公式(11)获得的铁长方体中的预测波速为5986 m/s.同样的方法用时差求得声波传播路径，从而求出三维铁块中声发射源定位预测结果如图8所示.

图7 铝立方体的声发射源定位实验结果(二).

图8 长方体铁的声发射源定位实验结果.

在这两个实验中，由于实验结果是通过一个传感器簇及其对称数据获得的，因此y值始终给出零误差.但是x和z值受测量时间差的误差影响，而x、y、z是可以调换的，所以实验是可信的.以上两个样品的物理实验表明，本文提出的三维结构声发射源定位原理及实验方案，可以达到快速定位三维结构中的声发射源的实验目的.

4 小结

本文提出了一种三维声发射源定位实验的简易实现方法，基于特定观测点间的时差和空间信息，实现快速定位声发射源.定位方法上无需求解复杂的非线性方程组和测知先验的材料属性，不受材料各向异性限制，定位过程清晰简明，帮助学生更好地理解物理问题.硬件上通过实验室常见的示波器、单通道声发射信号采集系统和两个超声波传感器就可以实现，大大降低了实验成本，有利于三维声发射源定位实验的推广和普及.