基于LBP的鲁棒特征提取与匹配方法研究

蔡秀梅，卞静伟，吴成茂，王 妍

1.西安邮电大学 自动化学院，西安710121

2.西安邮电大学 电子工程学院，西安710121

图像匹配技术是图像处理以及计算机领域非常重要的一项技术，目前已在目标识别[1]、图像拼接[2]、三维立体重建以及医学等方面得到了广泛应用[3]。当前常用的匹配算法可分为三大类：基于特征的匹配、基于灰度的匹配和变换域匹配[4-5]。其中基于特征的匹配由于具有对各种变化的鲁棒性强、灵活性好的特点而备受众多学者关注，是目前应用最为广泛的方法之一[6-9]。

1999年，Lowe提出SIFT（Scale-Invariant Feature Transform，SIFT）算法[10]，十多年来，SIFT算法是应用最多的特征匹配算法之一。它具有较好的尺度不变性，以及较强的抗噪声能力和抗干扰能力，但同时存在维数高、时效性差等缺点。因此，为了解决SIFT算法的时效性与维数高的问题，Bay等[11]提出了SURF（Speeded-Up Robust Feature）算法，该算法维数低，时效性也较好，但存在无法保存大量特征点的问题。而Harris算法[12]是基于图像灰度值特征提取方法，它解决了这一问题，同时也克服了时效性以及维数低等不足。近年来，基于机器学习的相关算法也较为流行。例如，cascadeCNN、MTCNN算法等，它们由于算法新颖、结果更准确而更受欢迎，但也有不足，例如它们大多更适于人脸识别，主要识别一些静态物体或有规律运动物体的特征[13]。主要原因在于它们对目标样本集、训练集、测试集进行大量的测试后得到结果，使该类算法存在运算过程繁琐且计算量较大的问题[14]。因此，Harris角点检测算法，相对于SIFT算法、SURF算法、基于机器学习[15]的算法而言，存在可创新性，可改进点较多，计算过程较简单，且对常见图像变换不敏感，易改进且便于结合其他算法，不足在于不具备较好的尺度不变性以及基本的抗噪能力。本文重点是对局部特征角点进行提取与检测，考虑到Harris算法适用于角点特征检测[16]。本文将对Harris算法进行改进，使其具有较好的尺度不变性，同时为了增强Harris算法尺度变换性，本文将鲁棒LBP描述子嵌入Harris角点特征提取方法[17]，增强该算法的稳定性并具有尺度变换不变性；同时，对目前特征匹配算法存在精度低、抗噪性差和适应光照变化能力弱等缺陷进行改进。

因此，本文不仅提出了改进的Harris角点检测方法，而且将它与新构建的鲁棒LBP描述子以及图变换GTM相结合[18]，设计了一类具有较强鲁棒性的图像变换匹配算法。首先，在现有的Harris角点检测算法的基础上，自适应修改自相关矩阵的阈值，增强了Harris算法角点检测能力。其次，利用鲁棒局部旋转不变二进制模式（Local Rotation Invariant Binary Patterns，LRIBP）代替传统LBP描述子，同时对其计算过程进行改进，降低了计算复杂度，增强了稳定性，并将改进的LRIBP用于特征点高效描述。最后，在特征点粗匹配所得结果的基础上引入图变换进行部分特征剔除，经过反复多次迭代实现精确匹配。实验结果表明，本文算法不仅降低了计算时间开销，而且获得了满意的匹配效果。总之，本文算法不仅表现出了良好的匹配性能，而且对尺度变化、旋转变换、噪声干扰、光照变化等均具有一定的鲁棒性和稳定性。

1 相关工作

一般而言，现有大多数特征匹配算法，例如SIFT、SURF、ORB以及基于机器学习的算法，主要重视算法的准确度和实时性[18]。虽然多数算法都具有较高的准确性，但是其稳定性差，算法复杂，且多数算法仅能识别简单图像或满足单一要求，对于复杂图像的匹配不仅准确率低，且稳定性较差。为此，本文提出一种鲁棒LBP算法作为特征点提取的新方法，同时结合Harris角点检测[19]算法，提出新的特征提取与匹配算法，使其克服Harris算法尺度不变性差和鲁棒LBP算法抑噪能力差的缺陷；同时，采用规则分布将特征点为中心的24个邻域像素点及LBP值相结合，构建一个25维特征向量作为特征区域的描述子，不仅降低了算法的复杂度，而且可提高其实时性。最后采用图变换的方法进行误差匹配的剔除，通过自适应设定阈值进行迭代，直至误差匹配点全部剔除。鲁棒LBP特征匹配过程如图1所示。对于特征点匹配部分，使用Harris算法对加入噪声的图片进行特征值检测，然后使用改进的LBP进行特征选择是图像特征匹配的关键步骤，也是匹配正确率的保证。根据不同的特征提取方法，得到需要匹配的特征点进行欧式距离匹配，匹配所得结果再采用GTM算法构建KNN图[20-23]，实现错误匹配点的删除。

图1 鲁棒LBP特征匹配示意图Fig.1 Schematic diagram of robust LBP feature matching

2 实现过程

2.1 改进的Harris特征检测

Harris角点检测算子对图像进行一阶差分，采用自相关函数描述邻域内像素点的灰度变化[24]，并通过高斯滤波降低图像中的噪声干扰[25]。改进后Harris角点检测算子的主要步骤如下：

（1）计算图像I中像素点(x,y)在水平和竖直方向上的度Ix和Iy，计算Ixy=Ix×Iy，即像素点对应位置上的元素积。

（2）图像I与高斯函数进行卷积运算，分别计算G*Ix,G*Iy,G*Ixy,得到像素点(x,y)处的自相关矩阵N，表达式如下：

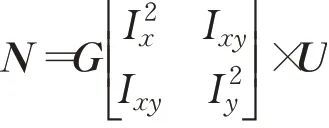
其中，N为自相关矩阵，U为改进设定的阈值，通过U值的改变对待测特征点进行检测，其值根据提取的角点特征密度而定。

（3）计算图像点对应的角点响应函数得到的对应函数响应值[26-27]，如式（1）所示：

其中，det(N)和trace(N)分别是矩阵N的行列式λ1×λ2和迹λ1+λ2,k为常系数，一般取0.04（也可根据特征提取的结果相应改变，直至效果变好，确定系数值）。

（4）在以像素点(x,y)为中心的小邻域内，判断点(x,y)的CRF值是否是该邻域内的极大值，若是，则将其标记为角点；若不是，则判断下一点，并在检测系统中设置循环，当检测到非角点时置0，并重新开始直至所有点全部检测完成。

对传统的Harris角点检测算法进行改进，主要体现在两点：首先是采用3次高斯滤波，增加其抗噪能力，其次设置阈值进行局部角点的去除，改变传统Harris算法存在稳定性差、抗噪能弱的问题。同时由于Harris算法本身不具备较好的尺度不变性，可以结合改进LBP算法进行特征检测与提取，用于提高特征提取与检测的速度以及增加尺度不变性。

2.2 鲁棒性LBP特征描述

2.2.1 LBP算法的扩展

鉴于LBP简单高效的特点，各种扩展LBP的方法层出不穷。目前，主要的扩展方法可归为以下几类：

（1）从邻域拓扑结构角度对LBP进行扩展，提高稳定性。

（2）从降低噪声影响角度对LBP进行扩展，增强抗噪能力。

（3）从降维角度对LBP进行扩展，降低维度，减少算法的复杂度。

（4）从编码方式角度对LBP进行扩展，提高算法的实时性。

（5）从获取旋转不变性角度对LBP进行扩展[28]，提高算法的尺度变化和旋转变换的不变性。

2.2.2改进的中心局部二值模式（鲁棒LBP）

本文提出通过改进邻域拓扑结构对LBP进行扩展，使其对光照变化、噪声干扰以及尺度变化等具有较好的匹配效果，同时减少算法的复杂性，增强算法的鲁棒性。LBP纹理特征提取效果如图2所示。其中图（a）、（b）、（c）、（d）分别是邻域数不变情况下，纹理在原图、半径为2、半径为8、半径为16时的变化；图（e）、（f）、（g）、（h）分别是半径不变情况下，纹理在邻域数为1、邻域数为2、邻域数为8、邻域数为16时的纹理变化。

图2 LBP纹理特征提取Fig.2 LBP texture feature extraction

具体方法步骤如下：

（1）对传统LBP算法进行改进，提出局部旋转不变二进制模式，在一个以特征点为中心的10×10的图像区域内进行特征描述，采用规则分布的，在以特征点为中心的24个像素点及LBP值作为特征区域的24维特征描述符，同时存在两个近似圆的半径为R1=2,R2=4。如图3 所示，该计算方式可以降低特征描述量，同时采用高斯加权对特征邻域内的信息进行加权求值。离特征点近的像素点贡献较大，距离远的贡献小。

图3 子特征点分布Fig.3 Distribution of sub-feature points

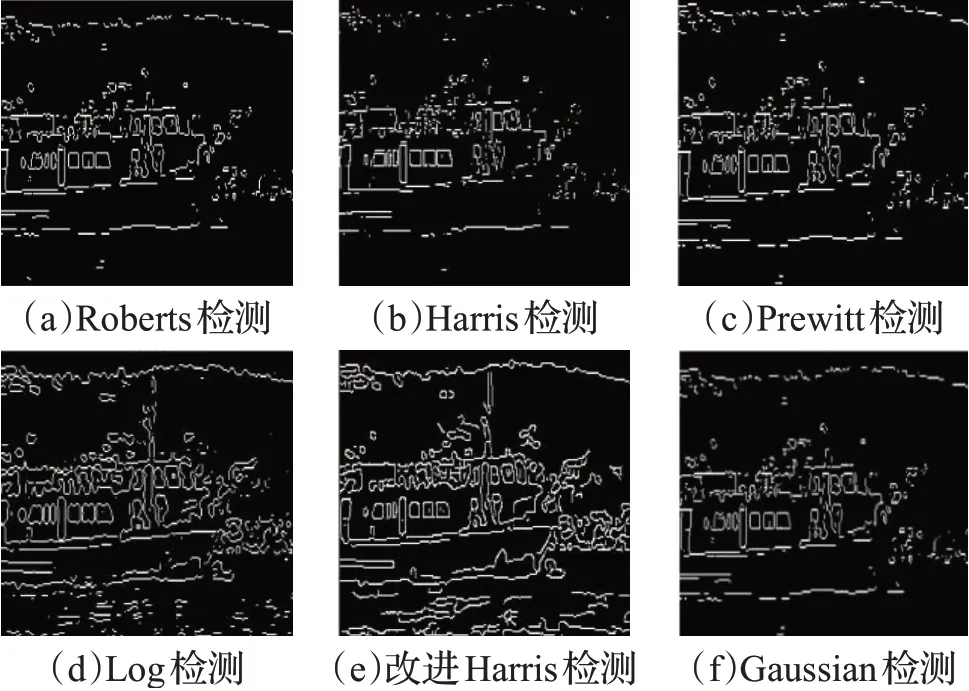
（3）搜索区域估算：设最优的匹配点集合为{

（4）对于局部匹配，匹配区域的半径估算如式（3）、（4）所示：

（5）图2（a）~（d）所示是在邻域数目N（Neighbors）不变的条件下，改变半径，从而使图像的亮度发生变化。通过改变半径R以及邻域数N来使图像的纹理及清晰度发生变化，从而提取和筛选需要的特征。

（6）图2（e）~（h）所示是半径R（Radius）不变，通过改变邻域数，使图像纹理的精细程度得到改正。

2.3 特征匹配

图像检索的匹配策略大致可分为两种，一种是完全匹配，另外一种是相似性匹配。当两幅图像的特征间距离小于某一个阈值时，图像匹配成功，称之为完全匹配。当两幅图像的特征间距离小于或等于某一阈值时，图像匹配成功，称之为相似性匹配。

在基于内容的图像检索中占主导地位的是建立在图像低层视觉特征对比基础上的相似性检索。在提取图像特征后，可采用对应的相似度量策略来进行特征匹配，也就是确定待检索图像同数据库目标图像间的相似性。一个合适的相似性度量方法对图像检索结果影响很大。因此相似性度量方法的好坏会直接影响到图像检索的性能。

2.4 误差匹配剔除

2.4.1误差匹配准则

（1）相似性准则

根据上面系统需求分析，笔者确定该系统的实现软件为客户机/服务器模型，又称为Client/Server体系结构。服务器Server通常采用高性能的工作站或PC小型机，并采用Client/Server架构数据库系统，如Sybase Oracle或SQL Server，负责供多个用户共享其信息和功能。客户端Client部分通常负责执行前台功能，如与用户交互，数据处理等。这种架构由多台计算机构成，它们有机地组合在一起，协同完成整个应用，并达到使系统中的软件、硬件资源得到最大限度的利用。

令ε为相似性阈值，若候选点对(Pi,Qj)的相似性度量Sij<ε，则候选点对(Pi,Qj)将被排除。

（2）相容性准则

相容性Gij表示候选点对(Pi,Qj)和它们的邻近点间的对应水平。令M为相似性阈值，若候选点对(Pi,Qj)的相容性度量Gij

为了有效地识别错误匹配点，本文选择使用相似性准则与相容性准则的方法，达到待匹配误差点去除的目的。因为相似性匹配应用于特征点之间的匹配，通常通过距离或者对比匹配点与待匹配点之间的距离是否最近来判断是否为误差点。虽然过程简单，但存在一定的误差，因此可以先用其进行粗检测，剔除部分不符合的特征点。而相容性更多是应用于图像之间的拼接，优点是误差小，效果较好，能够处理特征不明显的信息，通过识别(Pi,Qj)点的像素对特征邻域内的信息进行加权求值，得到像素值。然后对匹配点与待匹配点进行像素值比对，设置相似性阈值，排除特征不明显的点，且不会丢失多余的信息量。但相容性准则也存在过程复杂、时效性差、仅能处理较小像素点的缺点。为了解决这一不足，本文使用相似性准则与相容性准则相结合的方法进行误差点处理，可以对两者的不足进行互补。如流程图4所示，通过特征检测获得信息量较大的点，并剔除特征不明显的特征点。然后对匹配图与待匹配图之间的特征点进行检测，当满足度量量时，完成误差点剔除，进行下一步。

图4 误差匹配特征点流程图Fig.4 Flow chart of error matching feature points

2.4.2 K最近邻图变换误差剔除法

Aguilar等提出的GTM算法首先根据模板图像与待匹配图像特征点之间一对一的匹配关系构建一个K最近邻图（KNN图），然后对其中的各个顶点进行迭代，达到删除误匹配点的目的。本文将以此为基础，对匹配误差点进行剔除。GTM假设两幅图像之间存在初始匹配点集M={Mi}和Z={Zi},且匹配点集大小都为W，其中M点与Z点是对应的匹配点。该算法主要由两部分组成：

（1）建立KNN图。对M中任意一个匹配点定义一个顶点oi，因此Oi=o1,o2,…,oN，当Mi和Mj的最近邻小于ε，此时存在一个没有定义的边e(i,j)，其中ε为匹配点到顶点oi的中值距离，可以定义为：

得到的点记为QN，则得到所有的匹配点KNN为GN=

（2）删除离群特征。当存在错误匹配时，将错误的匹配点称为离群特征，当两幅图结构不同时，可以采用误差准则来判断是否离群。首先采用相似性准则进行粗判断，将不符合的点剔除，再使用相容性准则对加噪后的像素点进行识别，减小干扰。最后使用三角误差准则进行精准的特征剔除，当时为剔除点，设剔除点为βout，如图4所示，当离群特征点全部剔除后，符合阈值β时，匹配完成，阈值定义为：

3 实验步骤

针对本文建议的鲁棒特征提取与匹配算法，下面给出详细描述过程。

步骤1输入匹配图和待匹配图。

步骤2在匹配图中加入高斯噪声或椒盐噪声（加入高斯和椒盐、光照、尺度以及旋转变换在匹配图和待匹配图中），以增强干扰。

步骤3用Harris角点检测算法进行特征点检测和提取。

步骤4选取相应大小的区域作为特征区域，并确定特征点。

步骤5在区域内对其特征点的像素值求取其LBP特征值。

步骤6对目标特征点采用欧式距离进行匹配。

步骤7进行误差匹配剔除。

步骤8返回步骤6，重新开始进行新一轮迭代，当θ=0时停止。

4 测试结果与性能分析

为了验证本文算法的可行性并检测本文算法的性能，将本文算法与Harris算法、鲁棒LBP算法以及改进的Harris算法进行性能比较，在相同情况下进行数据分析，并分别对其鲁棒性进行验证和分析。同时，对本文算法中的特征匹配所对应的特征值及像素进行细化，以达到精准匹配的目的。

4.1 特征描述与检测分析

为了提高特征匹配的稳定性、抗干扰能力及对尺度和旋转变换性能的稳定性，本文将鲁棒LBP（Robust LBP）和改进的Harris算法相融合来提高匹配结果的稳定性。同时提出并对比六种边缘检测的方法，如图5、图6所示。其中图5是未加噪声的特征图像，图6是加入噪声或光照变化的特征图像。

图5 六种边缘特征的特征点分布Fig.5 Distribution of feature points of six edge features

图6 六种边缘特征的特征点分布（加入噪声）Fig.6 Distribution of feature points of six edge features（adding noise）

如图5所示，分别为Roberts、Harris、Prewitt、Log、改进Harris、Gaussian六种边缘检测结果。通过对比图5（b）、（e）与图6（b）、（e）得知，改进的Harris边缘特征检测比其他五种检测效果好，且特征点分布较为明确，纹理分布清晰，覆盖率较高，检测到的特征点也较多。Roberts、Harris与Prewitt三种特征检测方法，特征分布较为分散，效果较差。Gaussian与Log效果较好，因此对比详细检测数据如表1所示。

由表1数据结果显示，由检测时间、覆盖率以及特征数的比较可知，改进的Harris特征检测方法较其他五种方法更优。

表1 特征检测实验数据结果Table 1 Experimental data results of feature detection

4.2 仿真实验与结果分析

如图7所示，分别为本文算法、鲁棒LBP算法、Harris算法以及改进Harris的匹配结果。采用纹理相同但条件不同的图像对四种算法进行特征匹配，从匹配类型、特征点数以及匹配时间三方面来对比四种算法之间的优缺点。

表2 、表3、表4和图7，分别为本文算法、鲁棒LBP算法、Harris算法以及改进Harris算法的匹配效果与数据测试结果。

表2 特征匹配实验结果（原图）Table 2 Feature matching experiment results（original image）

表3 特征匹配实验结果（加入噪声）Table 3 Feature matching experiment results（adding noise）

表4 特征匹配实验结果（加入噪声+光照）Table 4 Feature matching experiment results（adding noise+light）

为了证实本文算法所具有的鲁棒性和稳定性，分别对图像在噪声、光照、尺度变化和图像变换条件下进行测试。本文分别对177×300大小的图片进行特征匹配，并对本文算法与另外三种对比算法进行对比，并分别从原图、加噪以及加入噪声影响和光照变化影响这三种状况来进行结果与实验的对比分析。如图7所示，验证了四种算法在不同环境下的稳定性。每幅匹配结果均由参考图与待匹配图匹配完成，并分别对其进行尺度变换以及旋转不变性能的检测，在经过8次成功测试后，记录并统计数据，然后求其均值。（1）对比四种算法在原图中的匹配正确率可得，本文算法匹配率最优为98.24%，且检测到的特征点较合适，匹配时间也较短，为3.56 s，可得本文算法最优且达到精准匹配，具有较好的尺度不变性和旋转变化性能。（2）在加入噪声情况下，本文算法正确匹配率97.48%，特征点数为688，匹配时间为4.79 s，均为四种算法中最优结果。（3）当同时加入噪声以及光照条件下，本文算法的正确匹配率为95.31%，较其他三种情况最高，且检测时间最短，匹配效果最清晰，特征检测数最少。综合以上四种算法在相同条件下的对比，可以得出本文算法具有较好的抗噪性、抗光照变化、鲁棒性，以及较好的尺度与旋转变化性能，达到精准匹配和时效性的目的。

图7 四种算法的匹配结果对比Fig.7 Comparison of matching results of four algorithms

4.3 性能对比

本文对Harris算法、鲁棒LBP、改进Harris算法以及本文算法进行性能分析和精准性判断。测试所用的图像经过处理后均符合要求：纹理众多，图像复杂度由低到高，每组图像由匹配图像和待匹配图像组成。为了测试四种算法在各种变化和干扰情况下的匹配性能，所选的图像包含模糊变换（bikes）、尺度和旋转变换（boat）、光照变化匹配性能对比（Leuven1）、算法鲁棒性（Robustness）性能对比等图像变化方式。实验环境为：CPU AMDRyzen5、2.5 GHz，Windows10家庭版，MATLAB-2016A。为了对比上述几类算法的性能，本文采用文献[13]的查准率-查错率recall和1-precision对应的曲线作为评估标准。recall和1-precision曲线定义如下：

四种算法对模糊图像和噪声的匹配结果如图8（a）所示，因为本文算法具有较强的抗干扰能力，所以对模糊变换性能的适应能力比其他三种算法更好（由图8（a）可知）。差错率在0~0.6之间时本文算法的匹配性能更好，整体来看本文算法对模糊图像以及噪声的匹配效果更好，优于Harris和鲁棒LBP算法。图8（b）是对尺度和旋转变换图像的匹配结果对比，可以看出，差错率在0~0.25之间时，本文算法和鲁棒LBP算法的查准率基本相差不大，这是由于本文提出的鲁棒LBP算法的尺度和旋转变化性能自身就很强。但差错率在0.3~0.7之间时，本文算法的查准率明显优于其他三种算法，这是因为本文主要是针对抗干扰提出的方法，所以相比于匹配特征的像素要低得多。在差错率较高的地方有明显的匹配效果，同时相比于其他三种算法，本文算法的抗干扰能力更强，效果更优。具体结果如表5所示，本文算法更优。

图8 三种方法的匹配性能对比Fig.8 Comparison of matching performance of three methods

表5 三种算法性能对比Table 5 Performance comparison of three algorithms

5 结束语

针对SIFT算法计算复杂度高、实时性较差的问题，本文提出一种改进的Harris算法结合LBP的方法，旨在降低计算复杂度和解决实时性差的问题。并提出了基于局部的中心对称局部二值模式和图变换相结合的匹配算法，分别对图像在噪声、光照以及旋转等条件影响下进行匹配。该算法采用子特征点稀疏计算特征区域的LRLBP值，并采用局部不变坐标系，避免主方向估计和图像的旋转，在粗匹配后采用GTM算法对匹配点进行剔除，提高了算法的准确率、稳定性和尺度不变性。实验表明，本文算法计算复杂度低，鲁棒性好，在确保匹配效果的前提下，算法的运算速度提高，并且匹配效果以及稳定性明显增强。

本文算法较Harris和鲁棒LBP算法表现出更好的稳定性以及匹配准确率，主要原因是：（1）在特征提取方面本文采用改进的Harris角点检测算法和鲁棒LBP进行特征的提取与检测，通过改变阈值进行特征提取，减少了信息量较少的特征点提取。（2）通过欧式距离进行特征匹配，然后通过KNN进行误差匹配点的剔除。

本文算法鲁棒性好，主要原因有：（1）利用局部二值法和图变换的匹配算法相结合进行特征检测与提取，从而提高了在光照、噪声等影响下，对特征进行检测与提取的稳定性。（2）利用欧氏距离进行特征匹配，通过GTM以及KNN进行误差匹配的剔除，达到精准匹配的目的。

与Harris和鲁棒LBP算法对比的测试中，本文算法在光照以及噪声的情况下，表现出明显的鲁棒性与稳定性；在尺度与旋转等情况下也表现出了较强的健壮性。下一步的研究方向主要是对特定物体的特征进行提取与匹配，并提高其鲁棒性。