结合模拟退火与规则约简的模糊系统优化方法
童文林,陈德旺,黄允浒,吕宜生
1.福州大学 数学与计算机科学学院,福州350108
2.福州大学 智慧地铁福建省高校重点实验室,福州350108
3.中国科学院 自动化研究所 复杂系统管理与控制国家重点实验室,北京100190
模糊理论自诞生之日起,就一直处在各派的激烈竞争中,经历了跌宕起伏的2次兴起和3次衰落的发展历程[1],但其理论研究仍然不够成熟[2-3]。它是一种可解释性很强的人工智能方法。对于神经网络而言,即使是专家也难以解释和理解参数的意义[4]。而模糊系统由一系列模糊IF-THEN规则构成,其结构和参数可以用该规则来解释,具备快速、灵活性强、易于理解的特点,但其缺点是自学习能力差,模型精度不高。
王立新与Mendel提出了经典的模糊算法WM[5]。该算法从样本数据中通过自学习构建模糊系统,具有简单实用的特点,并且在领域内被广泛地应用。但WM方法中一条规则仅由一条数据产生,使得通过WM方法构造的模糊系统缺乏良好的完备性以及鲁棒性。因此,王立新对WM方法进行改进[6],定义了冲突规则以及相邻规则。通过多条数据选举产生一条规则,对于完备规则库中无法从数据中提取的规则,通过相邻规则外推得到,改善了其完备性不足的问题。但WM方法主要关注于如何从数据中学习模糊系统,对学习后的模糊系统关注不足,导致其鲁棒性问题仍然没有得到很好的解决。
针对这些问题,一些研究者提出了基于神经网络的方法[7]、模糊聚类[8]、基于全局优化的模糊系统[9]、基于神经网络、模糊系统和遗传算法[10]三者相结合的方法以及许多改进的模糊算法以及模糊优化算法,例如Garg等[11]、Wu等[12]以及Shi等[13]提出的优化方法。上述算法在一些应用中取得了较好的效果,但是对于模糊集合的划分个数、隶属度函数参数的选取缺乏有效的指导[14],可解释性仍然有待提高。
因此,如何在模糊建模过程中避免算法效率下降以及兼顾完备性、鲁棒性的同时,提高模糊系统的可解释性仍然是亟待解决的问题。基于以上分析,本文从模糊规则提取与约简以及模糊系统结构优化即隶属函数参数优化三方面进行考虑,同时结合模拟退火(Simulated Annealing,SA)优化算法及模糊支持度(Degree of Support,SD)的特点,提出基于模拟退火与支持度规则约简的模糊系统优化方法SSF。
1 模糊系统理论分析
Mamdani模糊系统(也称为Zadeh模糊系统)规则表示形式如式(1)所示:前件IF部分及后件THEN部分均使用模糊集合表示。
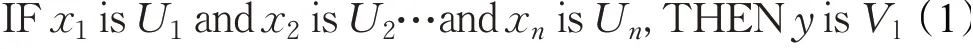
其中U1,U2,…,Un与V1分别为输入与输出空间上的模糊集合。
图1 展示了由模糊化、模糊规则库、推理机和去模糊化四部分组成为的Mamdani模糊系统。其中模糊化把每个输入映射成模糊集,推理机基于规则库进行推理来得到一个新的模糊集,通过去模糊化把模糊集映射成一个数值化输出。模糊规则库作为模糊系统的核心部分,其组成除了模糊规则表示形式,还包括模糊集合的隶属度函数表示形式[15]。

图1 Mamdani模糊系统示意图Fig.1 Schematic diagram of Mamdani fuzzy system
本文隶属度函数使用三角形隶属度函数,其定义如式(2)所示:

其中,σ表示三角形隶属函数的偏差,yc表示三角形隶属函数的中心值,y表示输入值。
2 本文算法
2.1 模糊规则提取
对于模糊规则的提取,本文采用以完备的模糊规则库为基础,分别确定规则前件与后件的方式,以保证模糊规则的完备性。首先对输入空间进行划分,在划分且为每一维输入空间分别分配mi个(i为数据维度)模糊集合后,则可以确定一个完备的模糊规则库所包含的模糊规则数目为∏mi,以及每一条规则的前件部分均由每一维上的模糊集合组合而成,具有式(1)前件的形式。对于规则后件的确定,利用所有输入数据,根据数据对规则的贡献程度来确定。
从数据挖掘的角度看,每一个样本数据对完备的模糊规则库中的每一条规则都是有贡献的,本文用数据在模糊规则前件上的隶属度来描述数据对规则的贡献程度。假设有n条样本数据且完备的模糊规则库中包含N条模糊规则,那么C(i,j)表示数据i对规则j的贡献度(i≤n,j≤N),如表1所示。

表1 数据贡献度Table 1 Data contribution
将规则前件看作规则包含的n个模糊集合的笛卡儿积,例如有一条规则具有如下前件形式:

其中,⊗表示一种t范数。爱因斯坦积与代数积均具有有界性、交换性、非减性以及结合性。同时代数积具有计算及应用简单的特点,而爱因斯坦积通过一个与自变量相关的因子在一定程度上对输出值进行修正。因此本文选择这两种t范数:
(1)爱因斯坦积

(2)代数积

假设一个二维输入单输出且满足y=X1+X2的模拟样本数据,如表2所示。
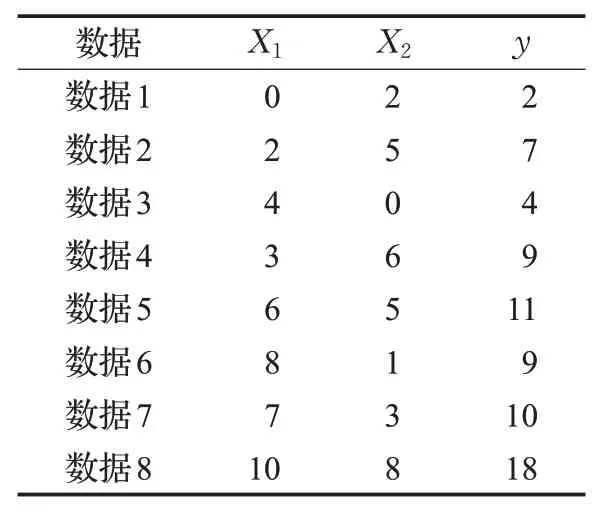
表2 模拟样本数据Table 2 Simulation sample data
将每一维输入空间(X1:[0,10],X2:[0,8])划分并分别分配3个模糊集合,X1空间上的模糊集合为X2空间上的模糊集合为,如图2所示。
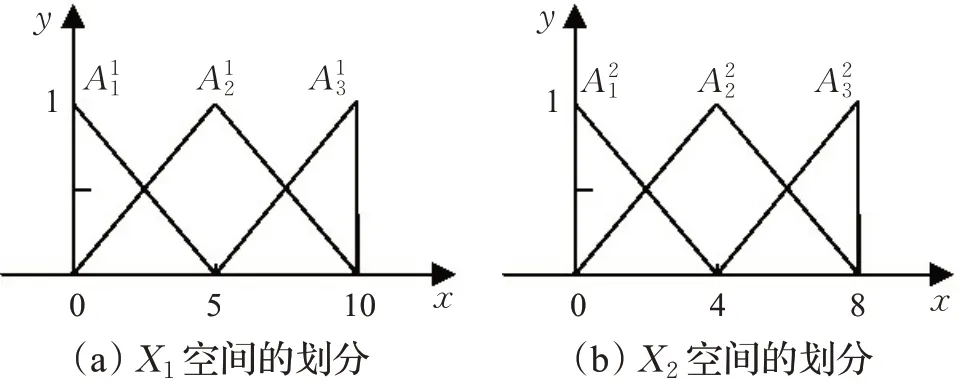
图2 输入空间划分示意图Fig.2 Schematic diagram of input space division
因此,根据式(2)可以得到每一个模糊集合上隶属度的计算公式,如式(6)~式(11)所示:

那么就可以确定一个完备的模糊规则库将包含9(3×3)条规则,其规则形式如下所示:

其中B1,B2,…,B9为规则后件待确定的模糊集合。根据式(3)、式(4)和式(5),可以计算得到样本数据在规则上的隶属度。以数据1对规则1的贡献度C(1,1)计算为例,根据式(3),首先计算出数据1(0,2)在规则1上的隶属度:

其中⊗运算以代数积为例,则:

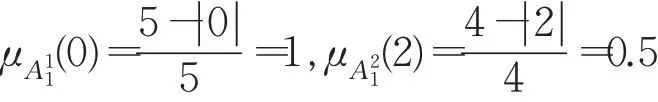
同样的,可求得数据1对规则1至规则9的贡献度C(1,j);数据2对规则1至规则9的贡献度C(2,j);数据3对规则1至规则9的贡献度C(3,j);数据4对规则1至规则9的贡献度C(4,j);其中j=1,2,…,9。经过计算,表2对应的数据贡献度表如表3所示。

表3 样本数据贡献度Table 3 Sample data contribution
得到每一条数据对每一条规则的贡献度后,以此作为权重,计算规则j输出部分模糊集合的中心值及偏差σj,从而确定所有的规则,如式(12)和式(13)所示:

2.2 模糊规则约简
当前的研究主要集中在如何提高模糊系统的精度,而对于学习后的模糊系统的规则数关注不足,影响了模糊系统的可解释性。因此,适当约简系统规则对提高模糊系统的可解释性显得尤为重要。完备的模糊规则库中的一些规则相对训练数据而言是冗余的,本文通过支持度来描述规则是否冗余。支持度SD定义如下:
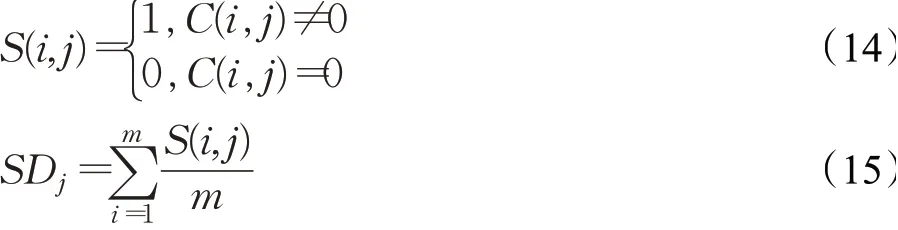
其中,S(i,j)表示数据i在规则j上的指示函数值,m为样本数,SDj为第j条规则的支持度。当规则j的支持度SDj小于规则约简阈值时,规则j被认为是冗余的,将规则j从完备的模糊规则库中删除;反之,当规则j具有足够的支持度时,将其保留。
在2.1节例子的基础上,对表3根据指示函数公式(14)以及支持度计算公式(15)进行处理,可以得到规则1至规则9的支持度,如表4所示。

表4 规则支持度Table 4 Rule support
设定规则约简阈值为0.3,那么规则1、规则3以及规则9的支持度低于该阈值,则将这些规则从完备的模糊规则库中删除。因此从样本数据中获取的模糊规则库中包含规则2、规则4、规则5、规则6、规则7以及规则8。
2.3 模糊系统结构优化
在提取并约简规则后,初始的模糊系统已经构建完毕。但是由于模糊集合的分配与输入空间的划分往往是根据经验进行的,带有很强的主观性,这样的模糊系统结构往往难以满足数据的要求。因此根据模拟退火算法对初始的模糊系统结构进行调整,使模糊系统的结构更加适应数据。
模拟退火算法[16]在解空间搜索时采用Metropolis准则,以一定的概率接受比当前解更差的解,从而能够跳出局部最优,得到全局最优。该算法从起始温度以及初始解开始,在当前温度下为当前解加入扰动后产生新解以搜索更优的解。当在当前温度下达到一定搜索次数时,通过降温系数降低当前温度继续搜索。温度的降低也将导致对更差解的接受概率逐渐降低,直到温度降低到停止温度时得到最终解。本文隶属函数选择三角形隶属函数,包括left、center和right三个分段点。将系统中包含的所有模糊集合的中心点center组成初始解向量进行搜索。每一次搜索都为当前解增加扰动以产生新解,也就意味着新解对应的模糊集合的中心点相较于当前解对应的模糊集合的中心点发生了改变,为了保证模糊集合重叠的特性,需要同步地调整新解对应的模糊集合的left和right点:将新解对应的所有模糊集合的left点修改为前一个模糊集合的center点,right点修改为后一个模糊集合的center点。
SA算法使用Metropolis准则时,根据当前解与新解在目标函数上的差值决定是否更新当前解为新解。对模糊系统结构参数优化是为了提高模糊系统的精度,因此本文将训练集上的均方误差(MSE)作为搜索过程中的目标函数,如式(16)所示。对于新解而言,用于预测的模糊规则库有两种选择:一种是使用在初始解条件下提取的模糊规则;另一种是利用新解重新提取模糊规则。

其中,ŷk、yk分别为预测值和真实值。ŷk是在由单值模糊化、乘积运算、加权平均反模糊化得到的模型上预测的结果,如式(17)所示:

在搜索新解的过程中,解向量中每一维的解空间在当前解更新后都会发生变化,而在当前解的基础上增加一个受温度参数影响的随机数来增加扰动也会变得难以控制。因此通过在解向量中每一维的搜索范围内随机选取一个值作为新解的每一维实现增加扰动产生新解。同时,解向量中每一维的搜索范围将受到温度的影响:随着温度的降低,解向量中每一维的搜索范围以缩减系数β进行收缩。缩减系数的定义如式(18)所示:

那么解向量中每一维的搜索范围经过缩减后的左、右边界点分别如式(19)和式(20)所示:

其中,left、center和right分别表示解向量对应模糊集合的左边界点、中心点和右边界点,maxT表示初始温度,T表示当前温度。
当温度降低至停止温度时,搜索结束,将退火过程中的最优解作为最终解,模糊系统的结构参数调优完成,最终的模糊系统构造完毕。
3 算法实现及分析
本文的模糊系统建模及优化流程如图3所示。

图3 模糊系统建模及优化流程Fig.3 Fuzzy system modeling and optimization process
3.1 实现步骤
步骤1将导入的数据集进行归一化处理,并划分为训练集Dtrain和测试集Dtest。
步骤2将输入空间进行等分划分,并为每一个子空间分配模糊集合。根据分配的模糊集合确定所有规则的前件。
步骤3计算所有样本数据对完备模糊规则库中所有规则的贡献程度。根据式(14)和式(15)计算每条规则的支持度,并设定规则约简阈值删除冗余规则。
步骤4根据式(12)和式(13)确定模糊规则库中规则后件部分的模糊集合。
步骤5设定模拟退火算法超参数:起始温度maxT、停止温度minT、每一温度下的搜索次数n以及降温系数q。选取初始解,利用SA算法对模糊系统的隶属函数的参数进行优化,调整模糊系统结构。
步骤6最终的模糊系统构造完毕,将测试集数据Dtest输入此模糊系统进行预测,得到预测结果。
同样地,利用表2的模拟数据对本文算法进一步介绍。步骤1是数据预处理的过程,步骤2及步骤3已经分别在前文第2.1节以及第2.2节叙述,因此不在此处赘述。经过步骤3约简规则后,从样本数据中确定了模糊规则库中包含规则2、规则4、规则5、规则6、规则7以及规则8。接着执行步骤4,以规则2为例确定其后件。根据式(12)和式(13),可以分别得到其后件模糊集合的中心点及偏差:

因此根据式(2)得到规则2后件的模糊集合如下式所示:

同样地,其余规则的后件部分模糊集合均可确定。所有规则后件部分确定后,即可得到模糊规则库。
在提取并约简模糊规则后执行步骤4,假设maxT=100,minT=1,q=0.9,n=20。初始时,模糊集合的中心点分别为0,5,10,0,4,8,因此算法的初始解x0=[0,5,10,0,4,8]。从初始解开始搜索,假设经过第一次搜索后产生的新解为x1=[2,4,8,2,6,7],表示新解对应的模糊集合的中心点分别为2,4,8,2,6,7,那么需要同步地调整新解中每个模糊集合的左边界点为前一个模糊集合的中心点,右边界点为后一个模糊集合的中心点。模糊集合调整前后示意图如图4、图5所示,其中黑色曲线表示当前解x0所对应的模糊集合,蓝色曲线表示新解x1所对应的模糊集合。
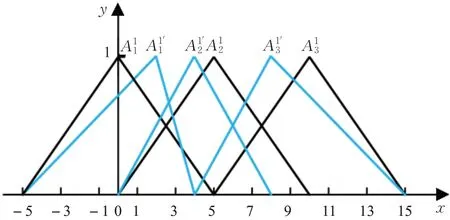
图4 X1输入空间模糊集合调整对比图Fig.4 Comparison diagram of fuzzy set adjustment in X1 input space
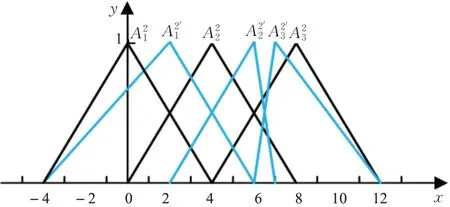
图5 X2输入空间模糊集合调整对比图Fig.5 Comparison diagram of fuzzy set adjustment in X2 input space
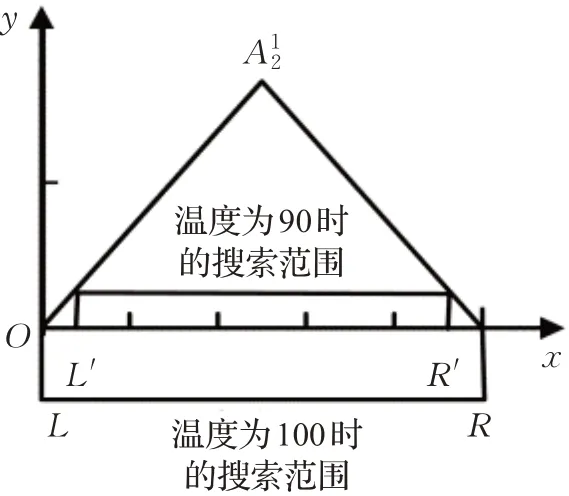
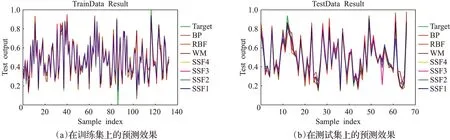
接着根据式(17)分别使用x0对应模糊集合以及x1对应模糊集合对测试集进行预测。对于x1而言,若选择重新提取规则,则执行步骤3、步骤4后再进行预测;否则使用初始解条件下提取的模糊规则进行预测。预测完成后,根据式(16)分别计算当前解的目标函数值f,以及新解的目标函数值f′,即二者在测试集上的均方误差。根据Metropolis准则决定是否接受新解,当f′ 对当前解更新完成后,进行新的搜索。在温度为100的条件下进行20次搜索后,根据T′=q×T降低当前温度为90,同时根据式(18)、(19)、(20)缩小当前温度下新解的搜索范围。在温度为100时: 解向量中每一维的搜索范围为[L,R],即每一维对应的模糊集合的左右边界点之间。在温度为90时: 因此对应的每一维的搜索范围在[L′,R′]。相较于温度为100时,搜索范围缩减了10%,意味着减少了对较差解的搜索,更偏向于较优解。以温度为100时和温度为90时,解向量第二维即集合中心点的搜索范围进行对比,如图6所示。 图6 搜索范围对比图Fig.6 Comparison of search ranges 如此循环搜索,当温度降低到停止温度minT且搜索完成时,选择退火过程中的最优解作为模糊系统隶属度函数参数的解,完成系统结构的优化。至此,模糊系统构造完毕,可执行步骤6对输入数据进行预测。 在实现过程中,提取与约简规则时需要遍历所有样本数据和模糊规则以及存储样本数据对完备模糊规则支持度,因此其时间、空间复杂度均为O(n×N),其中n为样本数据量,N为完备模糊规则库中的规则数。而在优化过程中仅需O(1)复杂度存储SA算法的超参数,需要O(T×C)时间复杂度,其中T为搜索新解的温度个数,C表示每个温度下的搜索次数。整个模糊系统的参数包括输入部分模糊集合以及输出部分模糊集合,其复杂度为O(M+K),其中M为输入空间上划分的模糊集合个数,k为提取约简后的规则量。因为O(1)≤O(M+K)≤O(n×N),所以该算法的空间复杂度为O(n×N),时间复杂度为O(n×N+T×C)。从以上分析看,时间复杂度相对较高,这是用模拟退火算法提高精度所付出的代价,因此降低时间复杂度将成为日后的一个研究重点。 为了验证本文算法的有效性,将t范数使用式(4)爱因斯坦积且在SA中对新解重新提取模糊规则库的算法命名为SSF1;将t范数使用式(4)爱因斯坦积且在SA不对新解重新提取模糊规则库的算法命名为SSF2;将t范数使用式(5)代数积且在SA中对新解重新提取模糊规则库的算法命名为SSF3;将t范数使用式(5)代数积且在SA中不对新解重新提取模糊规则库的算法命名为SSF4。同时引入了BP算法、RBF算法和WM算法进行比较分析。将MSE(式(16))与R2作为客观评价标准。 本文在3个数据集上验证提出的算法,所有数据集均选自机器学习库UCI Machine Learning Repository。各数据集的特征总结如表5所示。 表5 数据集特征总结Table 5 Summary of data set characteristics 图7 展示了各算法在Adv数据集的训练集、测试集上的预测效果。表6、表7分别展示了各算法在训练集和测试集上各项评价指标值。 从表6、表7可以看出,SSF1算法在各项评价指标上都表现得最佳,尤其在MSE与R2指标上,占了绝对优势。结合图7和表7,SSF算法对样本数据的学习能力比BP、RBF以及WM算法都更强。而从图7(b)和表7可以看出,SSF1、SSF2有更好的泛化能力。与WM算法相比,SSF算法在规则数目上均比WM算法的少,可解释性得到提高。SSF1的规则数约是WM的一半,可解释性最好。 表6 各算法在训练集上的各项评价指标值(Adv数据集)Table 6 Evaluation index values of each algorithm on training set(Adv data set) 表7 各算法在测试集上的各项评价指标值(Adv数据集)Table 7 Evaluation index values of each algorithm on test set(Adv data set) 图7 各算法在Adv数据集上的预测效果Fig.7 Prediction results of each algorithm on Adv data set 图8 展示了各算法在DJ数据集的训练集及测试集上的预测效果。表8、表9分别展示了各个算法在训练集和测试集上各项评价指标值。 表8 各算法在训练集上的各项评价指标值(DJ数据集)Table 8 Evaluation index values of each algorithm on training set(DJ data set) 表9 各算法在测试集上的各项评价指标值(DJ数据集)Table 9 Evaluation index values of each algorithm on test set(DJ data set) 图8 各算法在DJ数据集上的预测效果Fig.8 Prediction results of each algorithm on DJ data set 在DJ数据集上,SSF1算法在训练集、测试集中同样表现出良好的性能,在误差以及模型的解释能力上比传统的BP算法、RBF算法以及WM方法都要更好。在规则数目上,SSF1与SSF3分别占WM算法的29.3%与34.6%,SSF2与SSF4的规则数分别占WM算法的56%。可以明显看出,基于SSF的四种算法的规则数显著下降,可解释性进一步提高。 图9 展示了各算法在Rev数据集的训练集、测试集上的预测效果。表10、表11分别展示了各算法在训练集和测试集上的各项评价指标值。 表10 各算法在训练集上的各项评价指标值(Rev数据集)Table 10 Evaluation index values of each algorithm on training set(Rev data set) 表11 各算法在测试集上的各项评价指标值(Rev数据集)Table 11 Evaluation index values of each algorithm on test set(Rev data set) 图9 各算法在Rev数据集上的预测效果Fig.9 Prediction results of each algorithm on Rev data set 从表10可以看出,SSF算法在各项指标上均表现得比其他算法更好。其中SSF3在训练集上的各项指标居于首位,表现出明显的优势。从表11可以看出,SSF1的误差最小,精度最高且对模型的解释能力表现得更好。从规则数目上看,SSF3规则数最少,可解释性最好。 通过实验可以看出,SSF算法在实际回归预测问题中具有一定的可行性以及较好的性能。与一些经典算法相比,SSF1及SSF3算法在精度和可解释性上具有明显的优势: (1)SSF算法以完备的模糊规则库为基础,依据所有数据对规则的贡献程度参与模糊规则库中规则的生成,并通过模糊规则的支持度对冗余的规则进行约简,提高了模型的可解释性。 (2)通过模拟退火算法对模糊集合的结构参数进行调整,克服人工经验的主观性,使模糊系统更加适应数据,增强了泛化能力,提高了预测精度。 当前优化的模糊系统在高维数据中的表现还有待提高。在今后的工作中,将把机器学习中的一些技巧应用到模糊系统构造及优化中,并考虑应用于深度模型中,以适应高维数据的要求,进一步提高模糊系统处理实际问题的能力。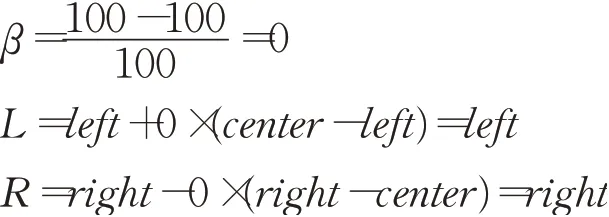
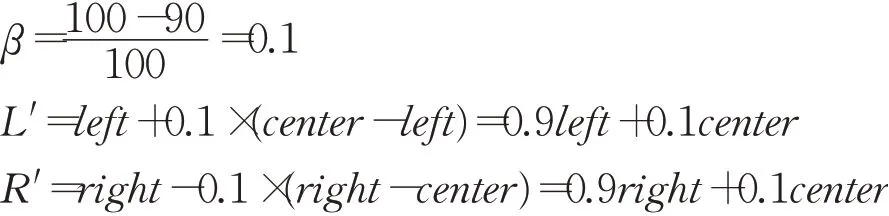
3.2 算法复杂度分析
4 实验结果与分析

4.1 数据集描述

4.2 Adv数据集应用


4.3 DJ数据集应用



4.4 Rev数据集应用



5 结论与展望

