k元n方体网络的子网络可靠性
冯 凯,李 婧
山西大学 计算机与信息技术学院,太原030006
随着并行计算机系统规模的不断增大,系统功能的实现越来越依赖于系统元件之间支撑通信和数据交互的连接模式(即系统的互连网络,其中的每个顶点对应一个处理器,每条边对应一对处理器之间的一条直接通信线路)。以具有优良性能的互连网络为底层拓扑结构设计高性能并行计算机系统已经成为高性能计算领域的一个发展趋势[1]。人们往往选用具有递归结构(即高维的网络可以被划分为一些独立的低维的子网络,并且这些子网络与原网络具有相同的拓扑性质)的互连网络来构建并行计算机系统。一方面,这类网络可以通过特定的机制指派各个子网络完成用户任务的不同部分,从而有效地利用系统资源;另一方面,这类网络便于在原有基础上进行扩容和升级,并且能够保持原网络的良好性能。当基于递归互连网络构建的并行计算机系统中有故障发生时,系统互连网络关于其子网络的保持能力对系统实际应用至关重要。在此背景下,递归互连网络的子网络可靠性得到了学者们的关注[2-5]。Abraham和Padmanabhan[2]对n维超立方体的子网络可靠性进行了研究,分别在不同故障模型下给出了子超立方体保持无故障状态的平均失效时间的估计值。受此启发,Fitzgerald等[3]分别在不同故障模型下基于固定划分模式得出了n维星图网络中不同数目的(n-1)维星图子网络保持无故障状态的平均失效时间,并基于灵活划分模式对这一子网络可靠性评估参数进行了估算。最近,文献[4]和文献[5]分别对(n,k)-星图网络和DCell数据中心网络中不同数目的某一规模子网络保持无故障状态的平均失效时间也进行了分析。
k元n方体网络是一类著名递归互连网络,诸多基于k元n方体网络构建的并行计算机系统已经问世,如Cray T3E[6]、IBM Blue Gene[7]等。近年来,k元n方体网络的拓扑性质得到了广泛的研究[8-14]。针对k为奇数的k元n方体网络,文献[9]在点故障模型下研究了使得k元n方体网络中不存在k元(n-m)方体子网络(0≤m≤n-1)的最小的点故障数,并构建出与任意规模子网络一一对应的符号化表示。随后,文献[13]基于概率故障模型给出了k为奇数的k元n方体网络中存在k元(n-1)方体子网络的概率估计,文献[14]在点故障模型下分析了k为奇数的k元n方体网络中不同数目的k元(n-1)方体子网络保持无故障状态的平均失效时间。
在实际中,许多并行计算机系统可以利用故障诊断算法快速判断出发生故障的处理器并及时进行维修和更换,而处理器之间的通信线路可能由于物理损坏、电磁干扰、人为损坏等因素产生故障且无法得到及时修复(由于系统的处理器对之间大都不存在重复的直接通信线路,不同处理器对之间的通信线路通常可以看作是没有关联的)。基于这一考虑,本文将在边故障模型下(假定互连网络中的顶点不会发生故障,各条边发生故障是相互独立的,且边的故障率是不变的),对k为奇数的k元n方体网络中不同数目的k元(n-1)方体子网络保持无故障状态的平均失效时间进行估计,这一研究可以帮助工程师更加全面地了解k元n方体网络中不同数目的k元(n-1)方体子网络存在性的保持能力。
1 基本概念与性质
k元n方体(k≥2,n≥1为整数)记为,是一个具有kn个顶点的无向简单图。的任一顶点可表示为u=u0u1…un-1,其中对于任意的整数i(0≤i≤n-1)均有ui∈{0,1,…,k-1}。两个顶点u=u0u1…un-1和v=v0v1…vn-1相邻当且仅当存在j∈{0,1,…,n-1}使得uj=vj±1(modk)且对于任意的l∈{0,1,…,n-1}{j}均有ul=vl,这样的一条边(u,v)称为中的一条j维边。容易得出,当k≥3时共有nkn条边,且j维边的数目为kn,其中j∈{0,1,…,n-1}。
性质1[9]中共有nk个不同的子网络。
给定任一整数d∈{0,1,…,n-1},可以将沿第d维划分为k个不相交的子网络其中Hd,i为中由点集导出的子图,这里i∈{0,1,…,k-1}。结合性质1可知,当k≥3为奇数时,中所有不同的子网络恰好是由沿不同维划分得出的。在无特殊说明的情况下,假定下文中出现的均满足k≥3为奇数。
在介绍主要结果之前,先引入一些基本概念和标记(见表1)。对于文中其他未加定义而被使用的图论术语和记号参见文献[15]。

表1 主要符号及含义Table 1 Main symbols and meanings
2 主要结果
2.1 固定划分模式下Ti的计算
选定d∈{0,1,…,n-1},可以将沿第d维划分为k个不相交的子网络基于这一固定划分模式,下面通过计算Ti来评估中不相交的子网络的可靠性。
由R*(t)和T*的定义可知,中所有故障边均位于i个子网络中时中显然有k-i个子网络保持无故障状态,故对于任意的0≤i≤k-1有
因此,为了计算固定划分模式下T*和Ti(0≤i≤k-1)的值,首先需要厘清S*,S0,S1,…,Sk之间的状态转换关系。
基于上述分析可知,当t=0时,P*(0)=1且对于任意的0≤l≤k有Pl(0)=0;当t=∞时,P*(∞)=0,Pk(∞)=1且对于任意的0≤l≤k-1有Pl(∞)=0;P*(t),P0(t),P1(t),…,Pk(t)之间的相互关系可表示为:

其中2≤i≤k。
进一步地,有如下结论成立。
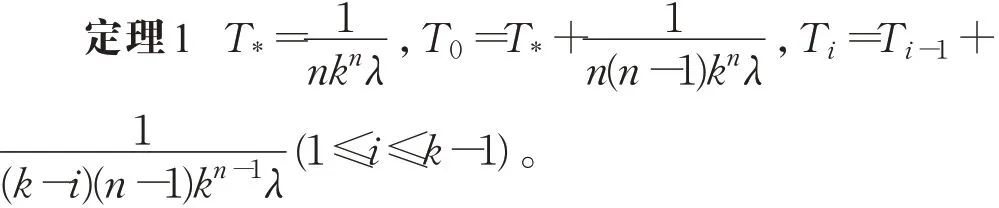
证明由r0)dt。结合P*(0)=1求解可得从 而 可 知,
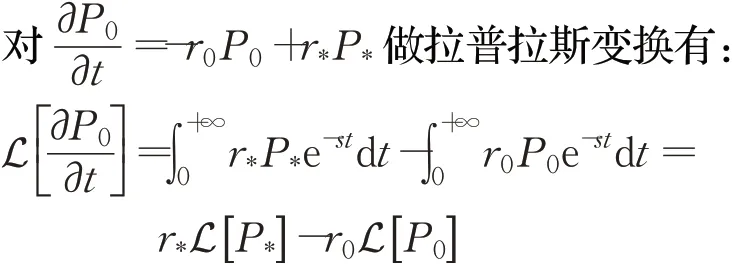
注意到

由P0(0)=0可知:
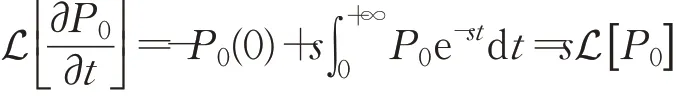
令r=nknλ,则P*(t)=e-rt。对P*(t)=e-rt做拉普拉斯变换可知:



定理1证毕。
例1选取k∈{5,7},n∈{4,5}。在固定划分模式下,不同规模的的Ti的值如表2所示,其中中边的故障率为λ=10-7/h。
表2 固定划分模式下的Ti的值Table 2 Values of Ti in under fixed partition pattern
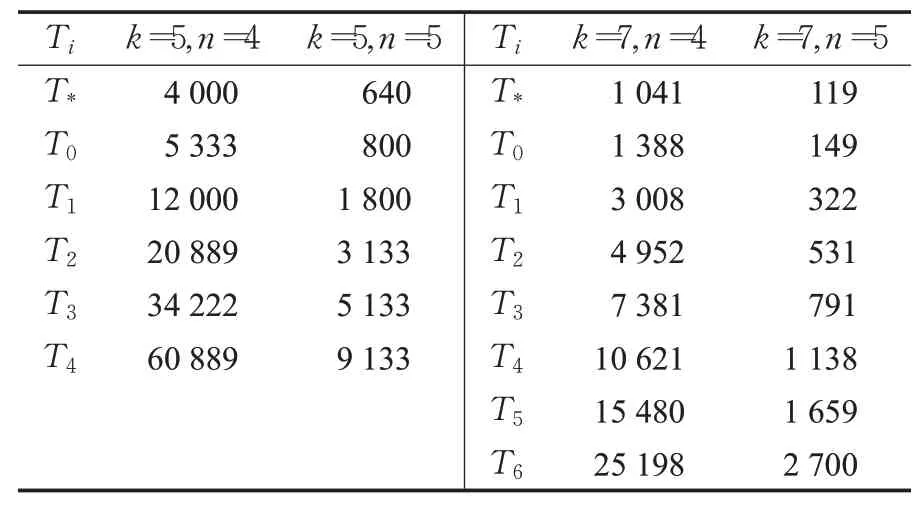
表2 固定划分模式下的Ti的值Table 2 Values of Ti in under fixed partition pattern
?
2.2 灵活划分模式下Ti的计算
注意到,对于任意的d∈{0,1,…,n-1},可以将沿第d维划分为k个子网络。若首条故障边为l维边,那么将沿第l维进行划分(称这种划分模式为灵活划分模式),这样得到的k个子网络均不会被首条故障边所破坏。这意味着,在灵活划分模式下,若处于状态S*,首条故障边不会导致状态S*转换为状态S1。本节将证明灵活划分模式下Ti的值相比固定划分模式下这一参数的值有所增加。为了区分不同划分模式下Ti的计算公式,记灵活划分模式下Ti的值为
令w*=nknλ,wi=(k-i)(n-1)kn-1λ(0≤i≤k)。此时S*,S0,S1,…,Sk的状态转换图如图2所示。

图2 灵活划分模式下S*,S0,S1,…,Sk的状态转换图Fig.2 State transition diagram of S*,S0,S1,…,Sk under flexible partition pattern
基于上述分析可知,当t=0时,P*(0)=1且对于任意 的0≤l≤k有Pl(0)=0;当t=∞时,P*(∞)=0,Pk(∞)=1且对于任意的0≤l≤k-1有Pl(∞)=0;P*(t),P0(t),P1(t),…,Pk(t)之间的相互关系可表示为:
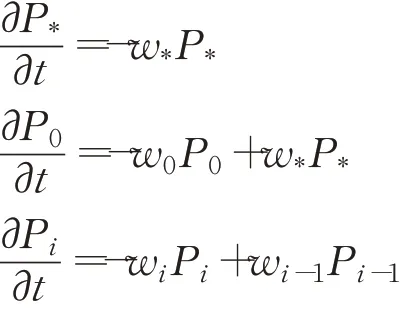
其中1≤i≤k。
采用类似于定理1的证明,可得出以下结论。
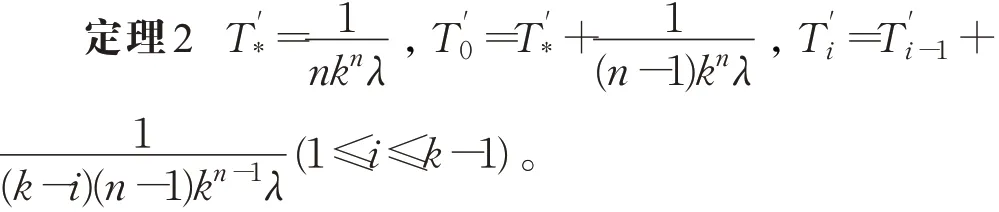
可以看出,相比固定划分模式,灵活划分模式下S*,S0,S1,…,Sk之间的状态转换关系发生了改变,这导致不同划分模式下得出的不同数目的Qkn-1子网络保持无故障状态的平均失效时间的计算公式是不同的。

例2选取k∈{5,7},n∈{4,5}。在灵活划分模式下,不同规模的的值如表3所示,其中中边的故障率为λ=10-7/h。
表3 灵活划分模式下的值Table 3 Values of under flexible partition pattern
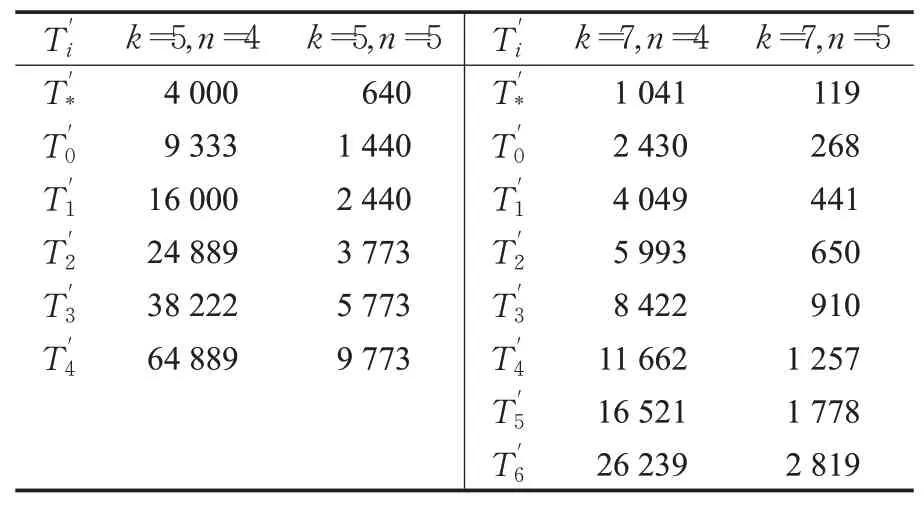
表3 灵活划分模式下的值Table 3 Values of under flexible partition pattern
?
3 仿真分析
为了验证不同划分模式下理论结果的精确性,本文采用蒙特卡洛仿真来评估边故障模型下中不相交的子网络的可靠性。选取不同规模的n∈{4,5})为实验对象。假定中边的可靠性是独立同分布的,且均服从故障率为λ(λ=10-7/h)的指数分布。在任意时刻t,中边的可靠性为p(t)=e-λt。令f(t)为t时刻中故障边的数目。由于可以看作是p(t)的估计值,f(t)可取为
注意到,对于任意的d∈{0,1,…,n-1},可以将沿第d维划分为k个子网络Hd,0,Hd,1,…,Hd,k-1。若边(u0u1…un-1,v0v1…vn-1)是d维边,则该边发生故障不会破坏Hd,0,Hd,1,…,Hd,k-1中任何一个子网络;若边(u0u1…un-1,v0v1…vn-1)不是d维边,则该边发生故障会破坏子网络Hd,ud。
在固定划分模式下,选定d*∈{0,1,…,n-1},将沿第d*维进行划分。在灵活划分模式下,若首条故障边为l维边,则将沿第l维进行划分。在任意时刻t,通过随机生成10 000次故障边集(每次生成的故障边集的边数为f(t))对这一时刻在不同划分模式下发生故障的子网络的平均个数分别进行仿真计算,并与例1和例2计算出的理论结果进行对比,具体结果如图3和图4所示。
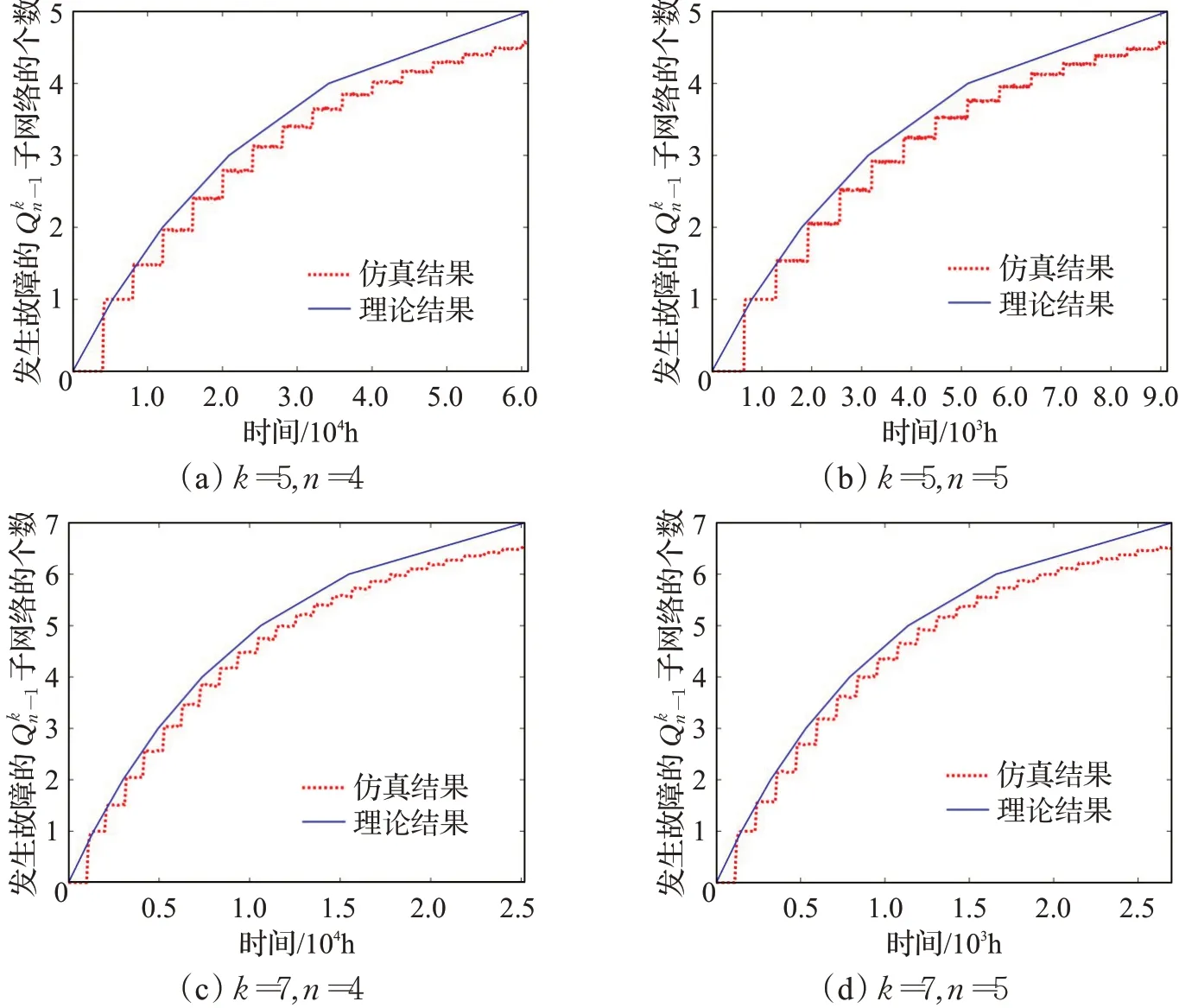
图3 固定划分模式下子网络可靠性分析结果Fig.3 Analysis results of subnetwork reliability in under fixed partition pattern

