基于多尺度等效模型的SiP热分析及散热优化
袁伟星,曾燕萍,张 琦,张春平
(中科芯集成电路有限公司,江苏无锡214072)
1 引言
微系统技术融合了微电子、微机电和微光电技术,通过系统架构和软件算法,将多个具有不同功能的有源元件与无源组件,以及MEMS、光学器件等集成于同一封装体,构成一体化软、硬件多功能集成,采用微纳制造及微集成工艺实现系统结构的微纳尺度化,朝着高密度、小型化、低功耗、高可靠性、高效率的方向演进[1-2]。微系统封装主要基于集成电路工艺方法的进步,发展趋势即系统级封装(SiP)技术,它主要通过中道及后道工艺实现,即通过对流片回来的芯片进行再布线(RDL)以及先进封装技术实现系统集成[3-4]。
高功率SiP采用晶圆级封装技术,包含大量微米级尺度的微凸点、硅通孔(TSV)等,是一种典型的多尺度复杂结构,且集成度的不断提高使SiP功率密度增大,导致封装中热管理问题愈发突出,开发快速准确的热仿真技术、实现有效增进SiP散热效能是封装设计中不可忽视的一部分[5]。卫三娟[6]采用串并联热阻思路,利用能量守恒法将微凸点与底填料等效为等效块,从而得出等效热导率。戈长丽[7]基于热阻网络的TSV单元等效,在等效单元面内热导率计算时采用并联导热通路,求得等效热导率。文献[8-9]采用等效热导率研究方法,合理简化模型同时显著降低计算资源消耗,大大提高了有限元仿真效率。
本文综合文献[6-7]的等效思路,将等效热阻网络运用于微凸点单元,在等效单元面内热导率上采用串并联思路,从而提取微凸点等效热导率,合理简化SiP热模型并进行误差分析,为后续SiP散热优化提供指导思路。
2 等效理论
针对微组件底部微凸点与底填料的多尺度情况,基于热阻网络的等效热导率计算,采用各向异性的均匀立方块代替大量微凸点和底填料,微凸点等效原理如图1所示。该等效热导率理论计算核心方法是:基于一维傅里叶导热定律和串并联电阻公式,得到单个周期单元等效热阻网络,再反推得到整个结构的等效热导率。

图1 微凸点等效原理
2.1 y方向等效热导率计算
对于y方向,在微凸点单元上表面施加一个均匀热流Qy(如图2所示),单元四周为绝热边界,则热流Qy全部沿着y方向传导,得到微凸点单元的并联热阻网络,热阻等效模型如图2(b)所示。

图2 y方向等效热导率计算模型
基于一维傅里叶导热定律和并联电阻公式,有:
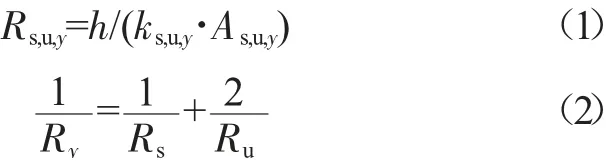
将部件投影面积用参数p、d、h代替,因此等效单元y方向的热导率ky为:

其中,Rs、Ru和Ry分别为微凸点热阻、底填料热阻和等效单元y方向热阻,ks、ku为微凸点、底填料材料热导率,As、Au和Ay为微凸点、底填料和等效单元在y方向的投影面积,d为微凸点直径,p、h为微凸点节距、高度。
2.2 x-z方向等效热导率计算
微凸点单元面内热导率相同,只需得到x方向的等效热导率。根据微凸点单元的对称性,取x方向单元的一半进行分析,微凸点单元侧视图如图3(a)所示。将模型分为A、B部分,其中A部分只含底填料,B部分含底填料和微凸点,得到整体的串并联热阻网络,等效热阻模型如图3(b)所示。
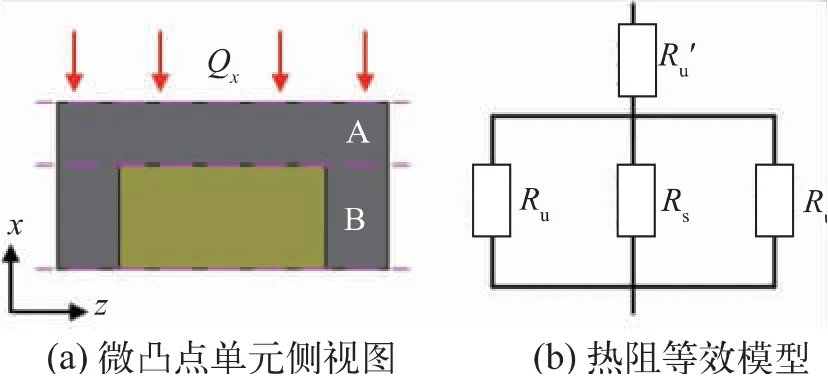
图3 x方向等效热导率计算模型
同理,有方程:
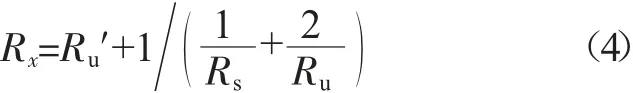
因此等效单元x-z方向的热导率kx为:

由式(3)、(5)可以得出,微凸点单元等效热导率的变化取决于微凸点单元组成材料热导率和微凸点节距与直径。
3 有限元模拟
采用三维建模软件ANSYS/SpaceClaim建立仿真模型,基于Workbench平台中Icepak软件进行热仿真,其中建模与热仿真流程如图4所示。
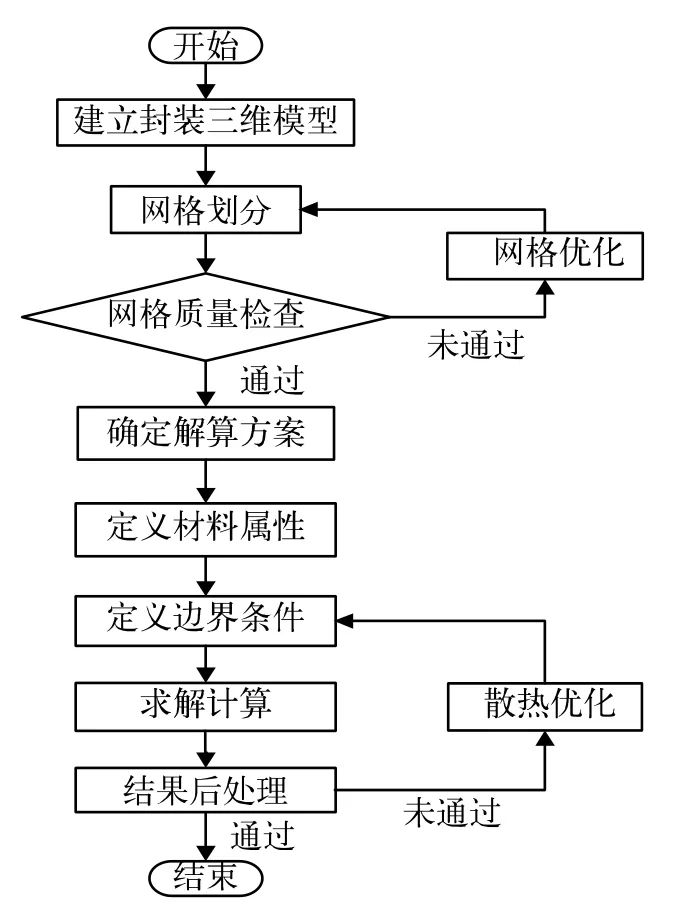
图4 建模与热仿真流程
3.1 热建模
高功率SiP采用陶瓷双腔封装,内部集成DDR微组件、DSP微组件、时钟驱动器和342颗阻容,主要器件尺寸参数如表1所示,其中DDR微组件为TSV互连的四层堆叠结构,DSP微组件为DSP裸芯片采用RDL互连,最终SiP封装形式为CCGA1489,尺寸为45 mm×45 mm×9.59 mm。因DDR微组件和DSP微组件内含有大量微米级尺度的微凸点,建立热模型时将微凸点与底填料简化成相同尺寸的等效块,基于微凸点等效后的SiP三维模型如图5所示。

图5 SiP三维模型

表1 封装主要器件尺寸、数量与功耗参数
3.2 布线层导入
将三维模型转化为Icepak可识别对象,根据仿真精度和研究目的要求,需在热模型内导入基板、RDL层的布线过孔信息。利用Siwave软件导出布线层文件,在Icepak内将EDA模型文件导入至相应位置,完成布线过孔导入的SiP模型如图6所示。

图6 SiP模型导入布线过孔
3.3 网格划分
网格质量好坏决定了求解计算精度及是否可以收敛,网格数量多少决定了计算资源与计算时间。因SiP模型复杂,网格划分采用层次化分析方法,主要思路为:先局部后整体,先进行微组件和单器件网格划分,再进行整体划分。在JEDEC机箱内采用非连续性、非结构化网格对仿真模型进行仿真划分,计算得到整体网格单元数为3173463,节点数为3527406,最小面对齐率为0.53,满足计算要求。
3.4 材料与方法
仿真中SiP总功耗为90.6 W,热源芯片功耗参数见表1,Bump等效块热导率和其他封装材料参数如表2所示。假设周围环境温度为25℃,仿真SiP在JEDEC机箱内自然对流下的温度分布,打开自然对流和辐射换热,设置重力参数为-9.8 m/s2。
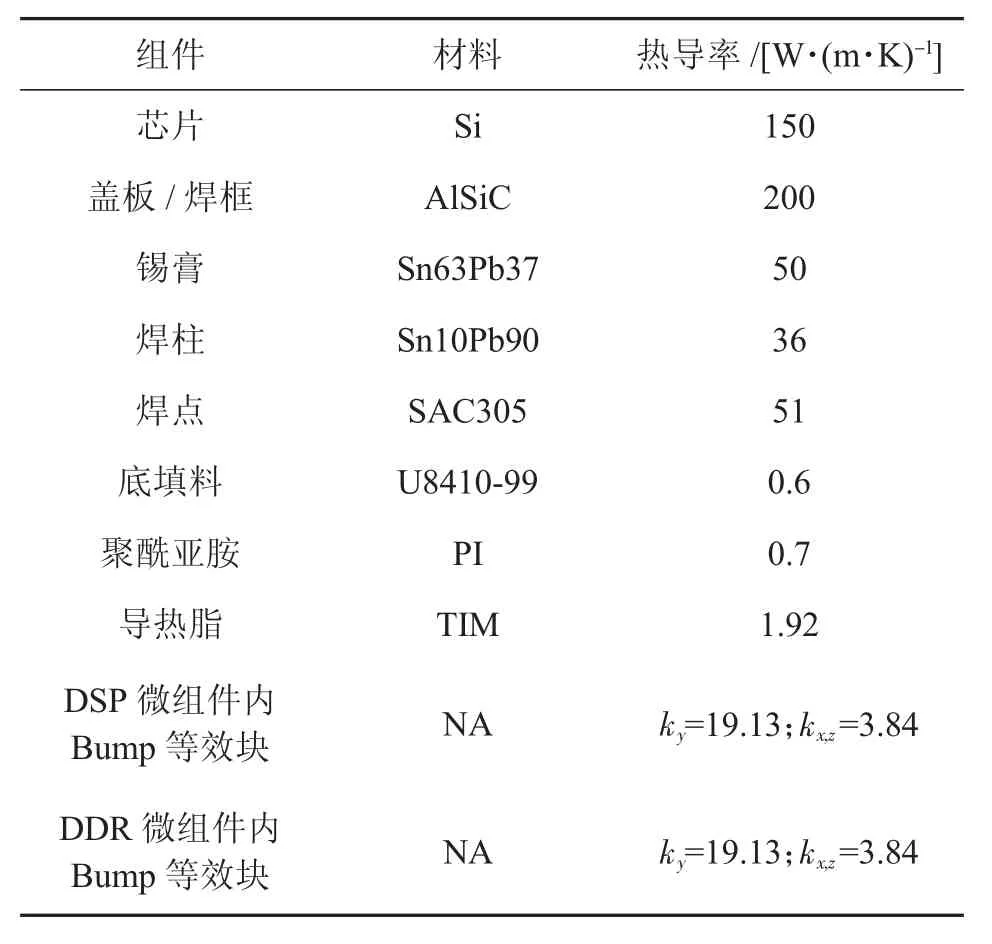
表2 CCGA封装的材料参数
3.5 热仿真结果与误差分析
图7 为常温下基于Bump等效SiP自然散热内部主要组件的温度云图,由整体可以看出上腔DSP微组件功耗较大且为主要热源区,但最高温度出现在下腔CLK芯片上,主要是CLK芯片热流密度达44.5 W/cm2,散热路径为上盖板通路,造成通路上的局部温度集中;焊柱和基板温度有所下降,远离基板中心位置的焊柱边界区域温度最低。图8为常温下精确SiP模型自然散热切面温度云图,表3为等效SiP与精确SiP仿真计算时间,已知误差λ和效率η计算公式为:
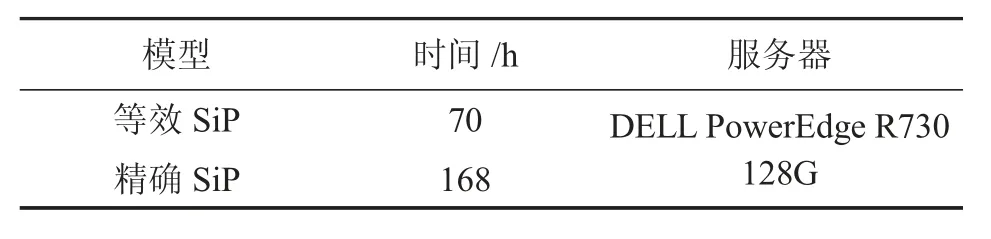
表3 等效模型与精确模型计算时间对比
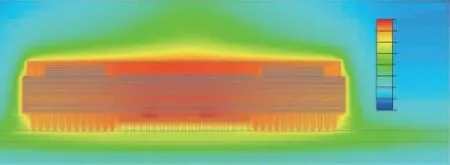
图8 精确SiP模型主要组件温度云图
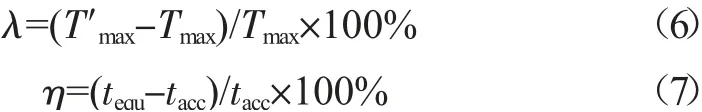
其中T′max、Tmax为等效SiP、精确SiP温度最高值,tequ、tacc为同温度下等效SiP、精确SiP仿真计算时间。由式(6)、(7)定量分析可知,基于Bump等效SiP最高温度值与精确模型最高温度值误差为7.6%,满足热仿真精度需求,同时使计算时间节约了58 %,大大提高了仿真效率。文献[7]中求解TSV精确模型与等效模型时,计算总效率提高了66.7 %,但其精确模型较为简单,本文SiP建模及求解复杂程度较高,为复杂SiP热仿真提供更为全面的数据支撑。硅芯片失效温度为175℃,考虑到仿真误差,将芯片结温控制在160℃以内,图7结果显示SiP整体发热过高,因此需对SiP系统进行辅助散热设计,将温度控制在允许范围内。
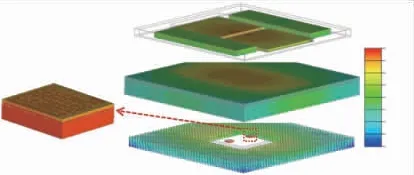
图7 基于Bump等效SiP主要组件温度云图
4 散热优化设计
按以下3种方案对基于Bump的高功率SiP进行辅助散热优化:
①在SiP上盖板添加叉翅散热器(85.4 mm×85.4 mm×30.4 mm),主要是让SiP产生的热量通过散热器快速传导并释放出去;
②在方案①的基础上进行强迫风冷,假设风速为3 m/s,通过流体与SiP器件进行热量交换,从而对SiP进行散热;
③在SiP上盖板设计单相微通道热管结构(50 mm×50 mm×4 mm),单通道截面尺寸为0.5 mm×3 mm,微通道内液冷水为环境温度,流速为0.2 m/s。
图9 (a)、(b)、(c)分别为SiP在方案①、②、③下的切面温度云图分布,可知方案①能使SiP最高温度降低41.7%左右,方案②的散热能力远超于方案①,方案③散热能力略优于方案②,主要原因是:(1)液冷表面传热系数高于强迫风冷,自然对流表面传热系数小于强迫风冷;(2)SiP下腔芯片主要散热通道为上盖板,易于下腔形成局部温度集中。不同散热方案下基于Bump等效SiP最高温度如图10所示,SiP内最高温度值随着表面传热系数的增大而减小,方案②、③能使SiP最高温度保持在160℃以内,此时SiP无温度失效风险。
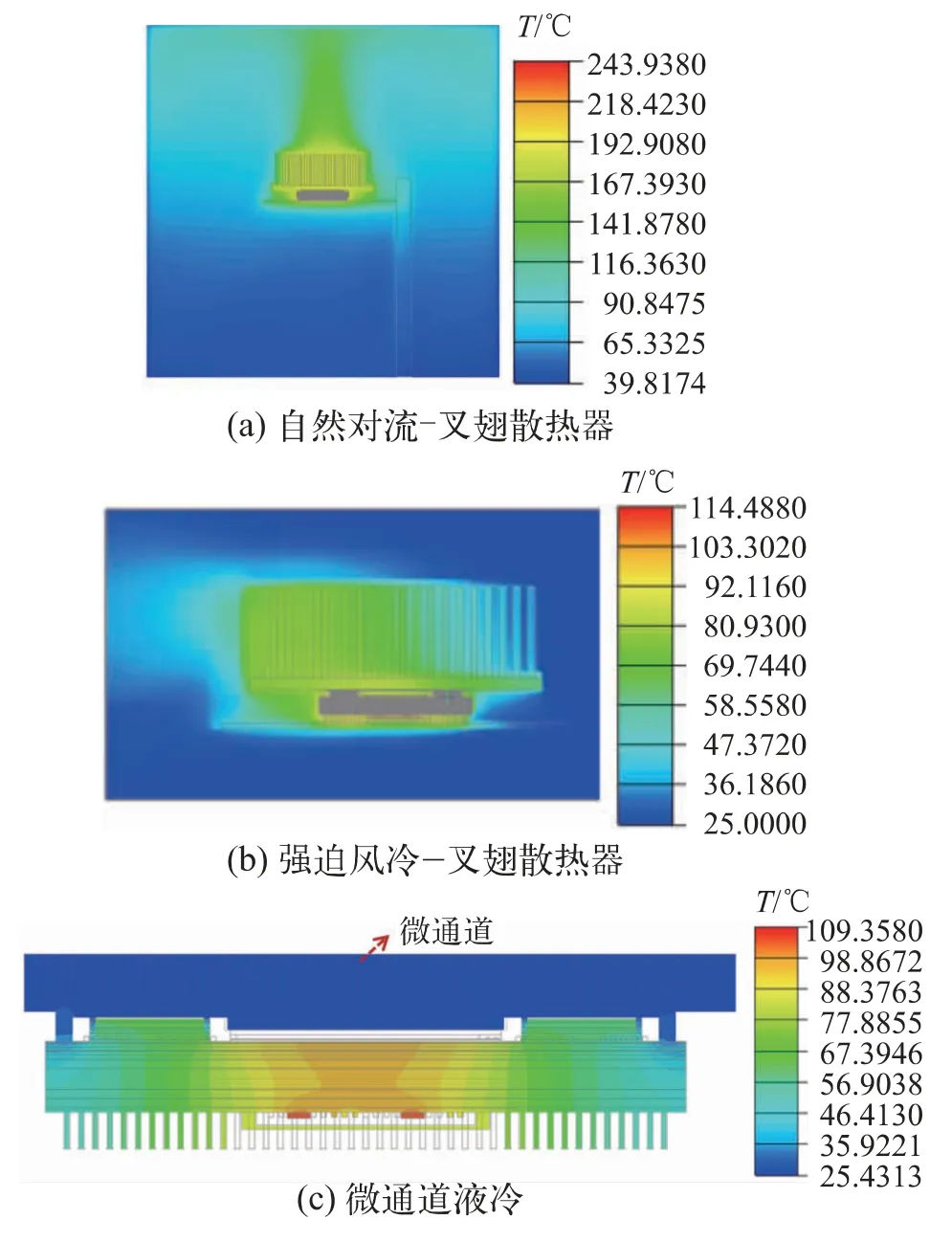
图9 不同散热方案下基于Bump等效SiP切面温度云图
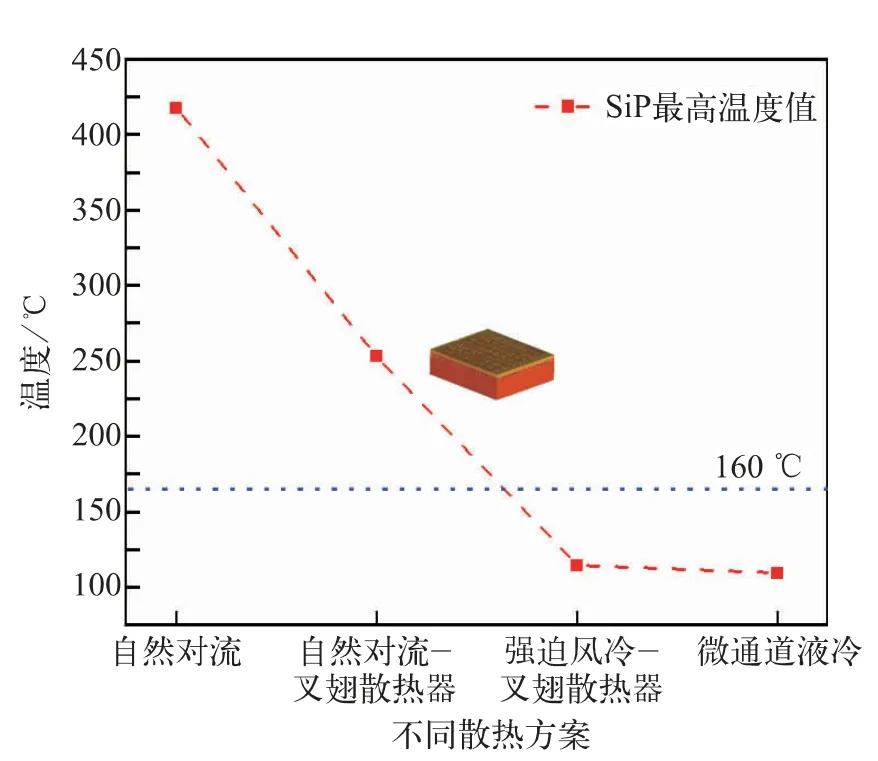
图10 不同散热方案下基于Bump等效SiP最高温度
5 结论
本文基于等效理论方法,将多尺度SiP封装结构简化成含等效热导率块的三维结构热模型,该方法有效简化SiP内存在的大量微凸点,快速获得封装结构温度场分布结果,与精确封装结构热仿真相比效率提高了58%,同时仿真误差为7.6%,保证了仿真精确度。在等效SiP热模型进行RDL、基板层导入布线过孔信息,是提高仿真精度的手段。对比SiP 3种散热优化设计方案,可知微通道液冷热沉散热效果最佳,后续可设计不同微通道结构,解决大功耗SiP散热需求。本文的分析方法对今后多尺度大功耗SiP热仿真及散热优化具有一定的指导意义。

