多智能体系统任务分配实验设计与实现

张 佳， 任亲浩

（北京理工大学，自动化学院，北京100081）

0 引 言

多智能体系统（Multi-Agent Systems，MAS）是指一群具有局部范围信息感知、处理和通信能力的自主移动智能体，通过系统间高效的协同合作能力，实现单个智能体所不能完成的各种艰巨、复杂的任务［1-2］。多智能体系统分布式协同控制是人工智能研究的热点，也是智能机器人的一个重要研究方向，其相关的教育是培养信息技术、智能技术及工程技术类人才的有效手段，已成为国际教育界关注的热点［3-4］。对自动化领域人才培养，增强学生综合实践能力和处理复杂工程问题的能力，培养拔尖、创新人才具有重要意义，是提高人才培养质量重要的一环［5-6］，其实验、实践教学在学生自主工程能力的培养中占有重要位置［7］。为让学生能掌握多智能体系统相关方面的最新研究动向，多智能体的协同控制在高校教学中已逐步渗透至研究生和本科生，出现在控制专业的课堂上，但配套的相关实验屈指可数。

结合多智能体系统在实际问题中的应用，构建分布式多机器人系统仿真平台，设计并实现分布式多智能体系统协同探测［8］任务分配的仿真，便于学生将理论与应用相互结合、融会贯通，培养学生的实践能力。配合以问题为导向（Problem-Based Learning method，PBL）教学方式，该仿真平台可以开展机器人、多智能体系统相关课程的配套实验，促使学生从以往的被动式学习向以探究科学知识、解决复杂工程问题为目标的主动式学习快速转变［9］。

1 多智能体探测任务分配实验设计

1.1 仿真环境构建

本实验环境构建采用AnyLogic［10］8.5.2专业版。用栅格化地图构建多机器人探测任务的仿真环境，并对相应栅格的高度作出设置。假设每5单位距离为1 m，设置栅格大小50×50×10，即一个栅格的体积为200 m3。现建立一个12×14×16的三维环境，即纵向共12个栅格，横向共14个栅格，环境高度为6个栅格。实验环境的平面效果、立体效果如图1、2所示。实验中共设计了4种高度，其中，白色方块为边界，绿色方块为平地，黄色方块高度为10，粉色方块高度为20，红色方块高度为30，红色圆点表示任务点。

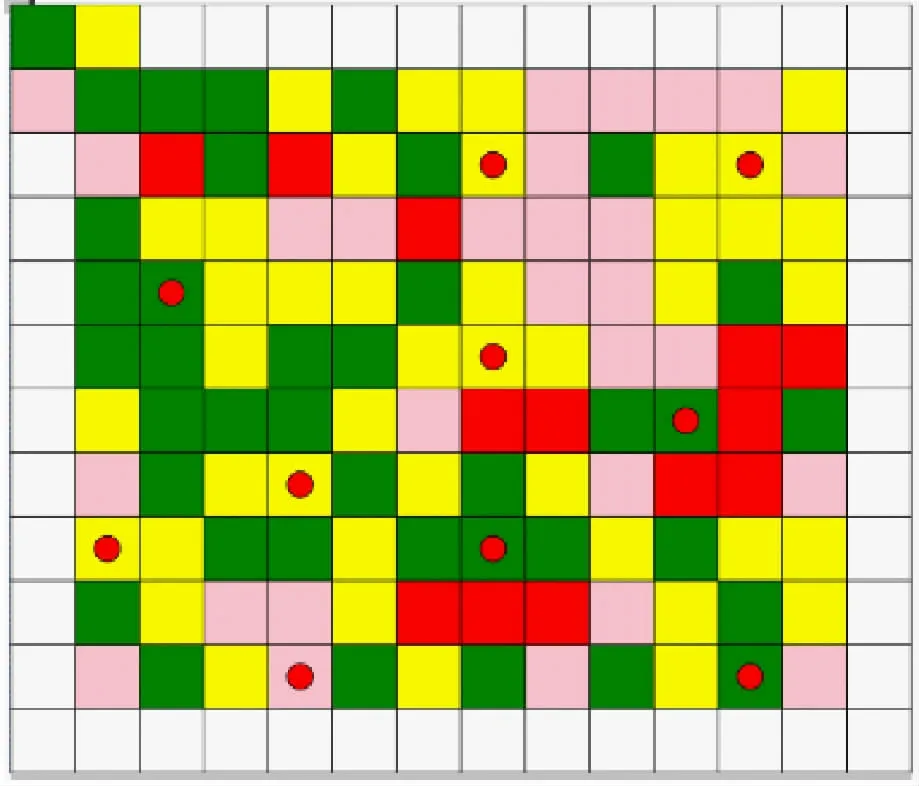
图1 平面地图效果

图2 立体地图效果

1.2 协同探测任务分配实验建模

基于机器人自身能力的限制，仅凭单个机器人难以完成对多个地区探测的任务，需要多个机器人进行协同探测。以分布式异构多智能体系统执行探测任务为背景，实验内容是采用某种优化分配方法，为实现多个机器人协同探测任务开展任务分配工作，使系统中的多个机器人能够协同工作，达到总体工作最优。

实验环境中的已知信息包括任务点的位置、任务对探测能力的需求、多机器人系统的出发点、能力等，并且都不会发生变化。需要解决的问题描述为：给定N个能力异构的机器人和M个需求能力异构的任务点，如何进行探测任务的分配，能够得到一个高效无冲突的分配方案，使得所有机器人执行任务的总航迹时间最短。

式中：Bi=｛B1，B2，…，Bj｝i=1，2，…，N为机器人i执行任务的集合；T=｛T1，T2，…，TM｝为所有探测任务的集合。实验中，每个任务都是单机器人任务，即每个任务只会分配给一个机器人；所有机器人都是单任务机器人，它们可以拥有多个任务，但只能执行完一个任务后才能执行其他任务。

在多机器人系统进行任务分配的过程中，需要遵循以下规则：

（1）所有机器人执行任务时优先执行距离当前自身位置最近的任务；

（2）机器人能力足够时才能获得对应的任务，即自身能力满足对应任务的需求。

用Li表示机器人i完成自己所有任务的总时间，xij为分配函数，机器人i∈U，U=｛1，2，…，NU｝，任务j∈G，G=｛1，2，…，MG｝。所有机器人执行任务的时间要求最短，即

任务j分配给机器人i时分配函数xij的值为1，否则为0，即

每个任务只分配给1辆机器人，即

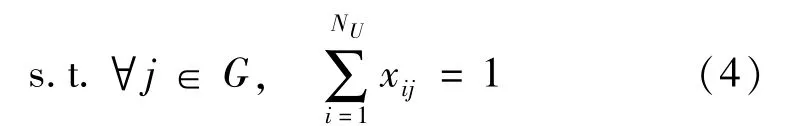
所有的任务都会被执行，

多机器人任务分配的目标函数值z，由所有机器人执行任务时间的集合中的最大值决定。即在同时满足任务分配无冲突以及所有任务都有机器人完成这2个约束条件的前提下，尽量使得z的取值最小，z越小表示所有机器人完成任务的时间越短。

1.3 探测任务分配方法

实验采用改进的合同网拍卖算法［11-12］进行任务分配。实验分为2个阶段，第1阶段为机器人选择任务以及报价，每个机器人根据自身能力的强弱选择能够执行的任务，然后更新自身的信息，计算其选择了的任务的出价；第2阶段为冲突消解［13］，各机器人之间对于选择的相同任务进行出价比较，出价最高者得到该任务，竞标失败的机器人从自身移除该任务。

多机器人任务分配的步骤如下：

步骤1初始化参数。包括各机器人的能力系数集合、出发点等信息，以及任务的所需能力系数集合、位置等信息；

步骤2构建任务集。对于每个机器人而言，若任务满足条件CT≤CR，那么该机器人将此任务加入自身的任务集之中；

步骤3构建路径集和时间集。根据就近原则重新排列任务集得到路径集，基于路径集的执行任务顺序信息计算出时间集；

步骤4计算出价。根据出价公式得到每个机器人对于路径集中各任务的出价，更新自身的胜者集和价格集；

步骤5冲突消解。根据贪心算法［14］解决旅行商问题［15］，对于所有任务进行顺序排列，随后按照此顺序依次进行冲突消解。每个机器人之间互相通信协商，进行出价对比，价格最高者保留任务，其余价低者删除任务集中的该任务。所有机器人之间协商结束后，重新进行步骤3直至所有任务完成冲突消解，算法结束，得到最终任务分配结果。

该步骤的流程图如图3所示。

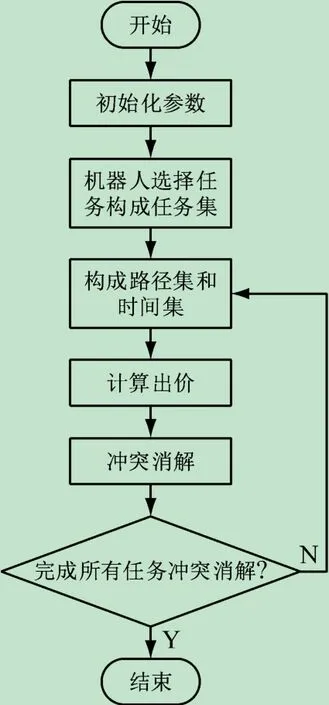
图3 探测任务分配流程图

1.3.1 信息结构

在多智能体系统的任务分配过程中，每个机器人的地位都是平等的，它们之间都可进行通信。定义机器人的集合为U=｛1，2，…，N｝，任务点的集合为T=｛1，2，…，M｝，即表示系统中有N个机器人以及M个任务。每个任务根据所需求的能力不同，定义任务j所需能力系数集合为CTj=｛C1，C2，…，Ck｝，Ck为任务对于探测能力的需求能力系数，Ck越大表示该任务点对于探测能力的需求越高。通过不同的需求能力系数组合，就能表示能力需求异构的任务。对于每个机器人，都包含以下几个信息：

（1）能力系数集合CR。定义CRi=｛C1，C2，…，Cn｝为机器人i的能力系数集合，对应探测能力的强弱。根据机器人系统任务分配规则，只有当机器人的能力系数集合中每一项元素都大于对应任务的所需能力系数集合的对应元素时，该机器人才能对此任务进行选择并加入自己的任务集合里面。当Cn=0时，表示该机器人不具备该种探测能力，Cn越大表示机器人该种能力越强。

（2）任务集Bi。定义Bi=｛B1，B2，…，Bj｝，Bj为任务j，该集合表示机器人i的可执行任务集合，即该机器人通过对能力系数进行比较，将所需能力系数不超过自身能力系数的任务都加入自身的任务集中。

（3）路径集Pi。定义Pi=｛P1，P2，…，Pj｝，Pj为第j个执行任务，Pj=｛1，2，…，M｝为任务的编号，该集合表示机器人i执行任务的顺序。

（4）时间集ti。定义ti=｛t1，t2，…，tj｝，该集合为机器人i按照路径集的顺序从起始点到达任务j的时间。由于具体环境的不确定性，该集合是根据机器人到任务点的空间直线距离以及机器人的行驶速度进行计算的。由于该集合是基于路径集计算的，每一个路径集元素对应一个时间，所以该集合元素的数量与路径集相等。当考虑时间时，该集合作为机器人出价的重要参考因素。

（5）胜者集Wi。定义Wi=｛U1，U2，…，Ui｝，Ui=｛1，2，…，N｝。该集合共有M个元素，对应M个任务，表示机器人i认为的目前系统的分配结果，第n个元素Ui为第n个任务分配给机器人i执行，其中0＜n＜M+1。

（6）价格集Yi。定义Yi=｛Y1，Y2，…，Yj｝，该集合为目前每个任务对应的最高价格，如果在机器人的认知里，某个任务目前还没有分配给任何机器人，那么对应元素为0。它和胜者集是对应的，胜者集表示任务分配给哪个机器人，价格集为对应机器人的出价。

1.3.2 选择任务

每个机器人根据自身的能力系数集合，选择可以执行的任务，并且将这些任务加入自己的任务集当中。通过贪心算法对任务集进行重新排列得到路径集，根据路径集的顺序和速度等相关参数计算出自身的时间集。对路径集中的任务进行报价

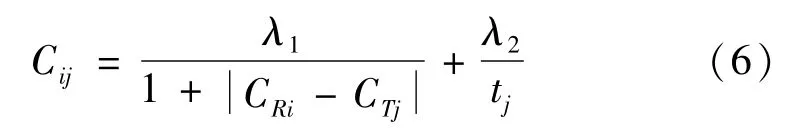
式中：Cij为机器人i对于任务j的出价；CRi、CTj分别为机器人i的能力系数集合以及任务j的所需能力系数集合，|CRi-CTj|=（CR1-CT1）2+（CR2-CT2）2+…+（CRk-CTk）2为机器人与任务的匹配程度，该值越小表示两者匹配程度越高，最佳匹配表现为该结果为0；tj为机器人按照当前路径集到达任务j的时间，即时间集中对应的元素；λ1、λ2分别为机器人和任务匹配程度的影响权重系数以及时间的影响权重系数，它们的大小视具体情况而定。

每个机器人计算出价后，都会更新自身的胜者集和价格集。在初始化参数阶段，对于自己选择的任务，先认定自己为胜者，价格集对应元素也为自己的出价，对于未选择的任务，胜者集和价格集都认先设定为0，即目前没有分配任务给机器人。

1.3.3 冲突消解

在所有机器人都完成任务选择后，机器人之间开始通信协商以达到解决冲突的目的，得到最后的任务分配结果。由于在“选择任务”阶段中，每个机器人得到的路径集以及时间集等集合都是基于距离最近原则构造的，在冲突消解阶段同样基于距离最近原则。依照贪心算法解决旅行商问题，将任务集中的所有任务都分别看作一个城市，假设一辆试验车为商人，那么可以得到该试验车遍历所有任务的执行顺序。通过该方法从起点开始，所有的任务都根据每次选择距离当前点最近的任务点排列起来了，以此构成一个所有任务的路径集合。根据该集合中的顺序依次进行冲突消解，确保每个机器人的路径集不会出现混乱，即每1次冲突消解时，机器人对于进行冲突消解的任务的出价都是当前阶段该机器人能够给出的最高价格，同理这也确保了每次任务都分配给了最高出价的机器人。每进行完机器人对于一个任务的出价比较后，价格最高的机器人得到任务，其余机器人从路径集中删除该任务。

每次完成一个任务的冲突消解后，所有机器人都会重新构造自己的路径集、时间集等，根据新的时间集计算出价，再进行下一个任务的冲突消解。直到所有任务都完成了冲突消解，算法结束，得到最后的分配结果。

2 实验数据及结果分析

2.1 任务点及机器人相关参数设置

给定5个异构能力的机器人以及10个所需能力不同的任务点，设定每个机器人的行驶速度为1 m/s，翻越能力为2 m。即在实验中每次只能同高度移动或者移动到高度差为2 m的位置。根据能力异构，设置3种探测能力，即侦察、抗干扰和数字测绘，它们的上限都设定为4。各机器人参数和任务点参数见表1、2。

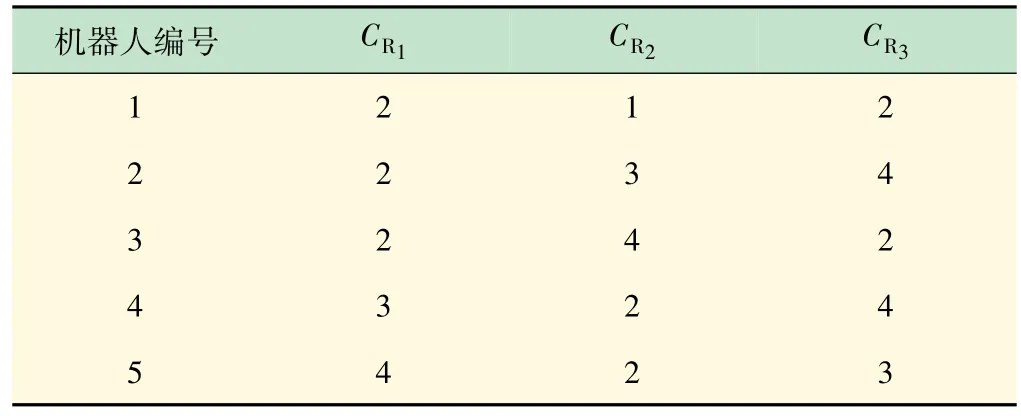
表1 各机器人的参数

各机器人其余参数如起点、速度和翻越能力等均相同，实验仅考虑能力异构。表中CR1～CR3对应3种探测能力，各参数的大小表示对应能力的强弱。

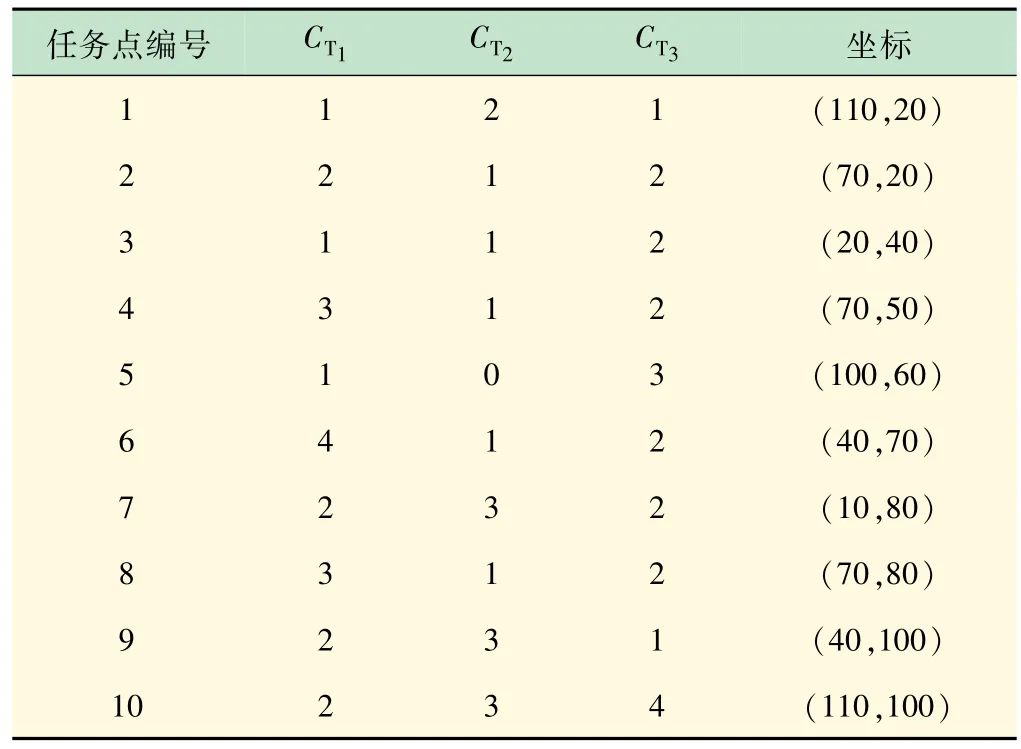
表2 各任务点的参数 mm

2.2 实验结果

考虑到任务匹配程度和时间对于机器人出价的影响，实验中设置了不同的λ1和λ2，得出了如表3所示的分配结果。

表3 各机器人的路径集

在权重系数各为0.5时，各机器人的时间集见表4。

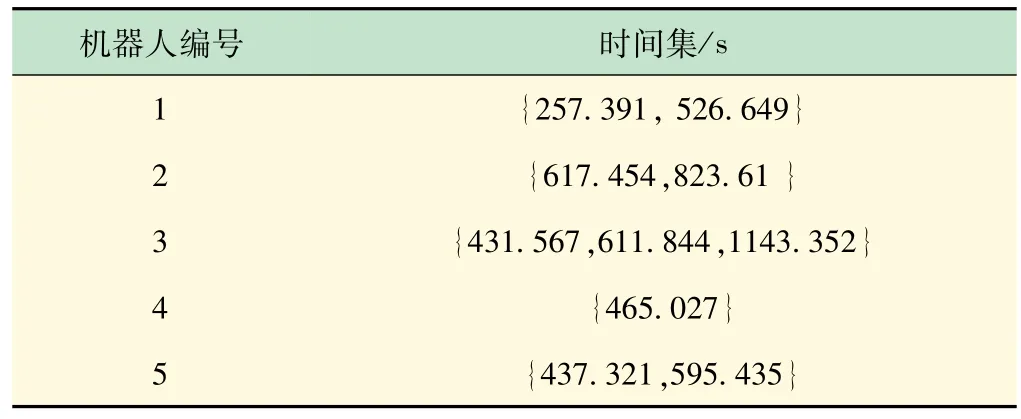
表4 各机器人的时间集

由表4可知，地图的执行任务时间为1 143.352 s。根据实验结果可知，每个机器人路径集中的任务都是符合自身能力的，并不存在某个任务同时出现在多个机器人的路径集中。说明本实验所采用分配方法的结果是合理、无冲突的。

由实验结果可见，任务分配结果主要受匹配程度和时间集影响，当前者的权重系数大于后者时，任务的分配结果倾向于每个机器人执行与自己匹配程度高的任务，同时减小任务点之间距离对于分配结果的影响；当后者的权重系数大于前者时，任务的分配结果倾向于执行任务时间短，同时减小机器人与任务的匹配程度对于分配结果的影响。

3 结 语

本文设计并实现了多智能体系统协同探测任务分配实验，其中任务分配算法既可以使用改进合同网拍卖算法，也可以让学生自行选择。实验具有较强的可扩展性，探测任务分配完成后，后续还可进行机器人在执行探测任务时的路径规划实验，根据不同的任务需求，不断扩充实验内容。该实验可作为机器人、多智能体系统等理论课程的配套实验，辅助理论教学，提高学生的理解能力、解决问题能力及创新能力。