一种改进型RatSLAM算法构建认知地图的研究

洪涛，史涛,2，任红格,3

（1.华北理工大学电气工程学院，唐山063210；2.天津理工大学电子工程学院，天津300384；3.天津城建大学控制与机械工程学院，天津300384）

0 引言

随着社会的智能化发展，将会存在越来越多的机器人与我们生活在一起，它们将面对这个复杂且多变的社会环境，这就要求机器人在未知环境中工作时需要更精确的定位与识别，以此来对机器人进行即时定位与地图构建（Simultaneous Localization And Mapping，SLAM）[1]，目前较受欢迎的有基于生物海马神经元机制的RatSLAM算法，Milford教授通过对大鼠大脑假设的“位姿细胞”进行数学建模，通过视觉里程计驱动导航系统，建立一个具有仿生性的实时定位与地图构建算法，该算法具有更完善的生物合理性以及强的环境适应性[2-3]。实验表明这种纯视觉的仿生SLAM算法在室内静态环境中有着良好的定位导航能力[4]，但在SLAM系统的前端中对于视觉里程计过于依赖，存在着图像匹配精度受限，累计误差以及环境适应性较差等问题，因此RatSLAM还需要更进一步的优化[5-8]。Tubman等人曾提出引入RGB-D深度信息到RatSLAM算法中来提高精度，但在具体实践中具有较大难度，实用性还有待提升[9]，张潇等人也尝试建立融合光学双轴速度传感器和MIMU信息的航迹推算模型，但系统的鲁棒性受到影响[10]。孙新柱等人也提出过结合SURF算子的RatSLAM的方法，但实时性并无具体的提升[11]。也有为解决RatSLAM算法视觉模板匹配较差以及特征点误匹配的问题而提出的将特征点与RatSLAM相结合的算法，提取RGB图像的特征，令FAST关键点与BRIEF描述子像匹配，但在动态环境中的跟踪效果不太理想[12-13]。

本文在传统基于海马神经元的RatSLAM算法基础上，对O-FAST（Oriented FAST）关键点进行提取，再使用渐进一致采样（PROSAC）算法进行特征点匹配，实现图像帧间匹配并重新定位，提高特征匹配的准确性以及系统鲁棒性，最后再通过仿真环境进行轨迹对比来验证构建的地图的准确性。

1 RatSLAM算法实现

RatSLAM系统主要包含:位姿细胞（Pose Cell）、局部场景细胞（Local View Cell）、经历地图（Experience Map）。每个位姿细胞代表着机器人某个时刻的位置与方向信息，每个局部场景细胞表示着机器人某时刻所经历场景的图像特征信息，而经历地图是将两者相结合，将多个时刻的位姿与场景信息整合成相关地图[14]。RatSLAM算法流程图如图1所示。

图1 RatSLAM算法流程图

1.1 位姿动态表达

1.1.1 兴奋性更新（Excitatory update）

构建一个三维的高斯矩阵ε来表示兴奋度的权重，εabc的三维矩阵是由一个二维的高斯矩阵来表示位姿细胞的兴奋性和一个θ维的矩阵来表征细胞兴奋一维分布的乘积，其计算公式为：

式中，vxy和vθ分别为平面（x,y）和表示方向θ维的方差常量，a,b,c是x,y,θ的分布系数。计算公式如下：

式中，Dx,Dy,Dθ是位姿细胞在（x,y,θ）的三维矩阵元素，在位姿检测时，对相应位姿细胞进行刺激，因刺激而产生的兴奋度变化活性ΔE为：

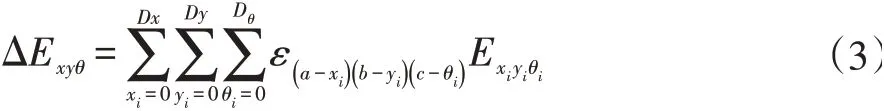
1.1.2 抑制（Inhibition）

位姿细胞相互间会产生抑制，在兴奋度更新期间，每一次的位姿估计都会导致抑制权值矩阵ξ增加，此时需要引入一个全局抑制输入μ对位姿细胞活性进行抑制，抑制可以看作是一个迭代的过程，抑制后的细胞活性为：

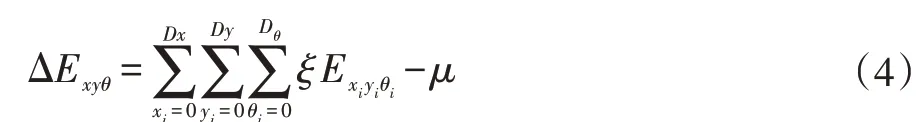
1.1.3 标准化（Normalization）

CAN神经网络上的位姿细胞总活性需要保持不变，通过标准化可实现总活性保持为一。标准化公式如下：

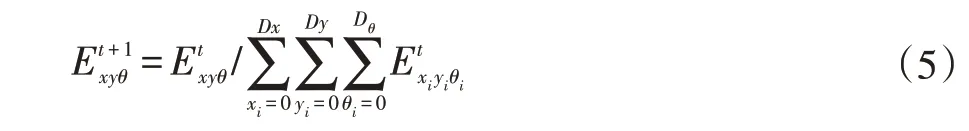
1.2 路径积分

路径积分表示转换角速度与线速度的信息进行迭代更新，在RatSLAM算法中即表示由里程计与（x,y,θ）三维坐标获取的信息通过转码来更新当前的细胞活性。更新后的细胞活性为，计算公式为：

式中，a表示残余数矩阵，它与位姿细胞单元相乘表 示 被 注 入 活 性 的 总 量，δx,δy,δθ表 示 三 维 空 间（x,y,θ）上的整数偏差，由以下公式计算得到：

这里λx、λy和λθ是路径积分常数。v为平移速度，ω是传感器获得的角速度，θ为细胞优先朝向。

1.3 经历地图

在经历地图中，我们通过构建一个独立的三维坐标系（x,y,θ）来表征每个ei的空间位置，记Li为经历ei在地图中的位置，ei的向量描述为：

获得了经历ei的向量描述，便可以通过对比场景的信息来完善地图的构建。判断当前经历ei对应的位姿细胞状态Pi与局部场景细胞Vi跟之前所存储的经历ei是否匹配，若是不匹配，则求出插值S，公式如下：

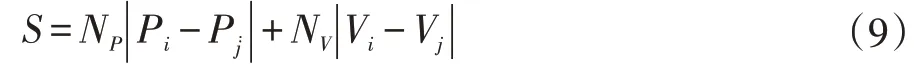
式中，NP为当前时刻与上一时刻的位姿细胞之间的权值，NV是当前时刻与上一时刻局部感知细胞之间的权值匹配。通过插值S与阈值相比来判断目前的场景是否需要更新，若S大于阈值，则判断当前场景为新场景，记为一个新的ei经历。

2 对RatSLAM算法的改进

基于RatSLAM仿生算法去构建认知地图，本文提出了一种结合ORB特征点的RatSLAM算法，通过在ORB特征点的提取中引入自适应阈值来进行关键点提取，在匹配阶段利用渐进一致采样算法对特征点进行图像匹配，通过减少迭代的次数来加强算法在动态环境中的实时性与精确性。

2.1 改进特征点匹配

为了解决特征点匹配可能会出现误匹配、低精度的问题，本文结合渐进一致采样算法（PROSAC）来进行特征匹配，可以减小匹配对的计算量，优化系统的动态实时性。

渐进一致采样算法是先对数据点进行排序，在评价函数值最高的数据点子集中随机采样，即从不断增大的最佳对应点集合中进行采样，这样整体的采集样本中正确的点集就会比错误的点集要多，因此可以节省计算量，提高匹配速度。

在提取的特征点的匹配对中选取离特征点与最近和第二近相邻点的汉明距离（Hamming Distance）之比为：

Vp是特征点p的特征向量，Vap是离特征点p最近的特征向量，Vmp是离特征点p第二近的特征向量，分别求得特征向量与最近点以及特征向量与次近点的距离D，得到汉明距离之比R。

汉明距离之比R将决定数据点子集中采样点匹配质量的好坏，若R小于动态阈值v，则匹配按照由好到差来排列，此时得到质量函数如下式：

渐进一致采样算法特征匹配的实验步骤：

（1）设定迭代最大次数为X。

（2）检测当前迭代次数，若迭代次数大于迭代最大值，则返回统计的内点数量最大的一组数据；若迭代次数小于最大迭代次数，流程进入下一步。

（3）将数据点子集中的采样点以匹配质量从好到坏排序得到数据点集合U，从中选取N个较好的数据子集。

（4）再从N个数据子集中随机选取n个匹配点数据来计算模型的参数β。

（5）判断模型的参数是否大于设定的误差阈值ηprosac，若参数小于阈值，则判定该点为内点，若大于阈值，则舍弃匹配点。

（6）设定数量阈值ηnumber，判断内点数量若大于阈值，进行特征点误匹配的剔除，得到数学模型；若内点数小于阈值，则返回步骤（2），当前迭代次数加1。

PROSAC算法特征匹配的流程图如图2所示。

图2 PROSAC算法的特征匹配

2.2 闭环检测

在实际的仿真中所使用的视觉里程计以及传感器是会产生累计误差的，这些误差将会对认知地图的构建产生影响，因此为验证改进之后的匹配精度效果，我们需要对构建的地图进行闭环检测，闭环检测就是物体运动的实际目标点与预测的位置点进行对比，闭环检测的示意如图3所示，该示意图就显示出了当累计误差的不断积累会使物体运动出现偏离目标点的现象。因此，本文进行机器人仿真实验的闭环检测来减小误差，提高认知地图构建的鲁棒性。

图3 闭环检测

本文使用ROS平台进行机器人运动仿真，将采集的视觉图像进行闭环检测，方法如下：

（1）使用采集的图像进行灰度处理，再将图像信息转换成矩阵。

（2）对每一幅图像与之前所保存的图像进行视觉模板匹配的检测，这里设定相似度的阈值为0.75，判断图像是否达到阈值。

（3）当图像匹配度大于等于阈值，判定与该图像为储存过的图像，与之相对应的神经元细胞也是达到了阈值。

（4）判定两个图像场景的采样间隔是否大于50，此步骤是为避免出现机器人原地运动的现象，若采样间隔大于50且相似匹配度超过阈值，则判定检测到闭环点位置；若不满足二者之中的任一条件，则判定闭环检测未完成。

3 实验分析

本文实验采用的是Ubuntu操作系统下的开源平台ROS—机器人操作系统进行仿真，实验数据来自于德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合构建的KITTI开源数据集，通过自动驾驶汽车以及传感器对行车环境进行数据采集，数据采集平台装配有2架灰度摄像机，2架彩色摄像机，1个Velodyne64线3D激光雷达，4个光学镜头，1个GPS导航系统。

3.1 特征点匹配对比实验

对提取的特征点利用PROSAC算法进行匹配。参数设定，图像匹配特征点的汉明距离D为最小距离的两倍，汉明距离之比R设阈值为0.6，特征点设置为300。

实验结果如图4所示，为使显示较为清晰，匹配的连线通过不同颜色连接。可以看到，图4（a）显示的传统算法在图像匹配时存在匹配对较多，误匹配概率较大等问题；图4（b）为改进算法匹配图；图4（c）显示的是SURF+RatSLAM算法的匹配效果，匹配率相较于传统RatSLAM具有一定优势，但在匹配时间上耗时较久；图4（d）为本文算法匹配效果图。通过对比可以看出相比较于传统算法与SURF+RatSALM算法，改进之后的算法通过约束筛选，能够降低误匹配对，只对图像关键点像素进行匹配，并且减少了重叠冗杂的现象，缩短图像匹配的时间，提升算法的动态性能。

图4 RatSLAM算法改进前后匹配效果的对比

对实验的匹配率进行分析，结果如表1所示，本文所提出的改进型RatSLAM算法相比较于传统算法以及另一种结合SURF算子的算法在匹配成功率上有所提升，改进后的RatSLAM算法通过筛选特征点得到了更精简的匹配对，在匹配的速度与匹配精度上优于传统的RatSLAM以及结合SURF描述子的RatSLAM算法。

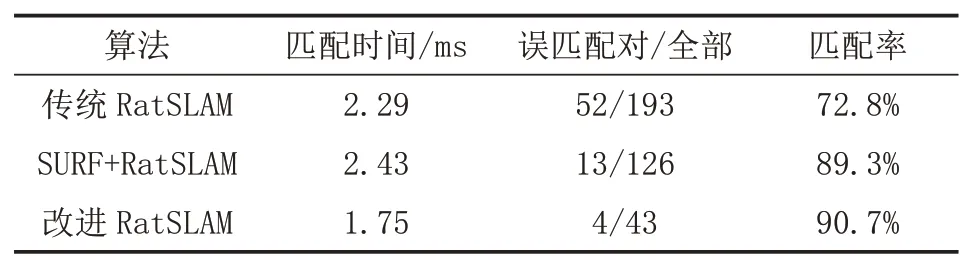
表1 RatSLAM算法改进前后特征提取与匹配的时间对比

3.2 闭环点检测实验

本文通过在ROS中搭建仿真环境进行闭环检测验证构建地图的精确性，仿真环境地图如图5所示。实验分成两个对照组，一组仅凭借里程计自带算法自主导航构建地图，另一组基于改进后RatSLAM算法的经历地图，机器人图像采集0.2s/帧，设定运行速度最大不超过0.1m/s，角速度0.05rad/s，图6（a）是由里程计获取信息得到的地图，图6（b）是本文改进后RatSLAM构建的经历地图，可以看出传统的里程计构建的环境地图会因为累计误差而产生漂移，而本文所构建的地图在闭环检测中的精度更高。

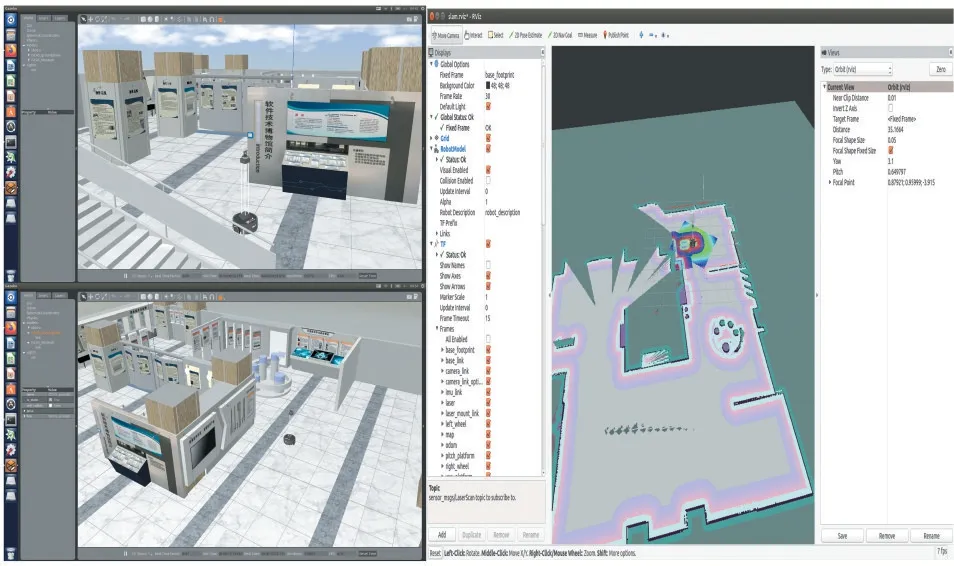
图5 仿真环境

图6 RatSLAM算法改进前后的闭环检测对比

通过图像匹配与闭环检测得到的误差数据如图7所示，改进后的算法在地图的定位精度上有着明显的提升。本文采用均方根误差（Root Mean Square Error，RMSE）公式进行偏差分析，偏差的大小反映算法在实时匹配中准确性。式中N表示采样的次数，ui表示第i采样对应的图像观测的位置坐标，Ui0表示第i次采样时的真实位置坐标，通过计算来验证改进前后Rat⁃SLAM算法在定位匹配上的准确性与稳定性。从表2的结果可知，传统算法的均方根误差值要大于改进后的算法，说明本文算法的仿真结果与真实轨迹的离散程度更小，更贴近真实轨迹，也说明本文算法在图像模板匹配定位上有更高的精确性和鲁棒性。

图7 累计误差对比图

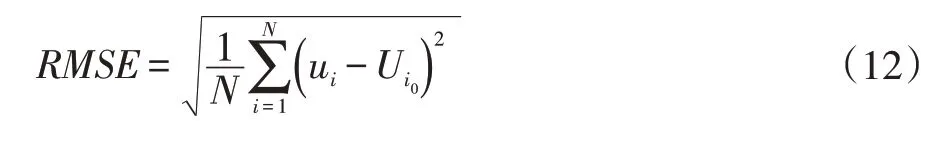
表2 RatSLAM算法改进前后均方根误差对比

4 结语

本文通过引入ORB特征点对传统RatSLAM算法的图像提取与匹配进行改进，设置一种自适应阈值对图像的特征点提取进行筛选，简化特征点的冗杂与聚集，实现匹配的快速性并降低误匹配的现象。同时对传统RatSLAM算法在动态环境中的适应性较差的问题作出改善，使得算法的鲁棒性变强。但是在仿真实验中也出现了因为实时匹配而导致的定位漂移的现象，这可以成为之后的实验研究重点，若能够实现突破，对于汽车自动驾驶方面将具有良好的应用前景。