BP神经网络在钢筋检测中的应用研究①

□□ 唐寿康，陈振富，2，吴文涛，罗志业，叶 涛，倪 康，王圳伦

(1.南华大学 土木工程学院，湖南 衡阳 421001； 2.高性能混凝土湖南省重点实验室，湖南 衡阳 421001)

引言

钢筋直径和保护层厚度的准确探测在工程检测和结构安全以及房屋加固和核电站膨胀螺栓安装管道设备中具有重要意义。张仁瑜[1]、应文武[2]和赵晖等[3]通过研究分析得出了电磁感应法检测钢筋保护层厚度的主要影响因素，其中包括：钢筋的间距，钢筋的疏密程度、排筋方式和仪器量程等都会对钢筋保护层厚度的检测产生较大的影响。目前国内常用且较为先进的无损检测钢筋混凝土构件中钢筋的方法是基于电磁感应的一体式钢筋扫描仪。张启明[4]采用钢筋保护层厚度测试仪检测钢筋保护层厚度时，指出测试仪中钢筋直径设置应和钢筋混凝土构件中的钢筋直径相同，才能保证保护层厚度测量的准确性，当测试仪中钢筋直径设置和钢筋混凝土构件中的钢筋直径误差相对较大时，所测的钢筋保护层厚度也越大。

为了进一步探索更加便捷的检测方法，本文使用模型模拟钢筋混凝土试件，并对其进行波形检测，经过对波形进行分析，便可得出钢筋的位置、钢筋直径以及保护层厚度。最后，通过对波形的分析获取描述波形的特征参数，使用波形的多个特征参数构建BP神经网络模型，建立复杂的非线性映射关系，以此模型来准确预测钢筋直径和保护层厚度，从而提高检测的准确度，推动检测的智能化发展。

1 检测试验前准备

1.1 仪器介绍

HC-GY71一体式钢筋扫描仪是利用电磁感应法原理，是国内检测钢筋保护层厚度较为先进的智能仪器。该仪器主要有厚度检测、估测直径、波形检测、JGJ检测、网格检测和剖面检测六个功能。但该仪器的缺点是在估测钢筋直径时需预先输入一个大致范围内的钢筋直径，在此基础上才能进行钢筋直径的估测。因此，需要对钢筋直径和保护层厚度精确检测进行进一步研究。

1.2 检测试件模型的制作

电磁感应法检测钢筋混凝土构件中钢筋是目前常用的无损检测方法，混凝土和空气等非磁性材料的磁导率是1，而钢筋等铁氧体的磁导率为104，磁导率的差异使得钢筋能够被识别和区分。此次试验是采用四块15 mm厚的木质胶合板制作正方形模板，模板两侧留置孔槽用来放置钢筋，模板上方放置透明玻璃，通过调节钢筋的橡胶或者木质垫块的厚度，来改变钢筋的保护层厚度，以此来模拟不同钢筋直径和保护层厚度下的钢筋混凝土试件，如图1所示。

图1 试件模型

2 试验方法

采用钢筋扫描仪波形检测公称直径为8 mm、12 mm、16 mm、20 mm、22 mm、25 mm、28 mm、32 mm、36 mm的钢筋，保护层厚度分别为15 mm、20 mm、25 mm、30 mm、35 mm、40 mm、50 mm、60 mm、70 mm，综合考虑不同钢筋直径和保护层，共81组试验组合，每组测三次波形。每扫描一次便可得到对应的波形图，如图2所示。横坐标为仪器扫描混凝土界面的宽度，单位为mm；纵坐标为仪器扫描处的信号强度。波形的中心红线，即波峰所对应的横坐标位置为所测得的钢筋位置，红线下方的数据为所测的钢筋保护层厚度。为便于对波形整体数据的分析，设定纵坐标的界限值统一为100，得到波形曲线上的具体数据，如图3所示。

图2 原始波形图

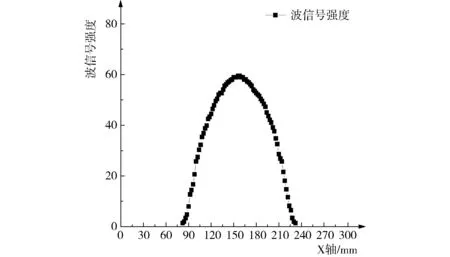
图3 处理后的波形图

3 试验结果与分析

3.1 峰值与波形宽度分析

图4为保护层厚度为30 mm条件下，钢筋公称直径分别为8 mm、12 mm、16 mm、20 mm、22 mm、25 mm、28 mm、32 mm、36 mm时对应的波形图。图5所示是钢筋公称直径为25 mm条件下，钢筋保护层厚度分别为15 mm、20 mm、25 mm、30 mm、35 mm、40 mm、50 mm、60 mm、70 mm时对应的波形图。

图4 波形随直径的变化图

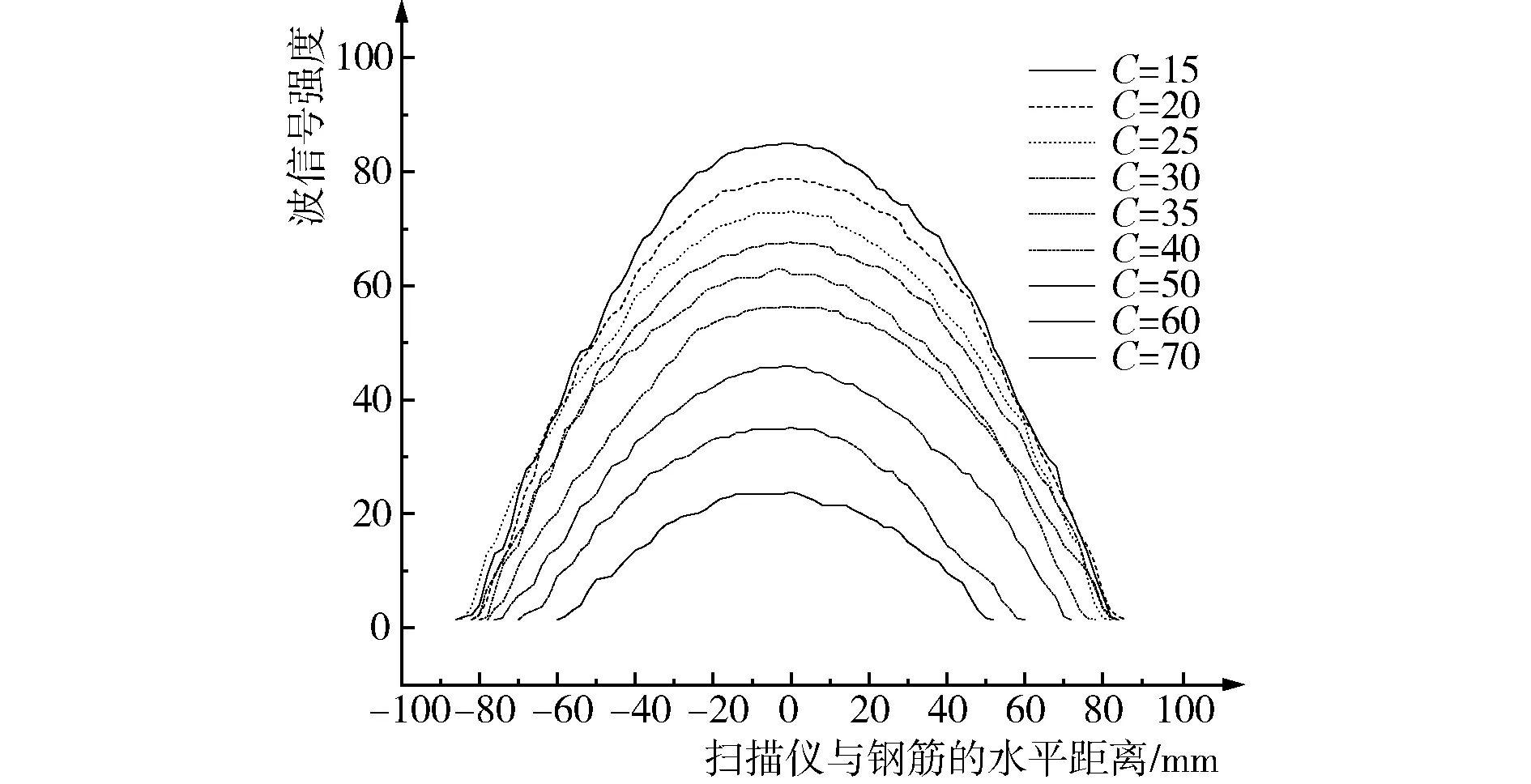
图5 波形随保护层厚度的变化

X轴为扫描仪与钢筋中心的水平距离，波形中心轴对应的位置X=0为钢筋中心点的位置，钢筋扫描仪自左往右扫描时，与钢筋的水平距离越大，波信号值越小。当钢筋中心与扫描仪的水平距离为0时，波信号值最大，此时对应的Y轴值即为峰值。每扫描一次得到一条波形图，波信号值为0所对应的X轴的宽度为波形宽度。

根据图4可以看出：在相同保护层厚度情况下，随着钢筋直径的逐渐增大，波信号强度也呈现出逐渐增大的趋势，但随着钢筋直径的继续增大，钢筋直径对波信号强度的影响却越来越小。且从图中可以明显发现，钢筋直径对波形曲率的影响相对较小。而从图5可以发现，在相同钢筋直径相同的情况下，保护层厚度同样对波信号强度有较大影响，随着保护层厚度的逐渐增大，波信号强度却逐渐减小，且波信号曲率也发生了明显变化，随着保护层厚度的增大逐渐减小。

为了更加直观地分析钢筋直径和保护层厚度对波信号强度以及波形宽度的影响，通过origin绘制钢筋直径和保护层厚度对波峰值的影响关系曲线，如图6和图7所示，绘制钢筋直径和保护层厚度对波形宽度的影响趋势图，如图8和图9所示，其中，钢筋保护层厚度为钢筋外缘到混凝土表面的距离。

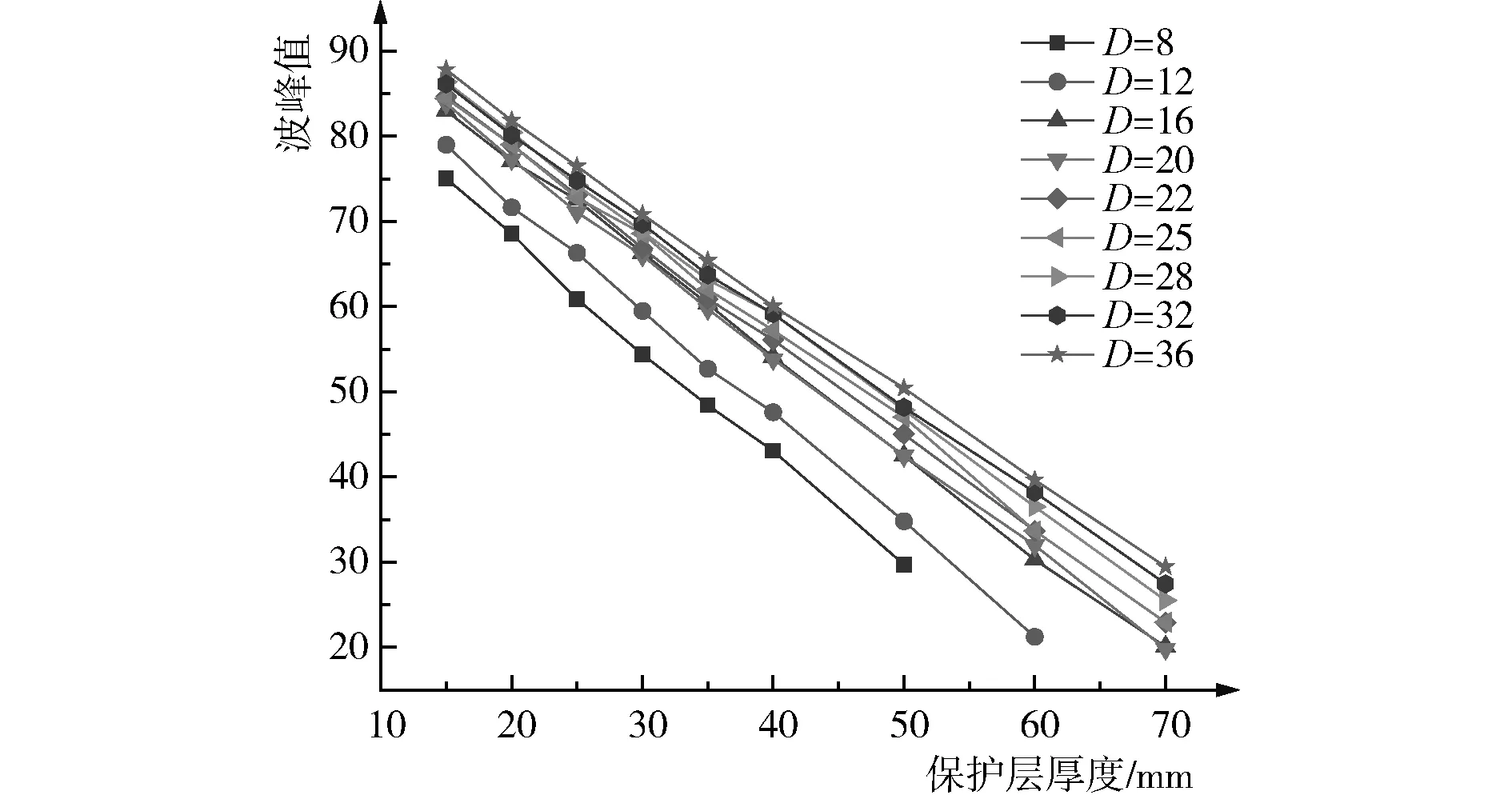
图6 峰值随保护层厚度的变化

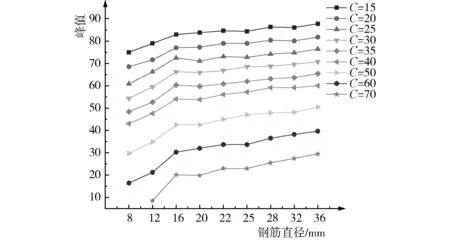
图7 峰值随钢筋直径的变化

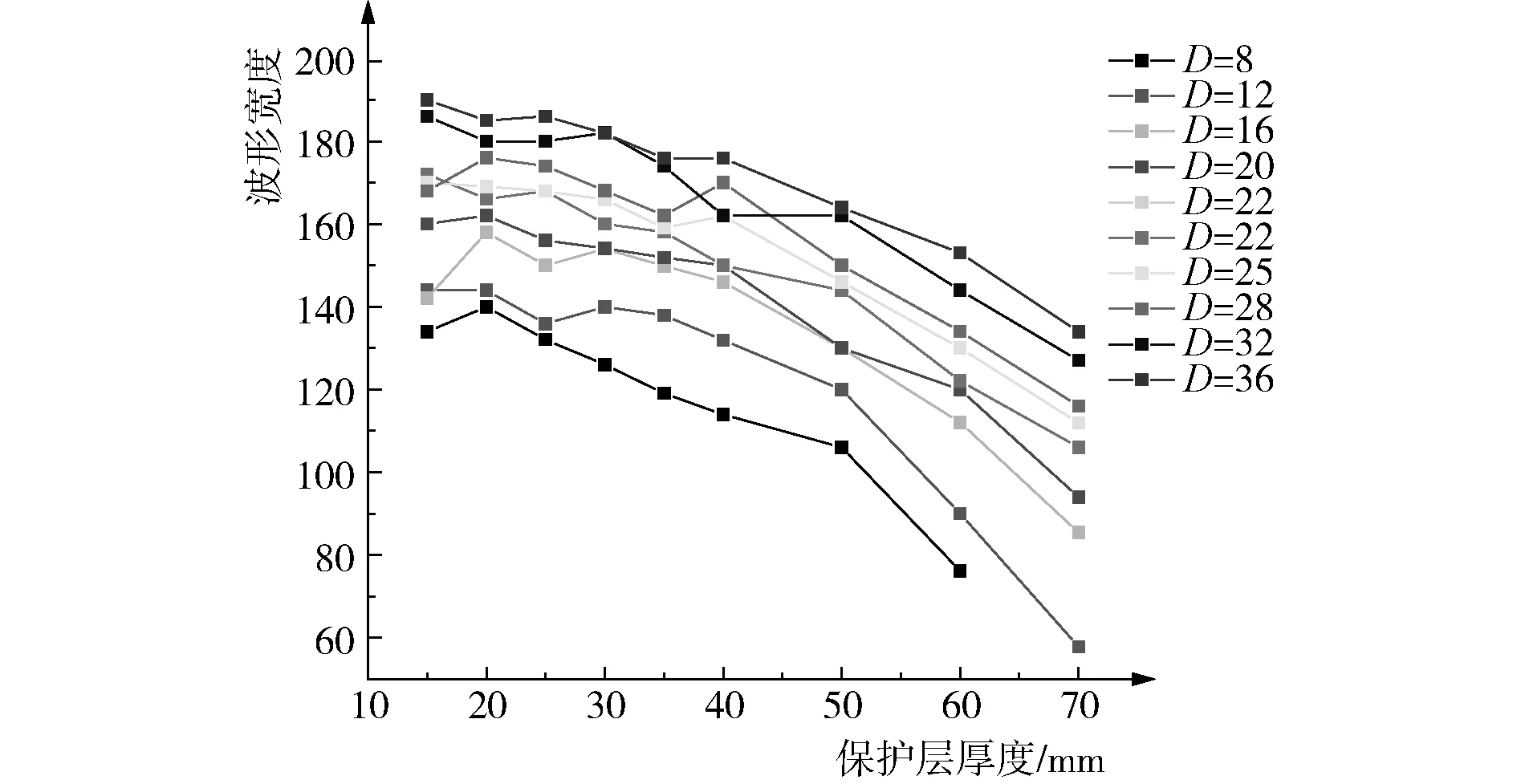
图8 波形宽度随保护层厚度的变化

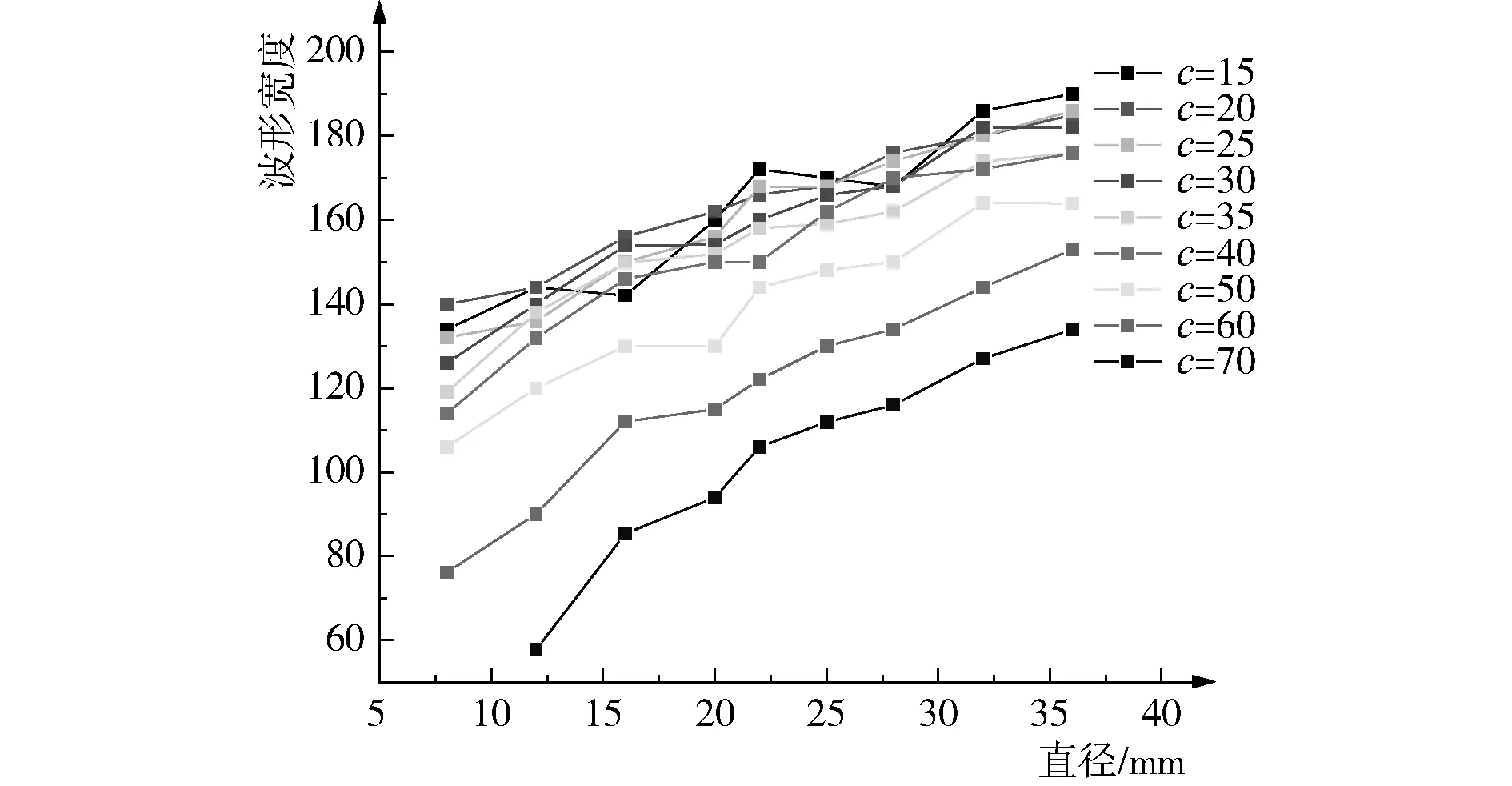
图9 波形宽度随钢筋直径的变化

从图6和图7可以发现，在相同的钢筋直径情况下，钢筋保护层厚度和波峰信号强度基本呈现出负线性相关性，即随着钢筋保护层厚度的增大，峰值逐渐减小。线性拟合相关系数都在0.99以上。在相同的保护层厚度情况下，钢筋直径和波峰信号强度呈现出了正线性相关性，即随着钢筋直径的增大，峰值也逐渐增大。

从图8和图9可以发现，在相同的钢筋直径情况下，钢筋保护层厚度和波形宽度基本呈现出负线性相关性，即随着钢筋保护层厚度的增大，波形宽度逐渐减小。在相同的保护层厚度情况下，钢筋直径和波形宽度呈现出了正线性相关性，即随着钢筋直径的增大，波形宽度也逐渐增大。

3.2 不同峰值下降宽度

以波信号强度为Y轴，扫描仪与钢筋的水平距离为X轴的波形图中(如图4和图5)，峰值下降3%的宽度即为：峰值下降3%后对应的Y轴波信号值所对应的X轴左右宽度值，以此类推峰值下降5%、8%、10%的宽度。

图10和图11分别为峰值下降3%和5%的宽度与保护层厚度的关系图，明显发现离散型程度较大，无法作为BP神经网络的特征参数。图12和图13分别为峰值下降8%和10%的宽度与保护层厚度的关系，其离散程度较小，随着保护层厚度的增大，峰值下降8%和10%的宽度也逐渐减小，线性拟合的相关系数R2都在0.9左右，因此峰值下降8%和10%的宽度可作为构建BP神经网络的特征参数。

图10 峰值下降3%的宽度与保护层厚度的关系

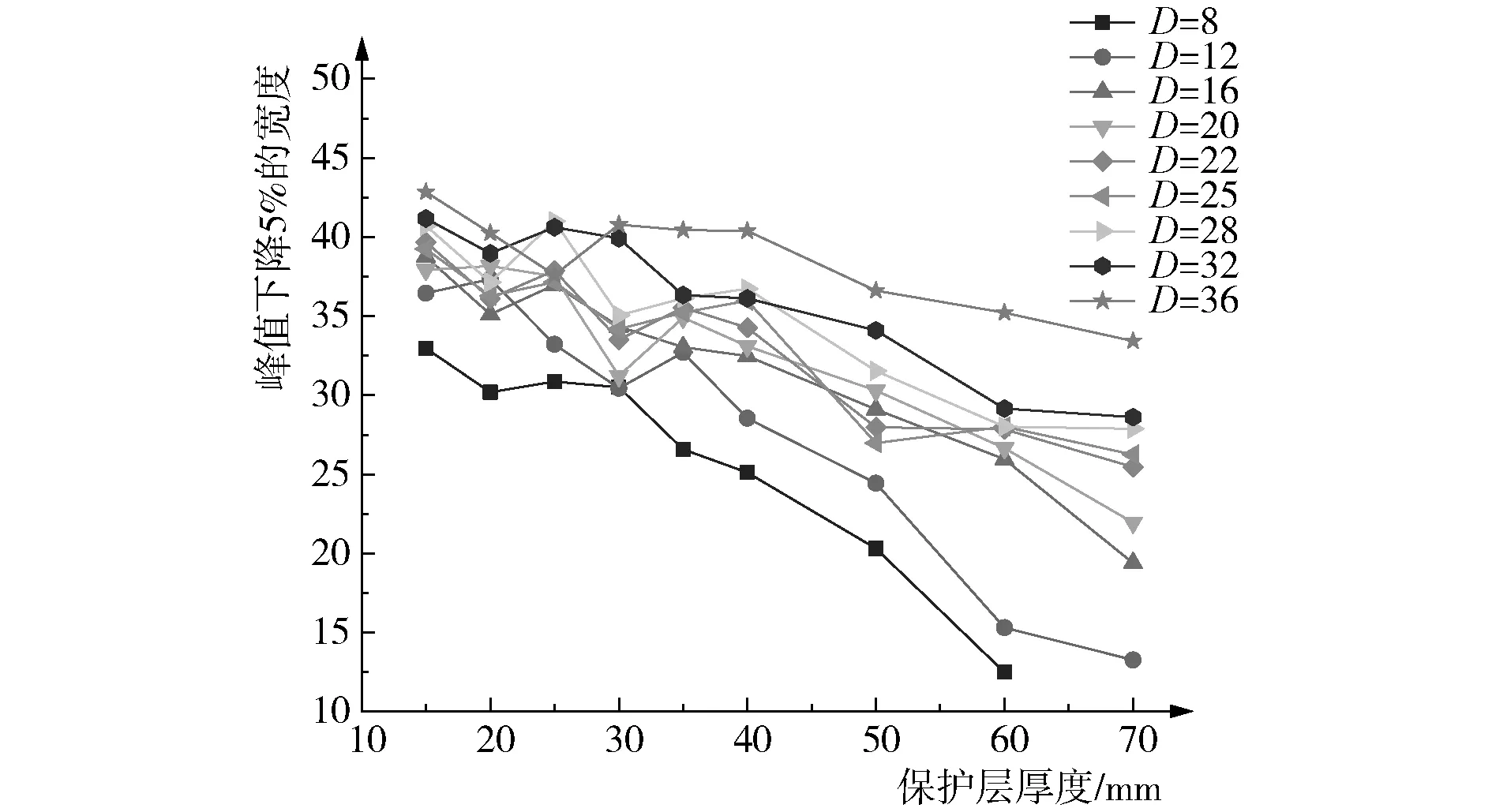
图11 峰值下降5%的宽度与保护层厚度的关系

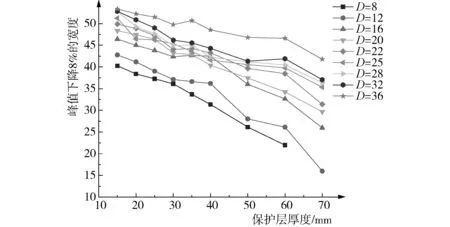
图12 峰值下降8%的宽度与保护层厚度的关系

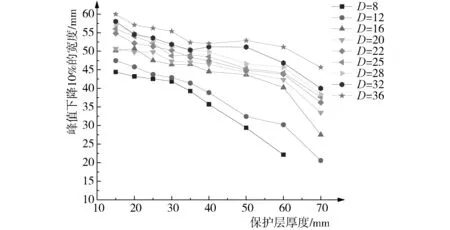
图13 峰值下降10%的宽度与保护层厚度的关系

3.3 波形数据曲线拟合

工程检测中，单根钢筋的波形往往会受到相邻钢筋的影响，无法获得单根钢筋的完整波形图，只能对波信号强度较大值的数据进行分析。利用波形峰值两侧对应X轴宽度为30 mm、50 mm和80 mm范围内的数据点进行拟合分析，拟合公式见式(1)。

f(x)=Ax4+Bx2+C

(1)

通过公式(1)拟合得到四次项系数A和二次项系数B。由于峰值两侧对应宽度30 mm的数据拟合效果较差，不能作为BP神经网络的特征参数。宽度50 mm和80 mm下拟合的相关系数R2都在0.95以上，拟合效果较好。实际工程检测中，由于存在多根钢筋的波形影响，选取50 mm宽度范围内的数据拟合得到的A和B作为构件BP神经模型的特征参数。

4 BP神经网络模型训练与预测

4.1 BP神经网络基本原理

人体大脑有大约1 000亿个神经网络，神经网络是仿真人体大脑里的神经元进行学习从而建立一较为复杂的映射函数关系。BP(Back Propagation)神经网络是由以Rumelhart和McCelland为首的科学家小组在1986年提出的一种按误差逆向传播进行算法训练的多层前馈网络，是目前最广泛应用的神经网络模型之一[5-6]。

BP神经网络是一个多层前向网络，常用的是三层网络结构。BP神经网络算法的基本思路是，学习过程由信号的正向传播和误差的反向传播两个过程完成。前向传播是通过将隐藏层逐步处理给定输入样本数据到输出层。当输出层的输出不等于预期输出或误差大，则将其传送到反向误差。

4.2 特征参数

此次创建网络样本的具体数据即为前面做的81组试验得到钢筋波形分析的五个特征参数：波峰值、波峰下降8%时所对应的宽度、波峰下降10%时所对应的宽度、峰值两侧宽度为50 mm范围内的数据公式(1)拟合的系数A和B等作为输入层的数据。钢筋直径和保护层厚度是需要获得的数据，即作为神经网络的输出值。

4.3 BP神经网络建立及结果分析

通过MATLAB编程建立BP神经网络数学模型。BP神经网络的输入特征参数为5个，输出参数是钢筋直径和保护层厚度。对训练样本归一化，初始化网络结构，设置网络参数：迭代次数、均方根误差率、学习率，均方根误差率是衡量误差有效的主要指标。网络参数的设置即是训练达到效果的重要保证。设置完参数之后则进行网络训练、预测和结果分析。

通过BP神经网络训练，得到样本均方误差的变化曲线，如图14所示。可看出，最优迭代次数是4次，在4次迭代后最好的训练结果是0.037 203。数据回归分析如图15所示，可看出，训练样本的误差平均平方随重复而降低，而验证样本和测试样本的误差平均平方也相应降低。

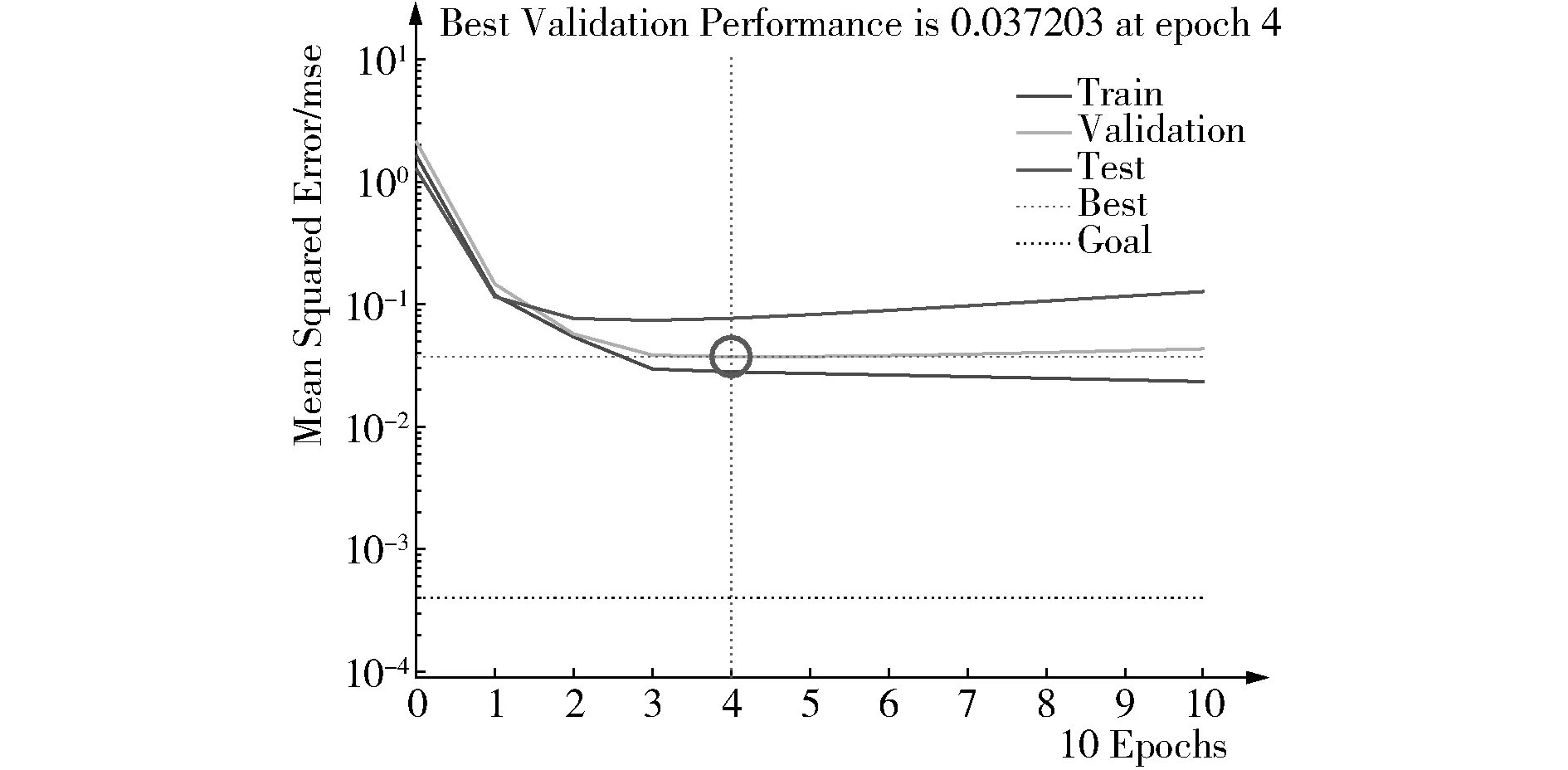
图14 样本均方误差的变化曲线

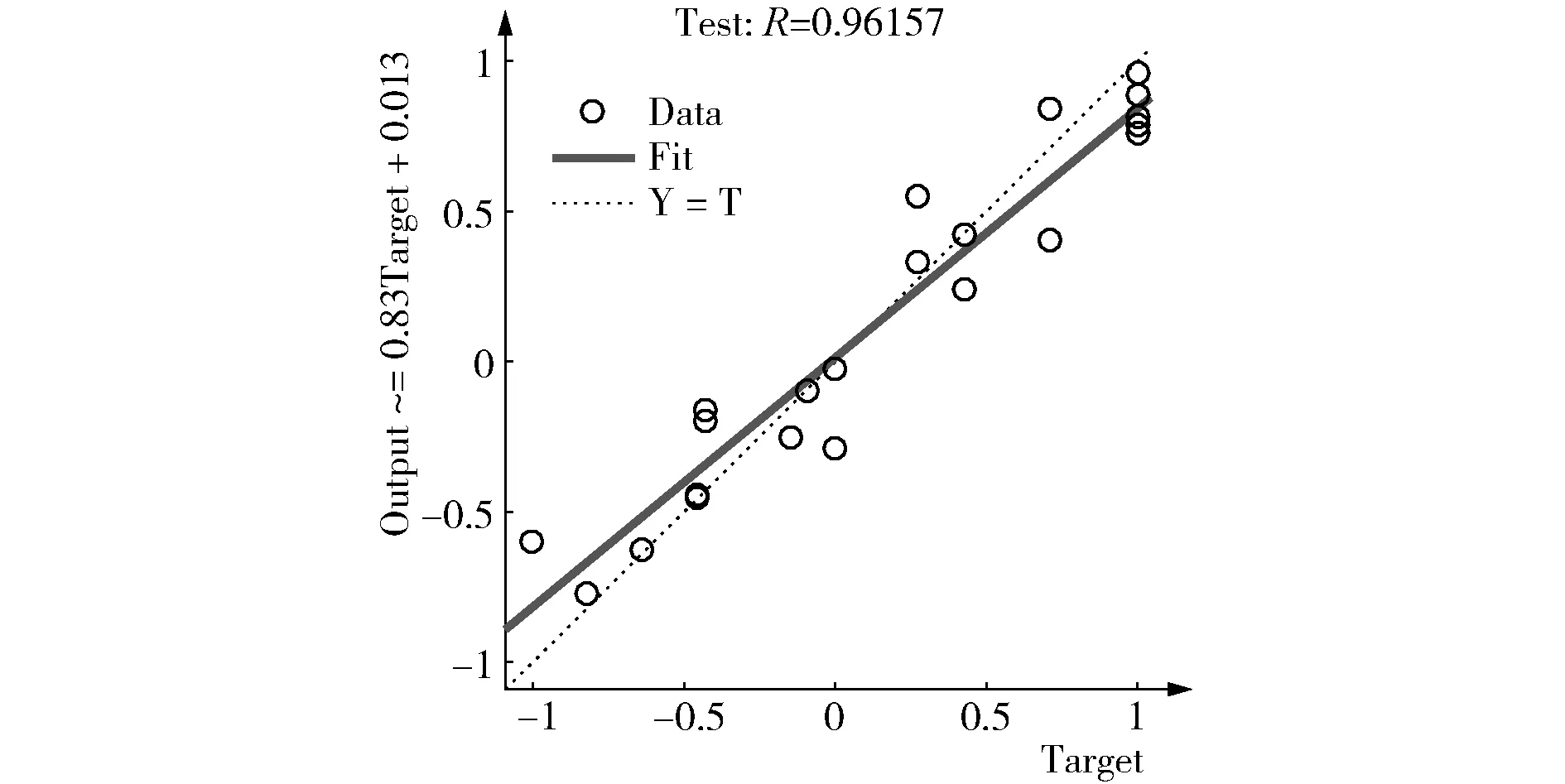
图15 回归分析

根据训练样本数据建立的BP神经网络模型得到钢筋直径和保护层厚度的预测值及误差见表1。由表1可知，钢筋直径的实测值与预测值的误差绝对值最大为1.794 9 mm，保护层厚度的实测值与预测值的误差绝对值最大为1.423 6 mm，预测误差较小，能满足工程的检测要求。

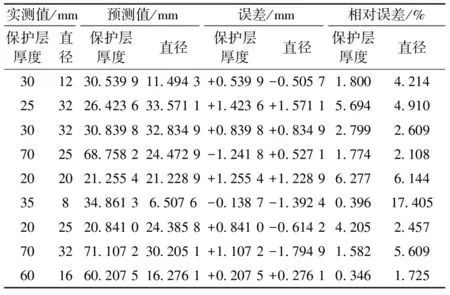
表1 BP神经网络对钢筋直径和保护层厚度预测的误差

5 结论

本文利用HC-GY71钢筋扫描仪检测出不同条件下的大量波形图，并将BP神经网络应用到钢筋直径和保护层厚度的预测中，得到以下结论：

5.1 通过对波形图数据分析，得到波形峰值与保护层厚度呈线性负相关，与钢筋直径呈线性正相关，线性拟合相关系数在0.99左右。波形宽度随保护层厚度的增大而减小，随钢筋直径的增大而增大。

5.2 对波形曲线峰值下降8%和10%的宽度分别进行分析，峰值下降8%和10%的宽度随着保护层厚度的增大而减小，拟合的相关系数为0.9左右；波峰对应宽度50 mm和80 mm的数据采用f(x)=Ax4+Bx2+C公式进行拟合，相关系数R2都在0.95以上，拟合结果较好。

5.3 以峰值、峰值下降10%的宽度、峰值下降8%的宽度、对应四次项系数A和二次项系数B作为BP神经网络的5个特征参数，BP神经网络模型预测的钢筋直径和保护层厚度误差基本能稳定在±2 mm以内，能满足钢筋检测的精准度要求，对提高检测水平有重要意义。