航天服充气压状态下的关节阻力矩特性研究

刘文樵，施 虎，谭 坤，张瑞明

(1.西安交通大学 机械工程学院，陕西 西安 710049；2.中国航天员科研训练中心，北京 100094)

引言

随着人类对太空探索的不断深入，人类在太空和其他星球的作业任务也越来越多。由于太空环境复杂、恶劣，航天员在开展空间作业任务时需要穿着特定的航天服。因此，航天服的活动性能对航天员的作业效率至关重要。通常航天员在穿上航天服之后，人体与航天服之间的封闭空间充入一定压力的气体以构成真空防护，导致航天服内外形成余压。

对于舱外作业而言，当航天员在作业过程中完成上肢和下肢弯曲运动时，此余压会导致航天服关节处产生相当大的阻力矩[1]，从而降低了航天员肢体运动的灵活度、准确性及平衡性，增加体能消耗，严重制约了航天员的舱外作业能力与活动范围[2]。因此，在设计制造阶段，通过理论建模实现对航天服运动力学性能的准确预测，不仅能够为航天员模拟训练提供理论参考，而且对于研制具有关节助力功能的航天服具有重要意义。由于航天服在充气压状态下属于柔性体，其运动与力学特性呈现出高度的非线性，难以直接建立数学描述模型[3]。基于实验测试的关节阻力矩和运动数据进行拟合建模是目前常用的研究方法。

在航天服关节阻力矩测试方面，目前国内外采用的测试方案主要分为内置式和外置式。内置式是目前在航天服工效学研究中采用的一种较先进的测量方法，如MIT采用内置式机器人RSST(Robotic Space Suit Tester)来测量EMU舱外航天服的关节阻力矩[4]，该方法由机器人直接驱动航天服各个关节运动，并由安装在机器人中的位置、力矩等传感器实时测量航天服各关节的转角和阻力矩，测量精度较高，能对航天服多个关节同时进行测量。但由于每个测试机器人只适合单一种类和尺寸的航天服，对于不同种类和尺寸的航天服则需要调整或重新设计测量装置，而且设备成本很高，可维护性相对较差，另外还会带来操作安全性和航天服内卫生等问题[5]。外置式则是研究最多使用最广泛的一种测量方法，目前外置式测量一般采用机械臂运动轨迹规划和转动轴自驱动扭矩测量2种方法。前者如哈尔滨工业大学的高志强等[6]提出的测量舱外航天服关节阻力矩采用外置式机器人，该方法需设计符合航天服关节运动特征的多自由度机械臂，并完成复杂的运动规划与动力学推导问题，针对不同关节需要重新规划，使得测量过程过于复杂化；而后者将航天服关节运动定义为沿固定转动中心的旋转运动，在转动轴处设置转动机构，使关节与身体连接一端固定，驱动转动机构并通过转动扭矩传感器测量关节阻力矩，这种方式方便且能直观测量关节力矩信息，如NASA[7-9]、中国航天员科研训练中心[10]均采用这种方法，但在目前的自驱动测量方法中，航天服关节并非有固定的转动中心，随着关节弯曲角度变化航天服转动中心会与机械机构转轴中心偏移，由此会造成测量误差。因此，基于以上方法的不足之处，本研究建立了一种通过简易的龙门模组滑台机构拟合航天服关节运动的测试平台。该平台通过拟合航天服关节弯曲运动轨迹，并由力传感器采集运动过程的驱动力信息，得到航天服关节阻力矩，具有设备操作、维护较为简单，可测量不同种类、尺寸的航天服的优点。

在航天服关节阻力矩的建模研究方面，由于舱外航天服关节材料和结构导致的迟滞特性，导致常规的数值拟合方法无法实现对阻力矩的准确描述[3]。目前国内外关于迟滞特性的研究主要是针对压电陶瓷等智能材料以及气动肌肉等驱动器件运动性能补偿控制方面[11-12]，典型的迟滞模型主要包括以Bouc-Wen模型为代表的微分型模型，和以Preisach模型为代表的积分型模型[13]。目前关于航天服关节阻力矩迟滞模型大多基于后者进行改进。SCHMIDT P B[14]、NEJMAN A J[15]基于Preisach模型建立了航天服关节阻力矩-角度模型。在国内，李照阳等[10]也选择使用Preisach模型描述航天服的迟滞特性；王晓东等[9]使用RBF神经网络建立了基于Preisach模型的航天服力矩-角度模型。但是通过参数辨识得到Preisach迟滞模型的方法需要考虑的参数较多，计算时间长，需要大量的训练才能使Preisach迟滞模型达到很高的精度[16]。念龙生等[17]提出了一种改进Preisach模型数值实现方法，为航天服关节阻力矩建模提供了新的思路。本研究通过结合改进Preisach模型数值实现方法与线性插值方法，建立了航天服关节阻力矩模型相较于参数辨识方法具有更大的便利性。

1 航天服关节阻力矩测试

1.1 测试原理

为了探究航天服关节在转动过程中的阻力矩特性，本试验方案采用了一种可以精确确定转动角度，精确施加牵引轨迹的测试方法，如图1所示。为了确保测试结果的准确性，试验过程中旋转中心和牵引力作用点及作用方向均不变。实际测试过程中，通过在如图2 所示的龙门模组结构中两垂直进给轴组成的测试平面内控制多组离散的运动轨迹点的位置来实现。

图1 测试原理示意图Fig.1 Schematic diagram of test principle

图2 航天服测试平台模型Fig.2 3D Model of spacesuit test platform

通过龙门式模台滑组Z轴向的滑台末端和关节牵引点连接，固定关节未活动一侧，利用控制器控制龙门模组滑台按照与力臂垂直的轨迹转动。由于龙门模组做圆弧插补时的线速度是匀速，因此关节的转动角度是与时间成正比的，同时由于航天服固定在测试平台上，其活动角度可由龙门模组坐标计算得到，由此可精确确定转动角度。通过测力计获得试验中的力数据后，关节力矩可以描述为：

M=F×L

(1)

式中，F—— 牵引作用点施加的力

L—— 力臂

M—— 牵引力对转动中心O的力矩

针对航天服活动过程中的具体力臂长度与转动中心难以准确确定的问题，该方法还可以对关节的转动中心进行精确测量。由于龙门模组可以通过圆弧插补的方式牵引航天服实现圆弧运动轨迹，因此可以利用关节旋转中龙门模组Z轴末端轨迹点的坐标推算出旋转中心和半径，同时也精确记录出旋转角度。在关节转动过程中，可以利用模组控制器精确的记录轨迹点坐标，再利用绘图软件，录入轨迹点坐标，可以拟合一条圆弧轨迹线，通过该圆弧轨迹反推确定出中心和旋转半径。

在试验平台方面，通过调整航天服位姿，使测试关节的活动平面与测试平台平行，以此抵消重力对试验的的影响，并通过固定卡箍将关节活动端固定在牛眼滑车上，以此来避免关节活动时肢体与测量平台的摩擦。

1.2 测试平台的搭建

为了进行航天服关节力矩测试，结合航天服和测试场地条件自主研制了航天服力矩测试平台，如图2所示。该平台主要由航天服支撑调整架、测试平面及支撑架、龙门模组及控制系统、充压系统和测力系统等组成。

航天服固定支架及调节机构是进行航天服测试的基础，其主要功能是以航天服躯干侧销座和前销钉座为连接固定点，夹持固定航天服，并调整航天服的位姿。固定的航天服可以侧向翻转，与水平面平行。测试平面安装于支撑架上，并配置一台牛眼滑车用于消除摩擦对试验结果的影响。根据牛眼滑车性能参数可知，其万向滚珠平均摩擦系数为0.010～0.015，且航天服内为中空充气状态，牛眼滑车竖直方向上承受的作用力小于50 N，因此该摩擦力可以忽略不计。同时为了使关节在尽可能水平面内活动，不受重力干扰，应保证牛眼滑车高度与固定卡箍内圈最低点相同。龙门模组滑台主要由4组丝杠螺母副组成，并由步进电机及电机驱动器进行驱动调节，由于步进电机启停换向速度较快，因此对试验结果的影响可忽略不计。滑台两端设有限位传感器，便于滑块模组的找零位。选用如图3所示的PAC可编程自动化控制器作为龙门模组的控制系统，航天服关节的主要运动是圆周轨迹运动，使用此控制器可通过圆弧插补指令实现该运动轨迹。

图3 PAC可编程自动化控制器控制面板Fig.3 PAC programmable automation controller panel

本试验采用OTS-750x2-50L静音无油空气压缩机作为气压发生装置，提供给航天服所需要的试验内压强环境，试验时需要先通过顶端的开关给压缩机充入气体，然后再将气体从压缩机通过气体管路充入航天服内。最终以航天服上压力表作为充压是否结束的衡量标准，设定试验所需的压力。同时为了系统的安全考虑，设置了快速泄压装置作为试验保障。

测试现场如图4所示。测力系统主要采用LMN-6850型手持式测力仪。试验时，龙门模组通过测力传感器带动航天服关节运动，并实时进行数据采集与存储。同时，该测力计由螺栓通过横向插入方式与航天服关节处的卡箍连接，由此保证测量过程中拉力计与航天服力臂垂直，如图4a所示。

图4 现场试验图Fig.4 Field test

1.3 测量步骤及结果分析

本次试验主要测试了航天服的肘关节、膝关节、髋关节，如图5所示，具体测试步骤为：将航天服固定于支撑架上，通过航天服调节机构调整航天服的高度和位姿，使得航天服测试关节平行放置在测试平板上，抵消重力影响；通过压缩机给航天服充压，得到不同余压测试环境；通过固定卡箍将关节不动端固定在测试平板上，通过固定卡箍将关节活动端固定在牛眼滑车上；将龙门滑组的Z轴立柱与关节活动端的固定卡箍通过测力传感器相连，通过龙门滑组进行圆周运动带动关节进行相应的圆周运动；并通过测力计上位机软件实时采集关节力数据。

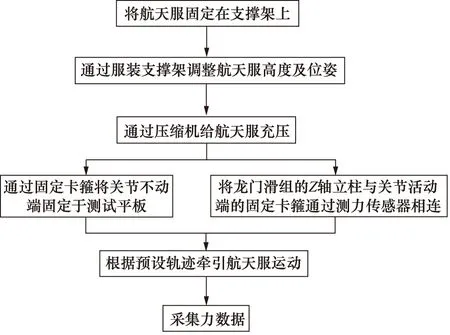
图5 测量步骤Fig.5 Measurement steps

为探究航天服余压及关节活动速度对关节阻力矩的影响，设计了2组试验。

第1组试验为相同关节活动速度、不同航天服余压条件下的测量。由于航天服的最低工作余压为0.010 MPa，登月服的工作余压为0.025 MPa，正常舱外航天服的工作余压为0.040 MPa，因此分别测量肘关节、膝关节、髋关节在这3种余压条件下活动时的关节力矩。其中，测量肘关节时，龙门模组丝杠速度为600 mm/min，关节从0°活动至最大角度再活动至0°共测量12个周期，初始最大测量角度为60°，每个周期的最大角度以5°递减；测量膝关节时，龙门模组丝杠速度为1000 mm/min，关节从0°活动至最大角度再活动至0°共测量13个周期，初始最大测量角度为65°，每个周期的最大角度以5°递减；测量髋关节时，龙门模组丝杠速度为600 mm/min，关节从0°活动至最大角度再活动至0°共测量8个周期，初始最大测量角度为40°，每个周期的最大角度以5°递减。阻力矩大小随时间变化的关系如图6所示。

图6 不同气压下各关节阻力矩随时间变化关系Fig.6 Relation of resistance moment of joints with time under different air pressures

第2组试验为相同航天服余压、不同关节活动速度条件下的测量。将航天服余压控制在0.040 MPa，并分别测量了肘关节、膝关节、髋关节在不同活动速度条件下活动时的关节力矩。其中，测量肘关节时，龙门模组丝杠速度分别为1000, 1400 mm/min，关节从0°活动至最大角度再活动至0°共测量12个周期，初始最大测量角度为60°，每个周期的最大角度以5°递减；测量膝关节时，龙门模组丝杠速度分别为600, 1000 mm/min，关节从0°活动至最大角度再活动至0°共测量13个周期，初始最大测量角度为65°，每个周期的最大角度以5°递减；测量髋关节时，龙门模组丝杠速度分别为600, 1000 mm/min，关节从0°活动至最大角度再活动至0°共测量8个周期，初始最大测量角度为40°，每个周期的最大角度以5°递减。阻力矩大小随时间变化的关系如图7所示。

图7 不同速度下关节阻力矩随时间变化关系Fig.7 Relation of resistance moment of joints with time at different speeds

在这2组试验中，关节活动角度的增加阶段与减小阶段关节力矩变化均出现了不对称，体现出了明显的迟滞特性。同时，在航天服关节活动的过程中，当关节角度从极限位置减小到某一个值时，航天服便无法靠自身弹性恢复到初始位置，此时为了使航天服继续活动，需要对航天服施加一个相反方向的力。由第1组试验结果可知，关节阻力矩大小与航天服余压正相关，航天服余压越大关节阻力矩也越大，而由第2组试验结果可知，关节阻力矩与关节活动速度无明显关系。

2 航天服关节阻力矩迟滞特性建模

在获得航天服肘关节、膝关节、髋关节的关节阻力矩试验数据后，本研究采用迟滞模型中较为经典的Preisach模型进行建模，并在其基础上提出了通过结合改进的Preisach数值实现方法与线性插值来实现该模型的方法。

2.1 Preisach模型原理

经典Preisach模型由Ferenc Preisach为解决铁磁材料中的迟滞现象而提出，由多个具有不同权重的基本迟滞变换函数叠加构成，其数学表达式为：

(2)

其中，u(t)表示t时刻输入的角度；M(t)表示t时刻输出的力矩；γα,β为基本迟滞变换函数，α和β(α>β)分别表示输入向上和向下变换的变换点，在该模型中，基本迟滞变换函数的值为1或-1；α和β分别是航天服关节弯曲过程中的角度增加量和减小量；μ(α,β)是γα, β的权重函数。

目前关于航天服关节力矩的研究中普遍使用了参数辨识的方法对权重函数μ(α,β)进行辨识，该方法需要大量训练样本，耗时较多，精度较难保证。采用线性插值拟合的数值实现方法可以很好解决这一问题。

经典Preisach模型具有擦除性和一致性2个特性，一致性指的是极大值与极小值相等的闭合迟滞曲线一致，擦除性指当输入大于历史上的极大值或者小于历史上的极小值时，模型会擦除这些历史极值，以新的输入为极值。

2.2 航天服迟滞特性建模

经典的Preisach模型数值实现方法不具有擦除特性，当输入大于历史极大值或小于历史极小值时，经典数值实现方法的计算结果与模型实际输出值有较大误差，因此无法适用于输入变化过程较为复杂的场景。为了解决此问题，念龙生等[17]在原有的Preisach数值实现方法基础上，通过加入历史极值数组，提出了一种具有擦除特性的改进Preisach数值实现方法，其具体表达式如下：

(3)

其中，数组α和β分别为极大值递减数列和极小值递增数列，在角度增加阶段与减小阶段转换时，将极大值和极小值分别存储在极大值数组和极小值数组中，使该实现方法具有记忆性；n与数组大小相关；u(t)为实时输入角度值，u′(t)为输入角度的导数，α′,β′为数组α和β中的值；擦除函数g1和g2分别不断更新数组α和β及n，使这个数值实现方法具有擦除特性。

为了便于预测航天服关节在活动过程中输出的力矩，首先将Preisach平面离散化，如图8所示。然后通过试验获得航天服余压为40 MPa时，关节从初始位置活动至等分满程角度所输出的力矩，建立离散平面上每个节点对应的α-β插值曲面，如图9所示。

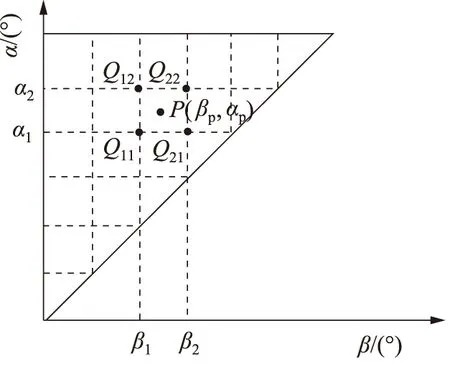
图8 离散化的Preisach平面Fig.8 The discretized Preisach plane

图9 各关节上升角度α、下降角度β与力矩关系Fig.9 Relationship between ascending angles α and descending angles β of each joint and torque

对于航天服活动过程中任意不处于等分点上的力矩-角度点P(βP,αP)，由双线性插值法原理可得：

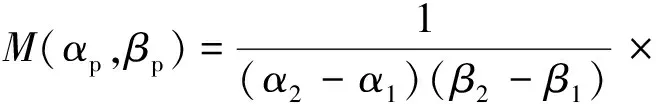
(4)

由式(4)可求得任意一点的输出力矩。具体流程如图10所示，在对模型进行离散化以后，当模型接收到输入角度时，首先判断输入角度相比上一个输入角度是增加还是减小，完成极值数列的更新；然后依据数组信息辨识该输入角度在离散Preisach平面上所处的位置，进行双线性插值，求解出该输入角度值所对应的输出力矩值；最后输出力矩值，完成一次对应求解。

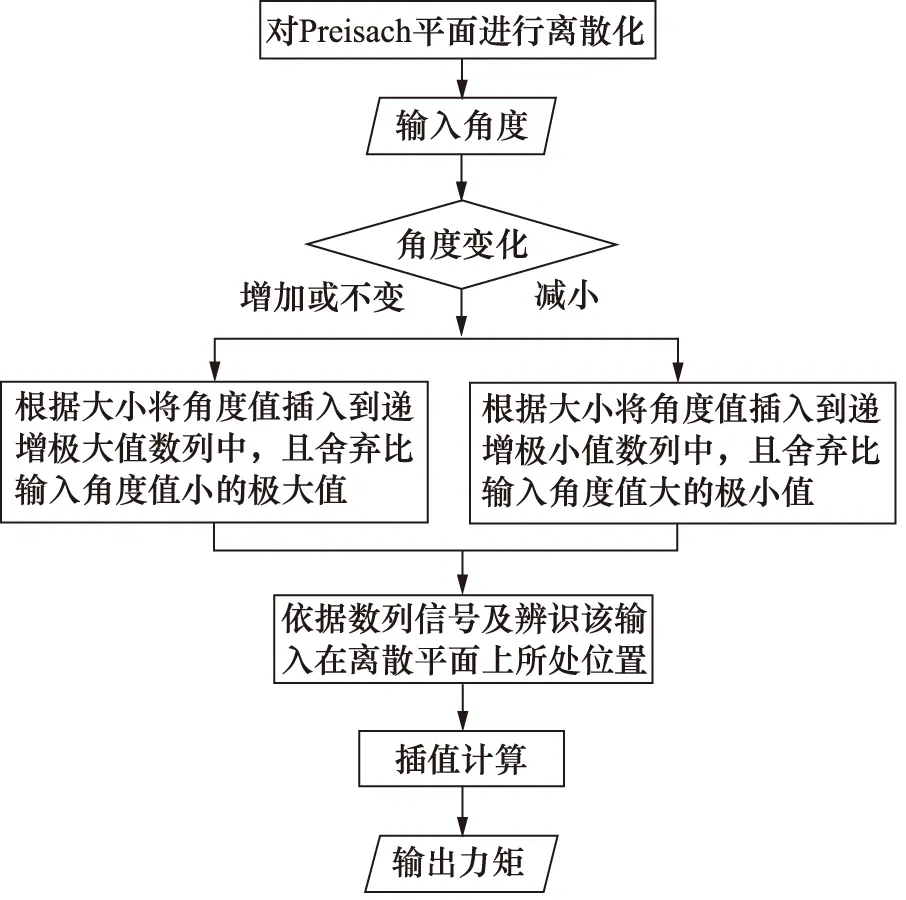
图10 模型求解流程

2.3 模型验证

依据上述模型实现方法，通过MATLAB/Simulink建立航天服关节模型，如图11所示。将关节的活动范围输入到模型中，在该仿真中，各关节活动范围分别为：肘关节0.14 °～46.74 °，膝关节0 °～24 °，髋关节0 °～16.91 °。 将得到各关节的仿真力矩与试验测得的关节力矩进行比较，结果如图12所示。通过仿真结果与试验测量结果的比较，肘关节与髋关节的仿真关节阻力距变化与试验数据较为吻合，膝关节的仿真力矩在关节活动至18°时随时间的增加较慢。3个关节活动过程中仿真力矩大小与试验数据的平均相对误差分别为：肘关节3.41%、膝关节6.02%、髋关节0.75%。仿真模型对肘关节、膝关节、髋关节活动中的关节阻力矩预测值基本与试验数据吻合，力矩变化趋势基本一致，因此，该仿真模型能有效预测航天服关节活动阻力矩。

图11 Simulink仿真模型

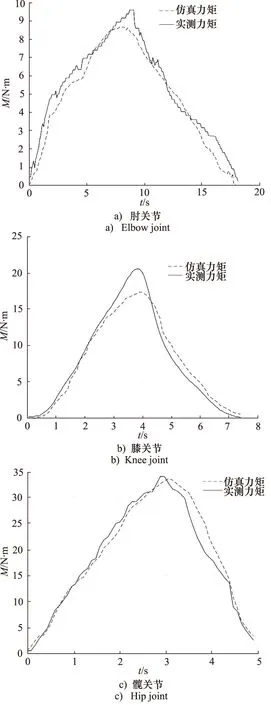
图12 各关节仿真力矩与实验力矩对比Fig.12 Comparison of joint torques obtained by simulation and experiment

3 结论

(1) 本研究在分析舱外航天服关节阻力矩特性的基础上，研制了一套航天服关节阻力矩测试平台，通过拟合航天服关节弯曲运动轨迹，并由力传感器实时采集关节驱动力，得到航天服关节阻力矩，该平台结构简单，操作方便，可适用于不同种类、尺寸的航天服，在该平台上开展了航天服运动特性、力学特性测试，测试结果表明，关节阻力矩大小与航天服余压正相关，航天服余压越大关节阻力矩也越大，而关节阻力矩与关节活动速度无明显关系；

(2) 提出了一种基于双线性插值的Preisach模型数值实现方法，基于试验数据建立了航天服关节阻力矩迟滞模型，相较于常规的参数辨识方法，本研究改进的迟滞模型具有求解速度更快，所需试验数据样本更少的特点，模型预测与测试对比结果表明，模型能有效预测服装关节活动阻力矩，肘关节的平均相对误差为3.41%、膝关节的平均相对误差为6.02%、髋关节的平均相对误差为0.75%，为航天服运动力学性能的准确预测提供了理论支撑。