星间激光通信中四象限探测器的定位精度研究

李树德,刘彩霞,徐 林,安建欣,刘 政

(1.桂林航天工业学院 电子信息与自动化学院，广西 桂林 541004；2.中国电子科技集团公司第三十四研究所，广西 桂林 541004)

0 引 言

随着空间技术的发展，各类高带宽仪器在卫星上得到大量应用，使得对卫星信息传输量的需求呈指数级增长[1]。星间激光通信技术因其传输容量大、发射功率小和抗干扰能力强等诸多优点，正成为大容量和高码率卫星通信的理想选择。

由于星间激光通信距离远，激光发散角小，为建立可靠和稳定的通信链路，需要“捕获—对准—跟踪”(Acquisition Pointing and Tracking，APT)系统达到微弧度量级的跟踪精度才能完成。而精跟踪探测器的光斑定位精度决定着APT系统的最终跟踪精度[2]，是通信链路建立的关键。从探测频段、探测带宽和性价比上来讲，四象限探测器(Four-Quadrant Detector，FQD)都是精跟踪探测器较为理想的选择[3]。因此，为了精确获取光斑的位置，有必要对FQD定位精度的误差分配进行详细地研究与分析。

针对FQD的定位误差问题，文献[4]用实验的方法确立了定位误差与输出电压的关系，但并未明确定位误差的来源；文献[5]具体分析了可能引起定位误差的噪声因素，但并未对影响程度进行评估；文献[6]针对大气激光通信分析了影响FQD定位精度的误差来源，但未考虑星间通信的情形。本文将结合星间光通信的实际，分析影响FQD定位精度的各类噪声因素，并从误差分析的角度给出具体的误差计算公式，最后通过算例评估各类因素对定位精度的影响程度。

1 定位原理

1.1 FQD的工作原理

FQD是一种位置敏感型光电探测器，其光敏面由4个完全相同的光电二极管按照一定顺序排列组成，形成4个象限区域A、B、C和D，如图1所示。当光束入射到光敏面时，4个象限所感受到的光能量不同，所形成的光电流大小也不同。通过比较光电流大小可确定光斑中心相对于FQD原点的偏移量。

图1所示为光斑脱靶图，当激光束成像于FQD的光敏面上时，光斑(如图1中阴影部分所示)在4个象限上被分成4个部分，每个象限产生对应的光电流，光电流大小可通过测量电路较容易获得。此时可定义水平脱靶量σx和垂直脱靶量σy如下：

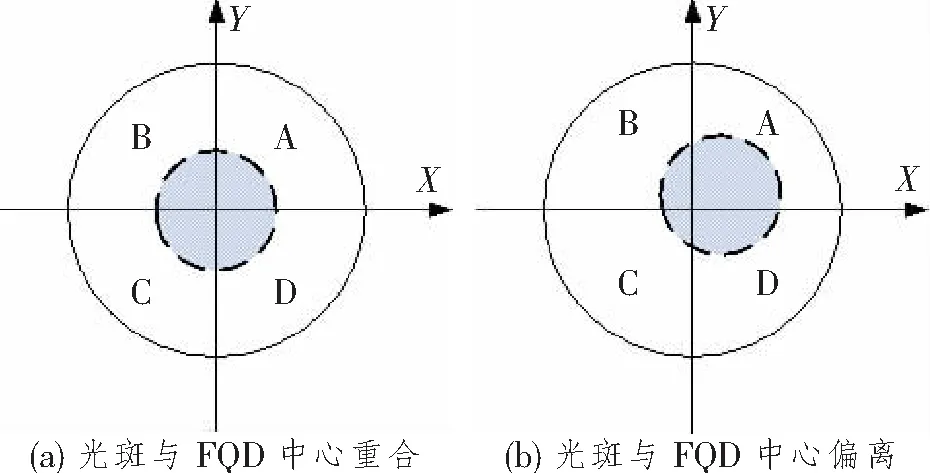
图1 光斑脱靶图

式中：SA、SB、SC和SD分别为光斑在4个象限的面积；EA、EB、EC和ED分别为4个象限所接收到的光能量；IA、IB、IC和ID分别为对应的4个象限所产生的光电流。由式(1)可知，脱靶量的大小由各象限光电流的大小决定，光电流的大小取决于每个象限所感受到的光能量，而该光能量是每个象限的光斑面积与光能量分布的加权积分[7]：

式中，φ(x,y)为光斑能量分布密度。显然，由式(1)和(2)可知，函数fi()的形式与光斑能量分布及光斑中心水平偏移量x和垂直偏移量y的大小相关，而x和y正是确定FQD定位精度所必需的参数。

1.2 脱靶量σx、σy与光斑中心实际偏移量x、y的 关系

在星间光通信中，通信用激光光束的发散角较小，但由于通信距离较远，到达接收端的光斑面积已变得非常大。接收端光学系统受制于体积的限制，其接收孔径一般≤200 mm，远小于接收端光斑半径。在这一较小的接收面积上，光斑的能量分布变化不大，因此可假设光斑的能量分布为均匀分布，即其光斑能量分布函数可假定为常数，以此为基础对式(1)进行简化和推导可得：

式中，r为光斑半径。

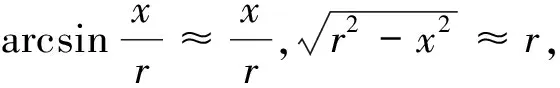
同理可得：

即

由式(4)可知，在假定光斑能量分布满足均匀分布的情况下，光斑实际位置偏移量x和y与光斑脱靶量σx和σy间具有近似的线性关系。

2 FQD定位精度分析与计算

2.1 定位误差解析

FQD的信噪比(Signal-to-Noise Ratio，SNR)定义为均方根信号光电流与均方根噪声光电流之比。在相同的信号光辐射功率下，SNR越大说明FQD性能越好。FQD在实际使用过程中受制于环境和探测器自身的特性，光电流的测量值通常是真值与噪声值的叠加。由于σx和σy具有相同的特性，下面将以σx为例进行分析。

根据上文分析可将A和D象限光电流之和IAD及B和C象限光电流之和IBC表示为

式中：IADr和IBCr均为光电流真值；εAD和εBC均为FQD的噪声值。

当不考虑噪声影响且目标被瞄准在FQD中心时，可假设IADr=IBCr=I，即

但在实际使用时，受噪声因素影响，σx≠0且εAD、εBC≪I，即满足下式：

式中，εAD和εBC可看作具有相同分布函数且相互独立的随机变量，其方差均为Dε，Dε=E(ε2)，则随机变量σx标准差为

由式(8)可知，σx的标准差只与SNR有关。因此，如果已知SNR，即可联合式(8)和(4)求得光斑水平偏移量x。垂直偏移量y计算方法类似。

2.2 噪声分析与测角精度计算

FQD的光敏面是由4个完全相同的光电二极管组合而成，因此可以引用光电二极管的等效电路来计算FQD的噪声来源。

图2所示为FQD等效电路图，图2(a)为考虑到光电二极管结构和功能后画出的微变等效电路，其中IP为信号光电流；IF为暗电流；Cf为结电容；Rsh为漏电阻；RS为串联电阻；RL为负载电阻。低频情况下，图2(a)可简化为图2(b)[9]。

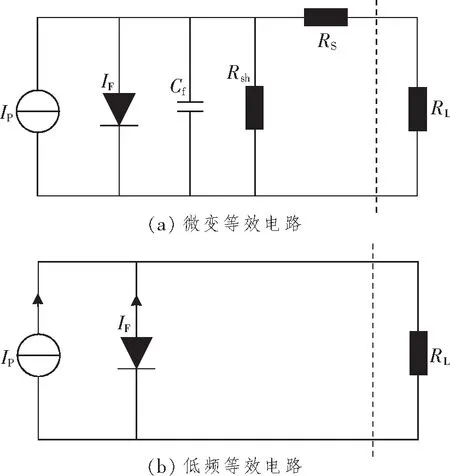
图2 FQD等效电路

FQD常见尺寸有Ø0.5、Ø1.0和Ø3.0等，光敏面面积较大，高频特性不好，因此可用低频等效电路来分析其噪声特性。在星间光通信中，FQD主要有两个噪声来源：热噪声和散粒噪声。其中散粒噪声又包括信号光电流噪声、背景光电流噪声和暗电流噪声。热噪声主要为负载电阻产生的热噪声。噪声电流计算公式如下：

式中：K为波尔兹曼常数，为1.38×10-23J/K；T为FQD的绝对温度；IE为背景光电流；Δf为FQD电路带宽。

下面以OSI公司的FCI-InGaAs-Q1000型FQD来分析噪声计算过程，其性能参数如表1所示。

表1 FCI-InGaAs-Q1000主要参数

假定FQD电路带宽为1 MHz，光电响应为0.9 A/W，信号光波长λ采用1 550 nm，光束发散角为10 urad，信号光/信标光分光比为9∶1，通信距离约20 000 km，温度为室温25 ℃，背景光功率为10-11W[10](采用窄带滤光片)，接收孔径为250 mm，接收光路系统焦距为1 000 mm，负载电阻取100 kΩ，e为1.6×10-19C，K为1.38×10-23J/K。表2列出了在发射功率为1 W的情况下，由信标光电流噪声所引起的光斑定位误差及精跟踪单元测角误差的计算方法及计算结果，其他发射功率下的计算方法相同。

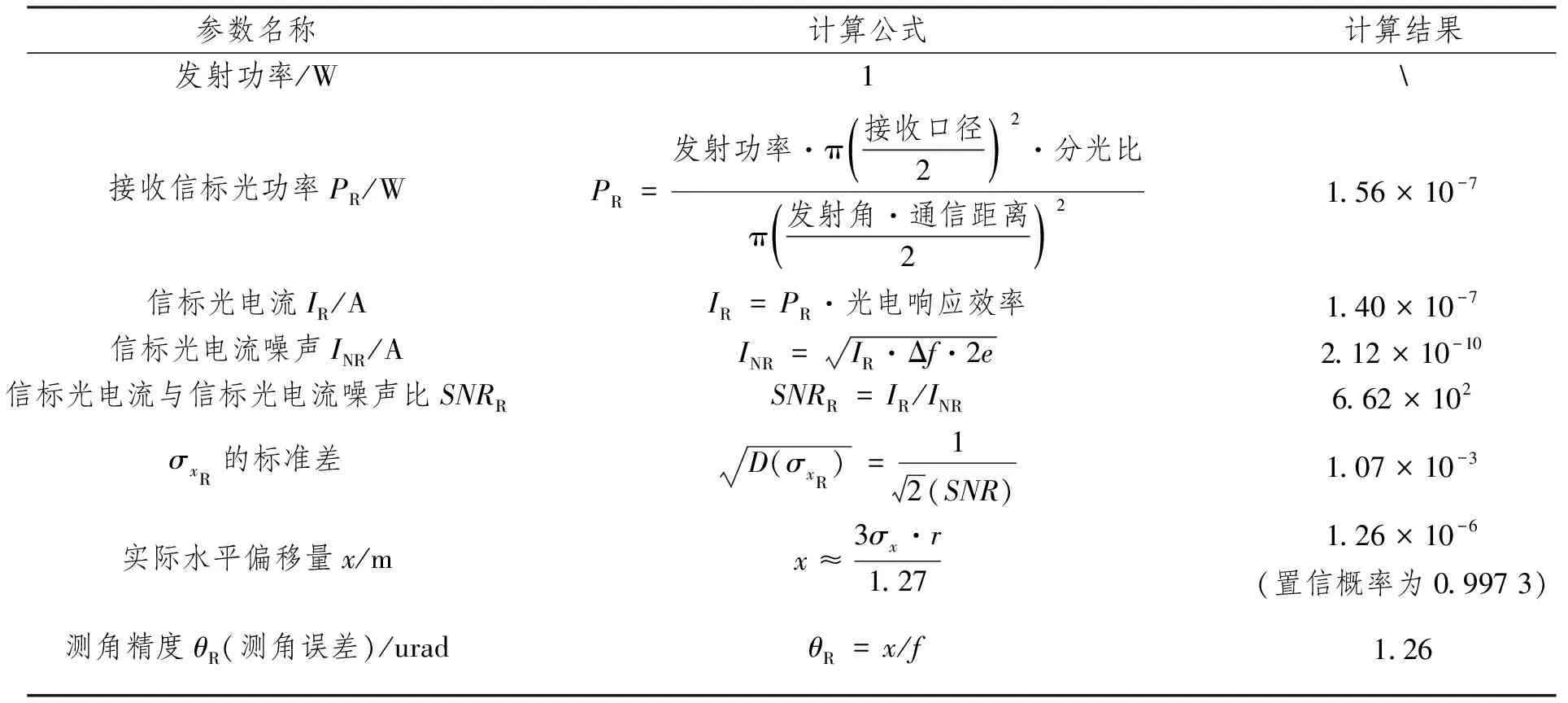
表2 信标光电流噪声引起的测角误差计算

采用与表2相同的方法，可计算不同发射功率下其他各个噪声源所引起的测角误差。不同发射功率下，信号光电流噪声、暗电流噪声、背景光电流噪声及热噪声引起的测角误差如图3所示。

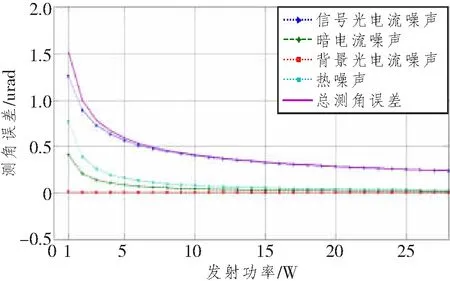
图3 不同发射功率下各噪声源 引起的测角误差的变化趋势

不同发射功率下，信号光电流噪声、暗电流噪声、背景光电流噪声及热噪声引起的测角误差对总测角误差的贡献比如图4所示。图中，L区域为信号光电流噪声贡献比，M区域为暗电流噪声贡献比，N区域为热噪声贡献比。

图4 不同发射功率下各类噪声源 对测角误差的贡献比

由图3和4可知，随着发射功率的增加，不同噪声源引起的测角误差都有一定程度的减小，但各类噪声源对测角误差的贡献比是不同的，其中，信号光电流噪声的占比最大，热噪声和暗电流噪声依次递减，背景光电流噪声可忽略不计。由图还可知，提高发射功率可以在一定范围内提高接收端信号的SNR，进而减小FQD的光斑定位误差，提高测角精度。但是，定位误差并非随发射功率的增大而线性减小，当发射功率增大到一定程度(如图中的10 W)后，定位误差的减小有限，这时再单纯通过增大发射功率来提高测角精度，代价将非常大。

3 结束语

FQD因其良好的性能和出色的性价比成为星间光通信中光斑定位的首选传感器之一。但由于各类噪声因素的影响，其定位精度受到一定的限制。本文基于星间光通信的实际，从噪声的角度分析了影响FQD定位误差的因素，并通过计算评估了不同噪声因素的影响程度。研究结果表明，提高发射功率可以在一定范围内提高FQD的SNR，进而提高定位精度，但是超出一定范围后，效果有限，代价巨大。因此，为提高FQD的定位精度，除适当增大发射功率之外，还应从提高探测器的灵敏度、象限一致性、机械安装精度和光源质量等方面出发，研究提高FQD定位精度的方法与措施。