一种低原子序数元素EDXRF的多次导-样条小波解析方法研究
吴廉晖,何剑锋*,周世融,汪雪元,叶志翔
1. 东华理工大学放射性地质与勘探技术国防重点学科实验室,江西 南昌 330013 2. 东华理工大学江西省放射性地学大数据技术工程实验室,江西 南昌 330013 3.东华理工大学信息工程学院,江西 南昌 330013
引 言
能量色散X荧光分析(EDXRF)技术具有多元素无损测定、 快速便携、 安全可靠等优势,引起了矿山采选冶、 地质勘探、 合金分析检测等诸多领域的广泛关注与应用[1]。其中,X荧光光谱的重叠峰分解是至关重要的环节。近年来,针对这一热点难点问题,国内外众多专家学者提出了多种解决方法。主要包括: 傅里叶变换法、 导数法[2-3]、 小波变换法[4-5]、 等等。但是傅里叶变换法实际操作中难度过大,导数法对信噪比要求很高,小波基的选择对小波变换法起至关重要的作用且重叠峰分离度较低时分峰误差过大。二次微分与近似对称的紧支集正交系列小波变换处理色谱的重叠峰由林兆培[6]等提出,但没有对分离度低于于0.4的重叠峰进行分解且没有进行误差分析。罗海军[7]等提出峰锐化法,但易造成峰型失真。传统使用的离散小波处理低分离度重叠峰会造成混叠现象[8]。而四次导对比二次微分能有效的提高分离度和去除杂峰,结合三样条小波变换法可以更准确的分离重叠峰。当X射线能量与元素接近时,会出现X荧光光谱严重重叠甚至完全重叠的情况[9]。对于低分离度重叠峰难以分离的重点热点问题,本文提出四次导数结合三样条小波变换的新方法处理这一问题。
1 原 理
1.1 导数法
导数的定义: 假设一个离散信号为X={x1,x2, …,xn}, 那么它的导数谱可以表示为
(1)
式(1)中,n为导数阶数,n≥1;h为步长。导数谱有如下性质;
(1)原始信号的极值点为偶数阶导数谱的极值与奇数阶导数谱的零点。
(2)原始信号的形变点为偶数阶导数谱的零点与奇数阶导数谱的极值点。
(3)原始信号形状会随着导数阶数的增加造成峰宽窄小、 峰型尖锐等现象。
有文献表明,四阶导数法能有效去除谱中的细小杂峰,可将重叠的特征峰分离,四阶导数对重叠峰的分辨效果相较于一阶和二阶导具有更优秀的效果[10]。导数谱应用于X荧光光谱特征峰的解析理论已经十分成熟。由导数性质可知,经导数处理之后的信号极值点以及零点均能表现出来,且使峰型尖锐,实现重叠峰初步分离。但随着导数阶数越高噪声也随之放大,实际使用中效果并不理想,所以急需一种方法让导数发挥作用。
1.2 三样条小波变换理论
对重叠峰处理的结果会随着选用的样条小波基的不同而发生变化。经二阶样条小波处理后的峰型表现为锯齿状,而四阶样条小波处理后会对峰位造成较大误差[11]。相较于二阶、 四阶样条小波,三阶样条小波分解具有特征峰面积误差较小、 特征峰位置基本不变的优点[12]。所以选用三阶样条小波基。
(1)样条小波的性质和定义
利用小波变换对EDXRF光谱分析的基本思路为: 首先选择适当的父函数和母函数,然后将原始信号进行离散小波变换,得到不同尺度上的信息,其中高频部分代表能谱峰信号,最后对高频信号进行乘以一个加权系数而将其进行分解。
设m为自然数,则定义m阶B样条Nm(x)如下
(2)


(3)
B样条小波可以通过递推得到,首先,取N1(x)为Haar尺度函数,然后通过Nm-1(x)和N1(x)作卷积来定义Nm(x)。如果将式(2)中取
(4)

图1和图2中的高通与低通滤波器系数取自三阶样条小波bior3.5。

图1 分解低通滤波器与高通滤波器系数Fig.1 Decompose low pass filter and high pass filter coefficients
(2)以下为四阶导数法结合三阶B样条小波算法实现步骤:
第1步,对待测信号进行四次导数初步处理,提高重叠峰分离度;
第2步,对处理后信号进行多分辨分析,找出最佳的重叠峰高频细节信号;
第3步,取一个加权因子对得到的高频细节信号进行一定的放大;
第4步,通过重构低通与高通滤波器系数对多分辨分析后的离散信号进行重构,最终得到分离之后的重叠峰。
1.3 四次导结合三样条小波变换分解低分离度重叠峰
式(5)中R为描述相邻两峰之间重叠度的一个指标[13],

图2 重构低通滤波器与高通滤波器系数Fig.2 Reconstructed low pass filter and high pass filter coefficients
其定义为
(5)
R趋近于0则表明重叠峰重叠程度越高。
在实验建模中,通常模拟重叠峰的函数分别是Lorentzian峰信号、 Gaussian峰信号[14]以及Tsallis峰信号[15]。
Gaussian峰信号
f(x)=Ae|-(x-μ)2/(2δ)2|
(6)
Lorentzian峰信号
f(x)=Aσ2/[(x-μ)2+σ2]
(7)
Tsallis峰信号
(8)
式(6)—式(8)中,σ是峰的宽度,A为峰值,μ是峰的顶点位置。而Gaussian峰和Lorentzian峰可以通过Tsallis峰调节q得到。当q接近1为Gaussian峰,q=2的时候为Lorentzian峰。综上所述,采用Tsallis峰函数进行模拟更具有说服力。
取q=1.8,同时取A的值分别为2, 1.5, 1.5。σ分别取4,2,1。μ分别取20, 24, 28。即峰位为20, 24, 28。而峰1和峰2的R1为0.33,峰2和峰3的R2为0.67。图3可以看出第1个峰与第2个峰严重重叠,第2个峰与第3个峰部分重叠,模拟信号更接近实测信号。

图3 模拟信号重叠峰Fig.3 Analog signal overlap peak
进行四阶导初步处理后能清楚的辨别峰位以及峰数量,所以利用四阶导进行初步处理是可行的,但是经过初步处理之后模拟信号存在部分重叠,因此需要结合另一种方法进行进一步的处理。

图4 四次导初步处理模拟信号Fig.4 The fourth derivative processes the signal
通过对模拟信号进行四阶导初步处理再进行三样条小波处理,模拟信号峰的峰位为20, 24, 28。处理后的峰位为19.9,24.2和27.8,峰位的误差分别为0.05%,0.83%以及0.71%。处理后的特征峰峰位误差较小,满足进行定量定性分析要求。模拟实验结果证明四次导结合三样条小波变换可以有效分解低分离度重叠峰。

图5 重叠峰分解模拟结果Fig.5 Overlapping peak decomposition results

表1 峰位结果分析Table 1 Peak position analysis
2 实验部分
从X射线能量表可知: K元素的KαKβ分别为3.313和3.589 keV, 能量仅差0.279 keV; 在实测K元素的过程中,由于能量差过小,会导致特征峰产生严重重叠。已知一组K系谱线不重叠的光谱,识别其能量峰道址为标准能量峰道址,用E=0.030 7 keV·ch-1进行能量线性刻度。K元素的KαKβ能量道址分别为113和122。用式(8)进行模拟EDXRF光谱中的低分离度重叠峰。KαKβ能量峰的比值为5∶1。模拟表达式如式(9)所示,结果如图6所示。

图6 重叠峰分解仿真结果Fig.6 Overlapping peak decomposition results
(9)
如图6所示,模拟EDXRF光谱的重叠峰得到了分解,且图6中的原始谱线中的重叠峰几乎完全重叠。使用寻峰法获得分解后的峰位,结果如表2所示,仿真K元素的重叠峰分解后的峰位结果误差小于1%。结果表明,四次导结合三样条小波变换能较好的分解EDXRF光谱中的重叠峰。
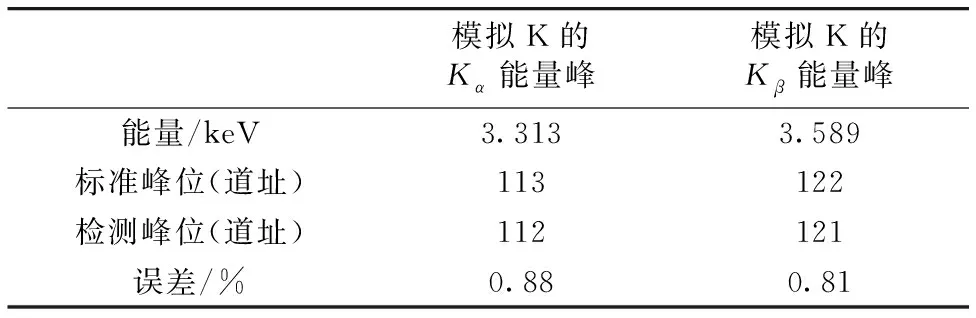
表2 峰位结果分析Table 2 Peak position analysis
3 结果与讨论
在本实验中采用的是CIT-3000SY X荧光元素录井仪实测的T铅黄铜元素数据以及混合轻元素数据,在T铅黄铜数据中在道址400~430之间Ni的Kα以及Co的Kβ能量分别为7.477和7.649 keV,仅相差0.172 keV,处于严重重叠状态。而在轻元素数据中,可以观察到在道址230~270之间的Cr和Mn元素存在严重重叠,能量相差0.484 keV,对元素辨别造成较大困难。本组对这两组数据已经进行过谱光滑本底扣除等预处理,然后进行四阶微分结合三样条小波分解,其中使用4层的小波分解以及6倍的高频细节信号方法系数。分解结果如图7和图8所示。

图7 实测T铅黄铜元素EDXRF光谱重叠峰分解结果Fig.7 Decomposed results of measured T Leaded brass X-ray fluorescence spectrum
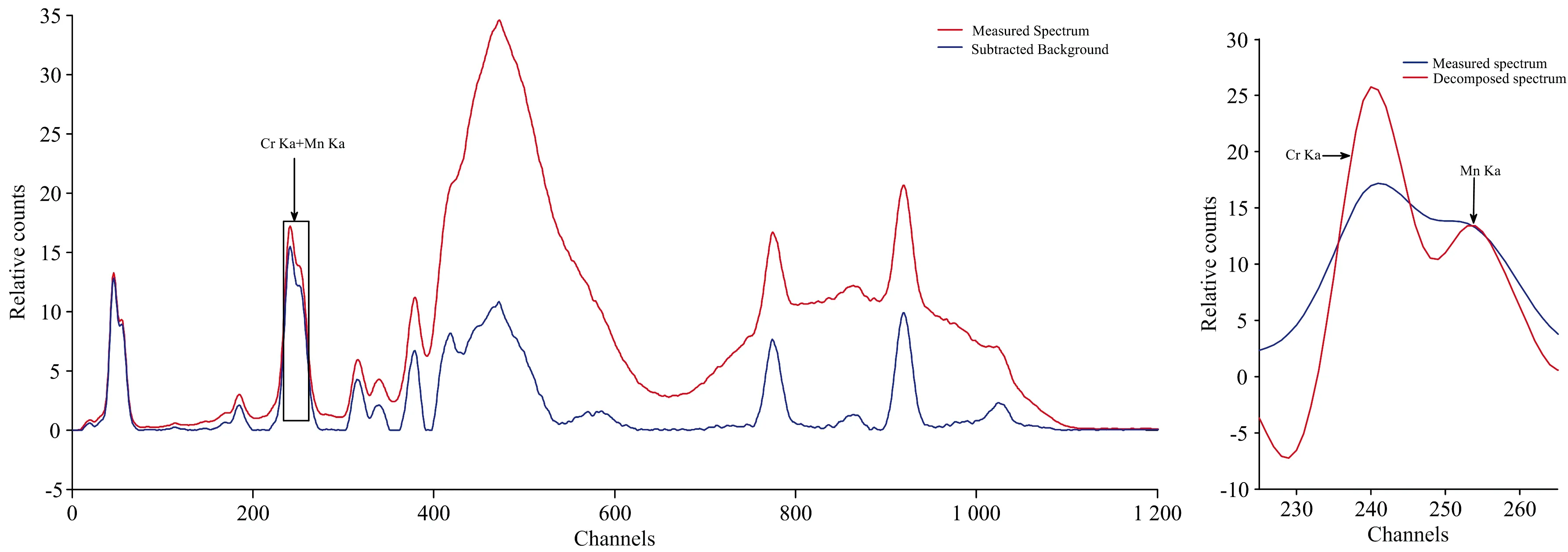
图8 实测轻元素EDXRF光谱与分解结果Fig.8 X-ray Fluorescence spectrum of light element and Overlapping peak decomposition results
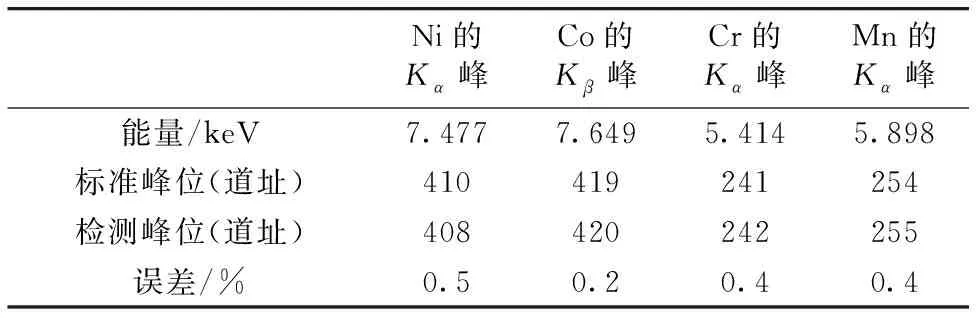
表3 峰位值结果分析Table 3 Peak position analysis
已知Ni的Kα标准峰位道址为410,Co的Kβ的道址为419,用寻峰法识别分解后的光谱峰位道址为408和420,误差仅为0.5%,0.2%,Cr标准峰位道址为241,Mn的标准峰位道址为254,分解后的误差仅为0.4%。且重叠峰分解效果明显,结果表明: 四阶导数结合三样条小波分解实际X荧光谱中分离度较低的重叠峰具有精确的结果。
4 结 论
本文分别研究了导数法以及样条小波变换法的基本原理,结合两种方法的优点提出了四阶导数结合三样条小波变换处理低分离度重叠峰的新方法。通过模拟实验证明可以有效的分解重叠峰。然后,用此方法处理了仿真能量色散X荧光光谱以及实测EDXRF光谱,都实现了重叠峰的分解且误差较小,可以实现元素的辨别。结果证明: 此方法能有效的分解分离度较低的重叠峰,且在解决EDXRF光谱的重叠峰现象具有实用性。

