基于随机秘钥蝙蝠算法的多行设施布局设计
董舒豪 徐志刚 秦开仲 常艳茹 苏开远 朱建峰
1.山东大学机械工程学院,济南,2500612.山东大学深圳研究院,深圳,518057
0 引言
设施布局问题是指在给定的空间与约束条件下,将生产系统的各种资源进行合理的组织与分配,以使设计目标集达到最优[1]。设施布局对制造企业的物料搬运、在制品库存、交货期、生产效率、工作空间、环境等方面均具有重要的影响,关系到企业能否高效率、低成本运营[2-3]。
多行设施布局作为一种常见的设施布局形式,具有节约生产空间、物料传输柔性高、搬运设备利用率与容错能力高的优点,适用于零部件种类多、工艺复杂的情况[4]。多行设施布局形式的生产系统中通常分布有横向与纵向交错的通道,横向通道两边的行中分布有设施,纵向通道分布于行内,横纵交错的通道可以保证搬运设备沿着通道在同一行、行与行的设施之间合理地进行物料搬运,因此通道数量和位置的设计直接关系到多行设施布局方案的有效性。但目前诸多研究中,通常较少考虑通道对多行设施布局中物料搬运的影响,而是以欧氏距离(直线距离)或曼哈顿距离(矩形距离)表示设施间物料搬运的距离,这就可能造成最终的布局方案不能满足设计要求[5]。LEE等[6]和PAUL等[7]分析了考虑通道的多行设施布局问题中搬运距离的计算方法,但其中通道的位置和数量均为固定。本文第一作者等[5]研究了考虑行内纵向通道位置不确定情况下的多行设施布局,但假定行内纵向通道的数量为已知。行内纵向通道数量和位置均为不确定的多行设施布局问题的研究还未见报道。例如,在实际多行设施布局形式的车间中,通常需要在中间行内设计一定数量、合理位置的纵向通道,使搬运设备在各行之间合理地执行物料搬运任务,若纵向通道的数量太少或位置不合理,则可能导致车间内物料搬运的距离增加;若纵向通道数量过多,则可能会导致布局空间不足,因此,在设计过程中需要对车间内纵向通道的数量、位置进行综合考量。
多行设施布局问题属于NP-hard问题,故智能优化算法成为求解该问题的常用手段[8],如遗传算法(genetic algorithm, GA)[2,6]、粒子群优化(particle swarm optimization, PSO)算法[1,7]、蛙跳算法[9]、模拟退火算法[8,10]、蚁群算法[8]、萤火虫算法[11]等。YANG[12]提出的蝙蝠算法(bat algorithm, BA)融合了GA算法、PSO算法与和声搜索算法的优点,最初是针对连续性优化问题而开发的,并在连续性优化问题测试中展现出较好的性能。LATIFI等[13]将BA算法[12]应用于具有连续性质的开放式设施布局问题中,以设施横纵坐标进行编码。此外,很少有离散性质的设施布局问题(如单行设施布局、多行设施布局等)运用BA算法,原因是BA算法中的频率、速度、位置等更新公式均是为连续性问题而设计的[14]。在其他离散问题领域的研究中,通常摒弃了BA算法中的频率、速度、位置等连续型更新公式,而采用其他离散型的更新算子,如2-exchange算子[15]、交叉算子[14,16]、交换和插入算子[14,17]、2-opt算子[15,17]等,这样处理并未较好地遵循BA算法本身的思想,且在离散化过程中会提高算法的复杂性[18]。为了发挥BA算法在求解连续性优化问题中的优势,克服其在多行设施布局问题中应用的难点,在不引入离散型更新算子的前提下,可以借鉴KANG等[18]的研究成果:将随机秘钥(浮点数)编码的思想应用于布谷鸟搜索算法(cuckoo search, CS)中,解决同是离散性质的闭环设施布局问题,该方法通过随机秘钥在连续空间上的更新映射为布局解的变化,使CS算法中的莱维飞行得以实现。
本文综合考虑多行设施布局问题中行内纵向通道数量和位置均为不确定的情况,建立该问题的数学模型。鉴于BA算法在连续性优化问题中表现出的优势,本文采用BA算法进行模型求解,为了使其得以应用于离散性质的多行设施布局问题中,采用随机秘钥编码思想,提出一种基于映射规则的随机秘钥蝙蝠算法(random-key bat algorithm, RKBA),通过定义算法中蝙蝠位置向设施布局组合解的映射规则和映射步骤,使算法能够在连续空间上执行,并在离散空间上映射出码长不同的解(布局方案),以实现BA算法在多行设施布局问题中的应用,从而设计出切实有效的布局方案。
1 问题的描述与建模
1.1 问题描述
本文所研究的多行设施布局形式如图1所示,具体描述如下:从布局区域的左侧边界开始,将一系列宽度相等、长度不等的矩形作业单元分配到若干个具有相同高度(即作业单元的宽度)的行中,行与行之间分布有横向通道,中间行内分布有纵向通道,以使设计目标集达到最优。该提布局方式常见于餐厅、工位较多的办公室、行与直线通道整齐排布的车间等场景中,本文以车间作为研究对象。图1中,wh表示横向通道的宽度,wv表示纵向通道的宽度,wf表示行的高度,即每个作业单元的宽度。
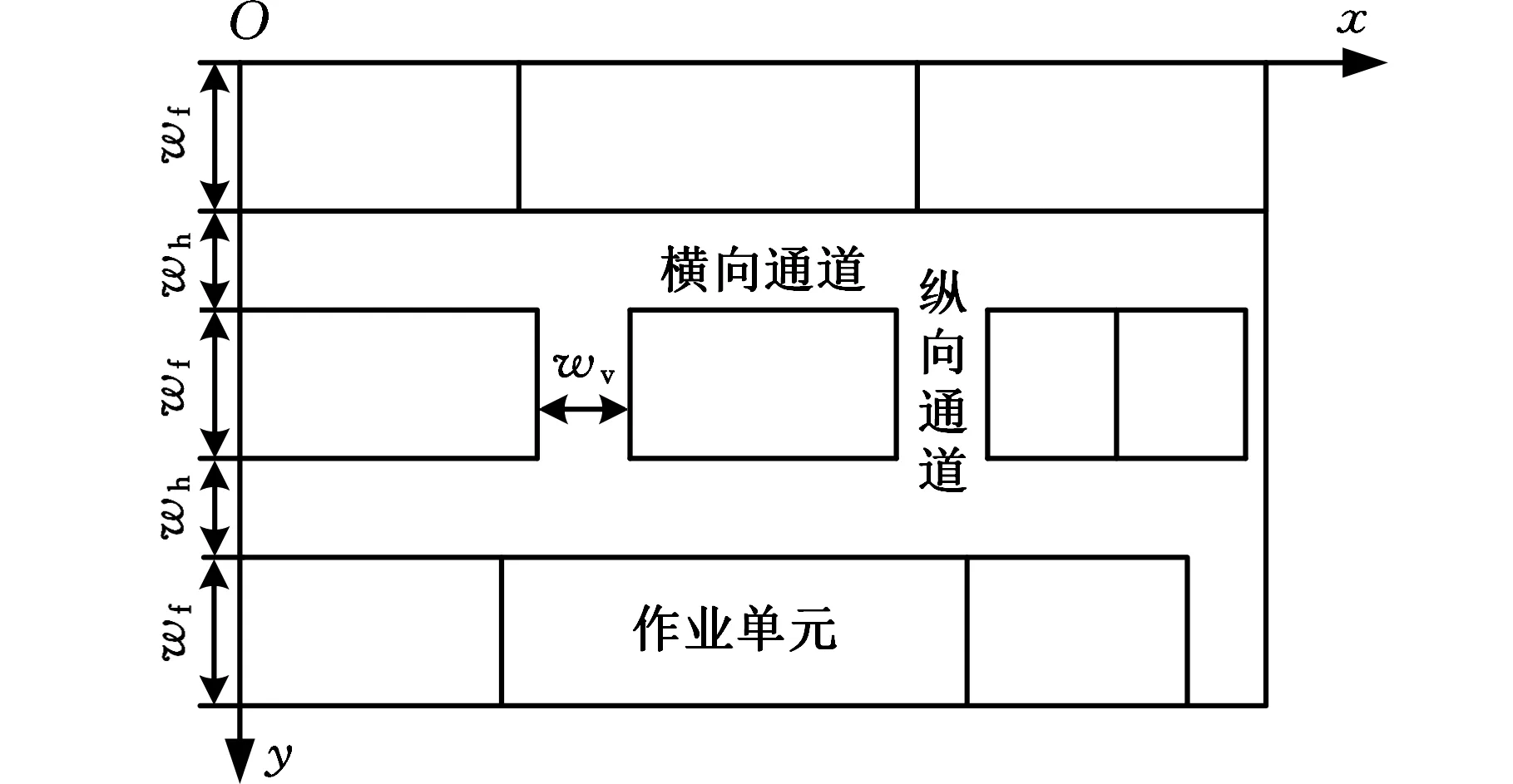
图1 多行设施布局的形式
本文所研究的多行设施布局问题还有以下前提条件:①每个作业单元的长和宽均为已知的固定值;②作业单元的物料搬运点均位于其中心点;③所有作业单元与通道所占面积之和小于矩形布局区域的总面积;④横向通道与纵向通道的宽度已知,横向通道的数量已知、位置已定,纵向通道位于中间行内,每一中间行内纵向通道的数量和位置均不确定。
1.2 多目标函数
1.2.1最小化物流强度
最小化物流强度即要求作业单元间物流量与物料搬运距离乘积之和最小,目标函数如下:
(1)
其中,n为作业单元的数量;fij为作业单元i至作业单元j的物流量;dij为搬运设备沿通道从作业单元i向作业单元j行进的距离。为准确求得其值,归纳出多行设施布局中物料搬运的基本类型,如图2所示。

(a)同行搬运 (b)邻行搬运
图2a中,同行搬运的距离计算公式为
dij=|xi-xj|+|yi-y′|+|yj-y′|
(2)
其中,xi、yi分别为作业单元i中心点的横坐标、纵坐标;y′为作业单元i和j临近的同一横向通道y方向上的中心坐标。图2b中,临行搬运的距离即为曼哈顿距离:
dij=|xi-xj|+|yi-yj|
(3)

(4)
则可以确定图2c和图2d所需绘制的节点数量分别为4和7。以图2d为例,节点①和⑦为两作业单元i和j的中心点,节点②和③为第二行中纵向通道的中心点,节点④、⑤和⑥为第三行中纵向通道的中心点,进而可以生成图3所示的邻接图与邻接矩阵。邻接图上具有可达关系的节点之间的距离即为节点之间的曼哈顿距离,无可达关系的节点之间的距离记为∞。

图3 邻接图与邻接矩阵
对于上述跨行搬运,在所生成的邻接图和邻接矩阵的基础上,本文采用Dijkstra算法求解两作业单元间物料搬运的最短搬运距离dij,其具体求解步骤见文献[5]。
1.2.2最小化搬运设备空载运行强度
搬运设备的空载运行与前述物料搬运是相互独立的,以图4说明搬运设备的空载运行。当作业单元i到作业单元j有物料搬运请求时,搬运设备可能停靠在某一不确定的作业单元l处,接到搬运任务后空载运行至作业单元i;或者搬运设备正在搬运作业单元k至作业单元l的物料,搬运完成后再由作业单元l空载出发至作业单元i,然后才能完成作业单元i到作业单元j的物料搬运。
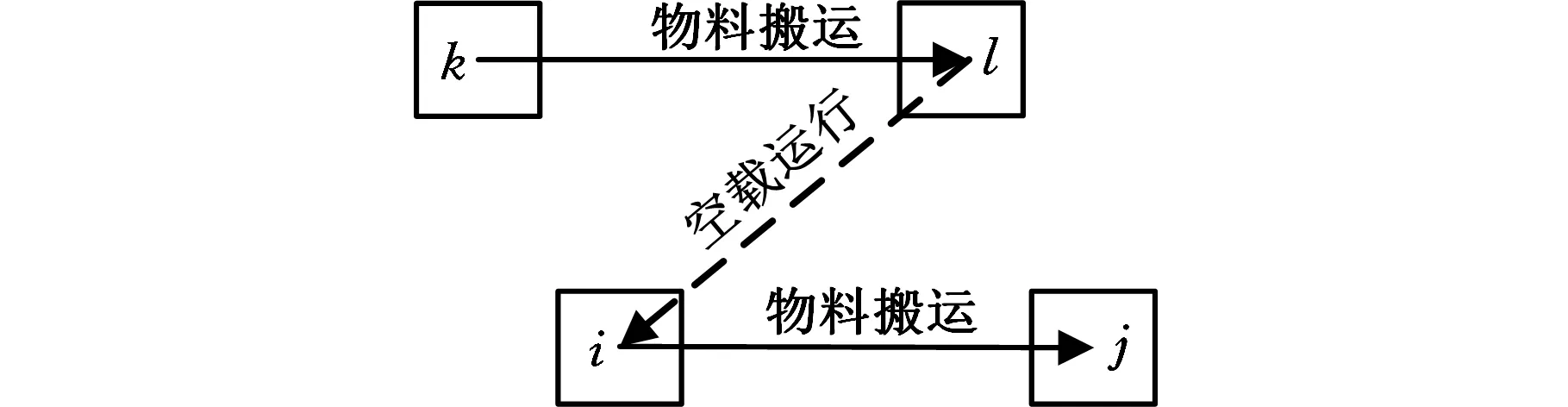
图4 搬运设备的空载运行
考虑到各种工件在不同工序的加工批量、加工时间具有不确定性,所以搬运设备的位置状态也可能具有不确定性。设搬运设备为完成作业单元i到作业单元j的物料搬运而需从某一不确定作业单元l处空载出发至作业单元i的概率为Pl,根据文献[19],Pl可表示为
(5)
由式(5)可知,当其他作业单元至作业单元l有较大的物流量时,搬运设备从作业单元l处空载出发的概率就较大。进而,搬运设备为完成作业单元i至作业单元j的物料搬运所需要空载运行距离的期望值可表示为
(6)
综上,搬运设备空载运行强度的目标函数可表示为
(7)
式中,c为物料搬运设备的空载系数,即物料搬运设备空载运行时与载有物料运行时单位距离运行成本的比率,本文取其为油耗比。
1.2.3最大化相互关系
作业单元之间的相互关系通常与搬运距离无关,而与作业单元之间的欧氏距离有关,其目标函数可以表示为
(8)

1.3 数学模型
对式(1)、式(7)和式(8)中的fij和rij进行标准化处理[20],消除量纲差异:
(9)
(10)
引入权重系数w1、w2、w3,将多目标函数转化为单目标函数,构建以下数学模型(约束条件为中间行中纵向通道的数量约束,其余约束条件详见文献[5],也可通过扫描本文篇首处OSID码获得):
(11)
其中,nk为第k行中的纵向通道数量,nkmax和nkmin分别表示第k行中纵向通道数量的最大值和最小值。
2 随机秘钥蝙蝠算法设计

2.1 蝙蝠速度和位置的随机秘钥编码

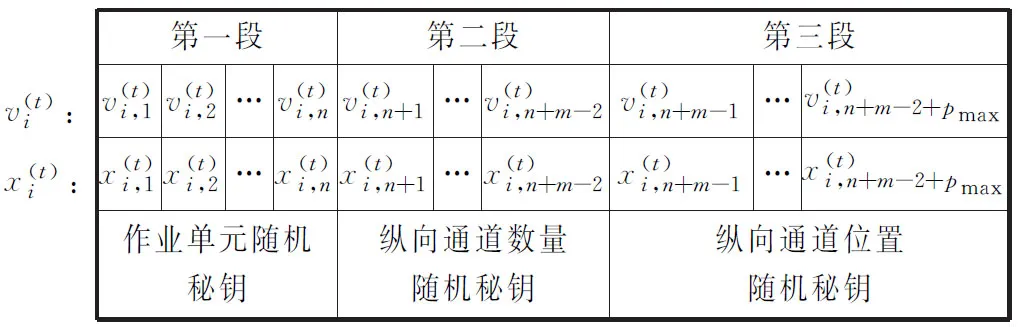
图5 蝙蝠速度与位置的随机秘钥编码
2.2 蝙蝠位置向布局解的映射
蝙蝠位置用随机秘钥(浮点数)组成的随机秘钥串表示,而多行设施布局的解通常表示为整数码串,因此,需要建立蝙蝠位置与布局解之间的映射关系。本文将蝙蝠位置向解的映射分为以下三步:①作业单元与纵向通道数量随机秘钥的映射;②边界约束的修正;③纵向通道位置随机秘钥的映射。假设有10个作业单元需要布置在四行内,中间两行内纵向通道的数量要求为n2max=n3max=2,n2min=n3min=1,该布局中蝙蝠位置向多行设施布局组合解映射过程的一个实例见图6,该映射方法根据蝙蝠位置的不同,可能得出不同长度的解。
2.2.1作业单元与纵向通道数量随机秘钥的映射
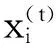

(a)作业单元与纵向通道数量随机秘钥的映射
(12)
∂,k,κ∈Nk∈[2,m-1]

2.2.2边界约束的修正

(1)判断第m行中是否存在某一作业单元的长度小于lmax,若是,则执行步骤(3),否则执行步骤(2)。
(2)随机产生一个新的蝙蝠位置,替代当前蝙蝠位置,并执行2.2.1节的映射操作,然后判断是否满足边界约束,若是,则跳出修正操作,否则执行步骤(1)。
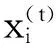
(13)
式中,rrand∈(0,1)。
(4)若最后一行中的作业单元总长度小于或等于布局区域的总长度L,则跳出修正操作,否则继续执行步骤(1),直到满足布局边界约束为止。
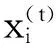
2.2.3纵向通道位置随机秘钥的映射

(14)
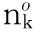

2.3 全局搜索

(15)
(16)
(17)
式中,fmin、fmax分别为蝙蝠频率的最小值和最大值;β为[0,1]上的随机数;x*为当前种群中的最优蝙蝠位置。

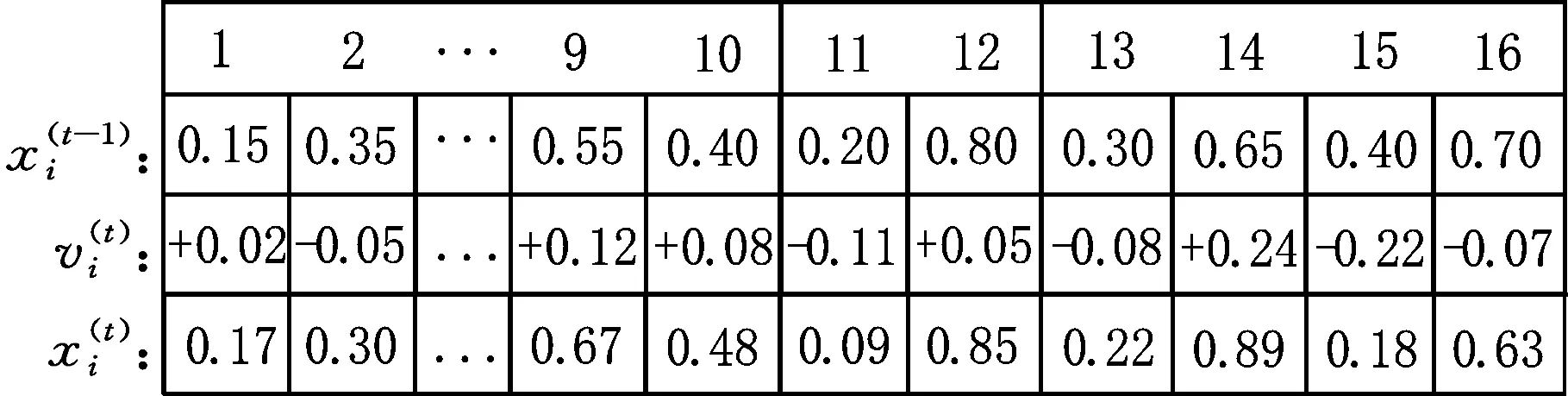
图7 蝙蝠位置的全局更新
2.4 局部搜索
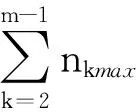
x′*=x*+εA(t)
(18)



图8 蝙蝠位置的局部更新
2.5 音量和脉冲发生率的更新
(19)
(20)

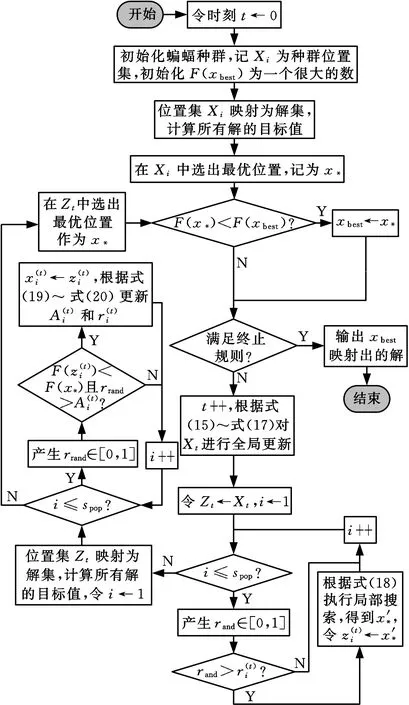
2.6 本文所提RKBA算法的执行流程
对于本文所需求解的最小化问题,设xbest为历史最优位置,记F(x)为蝙蝠位置x所映射出的解的目标函数值,则本文所提RKBA算法的流程如下:

(2)完成Xt到解的映射,计算Xt所映射出的解集的目标值,选出Xt中的最优位置,记为x*。
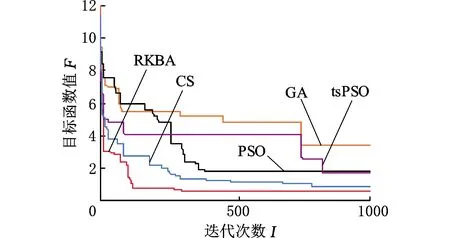
(3)将x*与历史最优位置xbest进行对比,若F(x*) (4)如果满足算法终止规则,则输出xbest所映射出的解,否则继续执行下一步。 (5)t+ +,根据式(15)~式(17)对Xt中的蝙蝠位置进行全局更新。 (8)选出Zt中的最优位置作为x*,并继续执行步骤(3)。 以上步骤(6)引入Zt代替Xt执行局部搜索的目的是避免步骤(7)执行过程中遗失潜在的全局最优蝙蝠位置。本文所提RKBA的执行流程如图9所示。 图9 本文所提RKBA的流程图 以国内某农机设备的生产车间为实例,该车间长64 m,宽41 m,现有18个作业单元拟分配到车间内的四行空置区域中,行的宽度与作业单元的宽度均为8 m,横向通道与纵向通道的宽度均为3 m,其中中间两行内要求具有1~2条纵向通道,即n2max=n3max=2,n2min=n3min=1,使得物料搬运顺利进行。作业单元的长度信息见表1。 表1 作业单元长度 作业单元之间的物流量与相互关系见表2和表3,其中未列出的作业单元之间的物流量和相互关系为0。此外,表2中作业单元之间区分从至关系,即当作业单元i和j之间物流量不为0时,通常有fij≠fji(i≠j);表3中作业单元之间不区分从至关系,即rij=rji(i≠j)。 表2 作业单元间物流量 表3 作业单元间相互关系 图10 各算法最优结果的进化曲线 从图10可以看出,相对于其他几种算法,本文所提出的RKBA算法具有更快的收敛速度,且所得解的质量更高。所有测试结果中目标函数最优值为RKBA算法得到的0.5325,对应的布局解与布局方案如图11所示。 图11 最优解及其对应布局方案 记录5种算法分别独立测试20次后最优目标值的最佳值、最差值、平均值及算法的平均运行时间,各性能指标的对比见表4。此外,记录5种算法分别独立测试20次的平均最优目标值进化曲线,如图12所示。 表4 算法性能的对比 图12 各算法平均最优目标值进化曲线 根据表4与图12的测试结果,对算法进行对比分析。首先可以看出GA算法的寻优效果较差,原因可能是GA算法的局部寻优能力较差,虽然种群多样性较好,但局部搜索能力弱、搜索深度不够,导致其出现“早熟”。PSO和tsPSO两种算法在整体寻优质量上相差不大,但tsPSO算法比PSO算法的运行时间略短,也说明tsPSO算法较PSO算法具有一些优势,但对比CS算法与RKBA算法,PSO算法和tsPSO算法的求解质量相对较差,原因可能是:虽然PSO算法、tsPSO算法采用惯性权重来平衡全局搜索和局部搜索,但它们在搜索过程中没有围绕种群最优粒子位置进行小步长的局部搜索,导致它们的搜索结果不理想,而CS算法中的“抛弃”操作与RKBA算法中的局部搜索均是围绕种群最优个体执行的小步长深度搜索,所以具有较好的寻优效果。CS算法的求解质量较高,也说明该算法中的莱维飞行具有较好的寻优效果,使算法具有较好的局部深度搜索能力,但CS算法的搜索时间比其他几种算法都要长。RKBA算法在求解质量、寻优时间、收敛速度上均表现出了较好的性能,从求解质量来看,RKBA算法的求解质量远高于GA算法、PSO算法与tsPSO算法的求解质量,相对于CS算法也具有一定的优势;从寻优时间来看,RKBA算法的求解时间最短,且远远领先于CS算法;从收敛速度来看,相对于GA算法、PSO算法与tsPSO算法,RKBA算法的收敛速度明显更快,与CS算法相比,在迭代前期,RKBA算法与CS算法均具有较快的收敛速度,但在搜索至约200代之后,RKBA算法的收敛性能要优于CS算法。综上所述,RKBA算法在求解本文多行设施布局问题中具有较好的寻优效果,可以更加快速、高效地生成可行的多行设施布局方案。 (1)本文建立了行内纵向通道数量和位置具有不确定性的多行设施布局优化模型。该模型以最小化物流强度、最小化搬运设备空载运行强度和最大化作业单元相互关系作为设计目标,并给出了搬运设备沿通道进行物料搬运的距离计算方法。 (2)提出了一种基于映射规则的随机秘钥蝙蝠算法。在不引入其他离散型更新算子的前提下,将蝙蝠算法中的蝙蝠速度和位置用随机秘钥表示,根据所建立的多行设施布局优化模型定义了蝙蝠位置向解的映射规则和映射步骤,使算法可以在连续空间上执行,并在组合空间上映射出码长不同的布局方案。映射方法的建立使所提出算法既能发挥蝙蝠算法在求解连续性优化问题中的优势,又能解决本文所研究的离散性质的设施布局问题。通过一个实例,将随机秘钥蝙蝠算法与其他算法进行了求解对比,生成了有效的多行设施布局方案,并证明了所提出算法的有效性。 设施布局是一类复杂的实际问题,目前该领域仍存在许多实际因素未被深入挖掘。今后可考虑设计过程中的实际因素,如物料装卸点问题、障碍物问题(墙壁、立柱、固定设备等),使问题更符合实际,模型更加完善。

3 实例求解测试
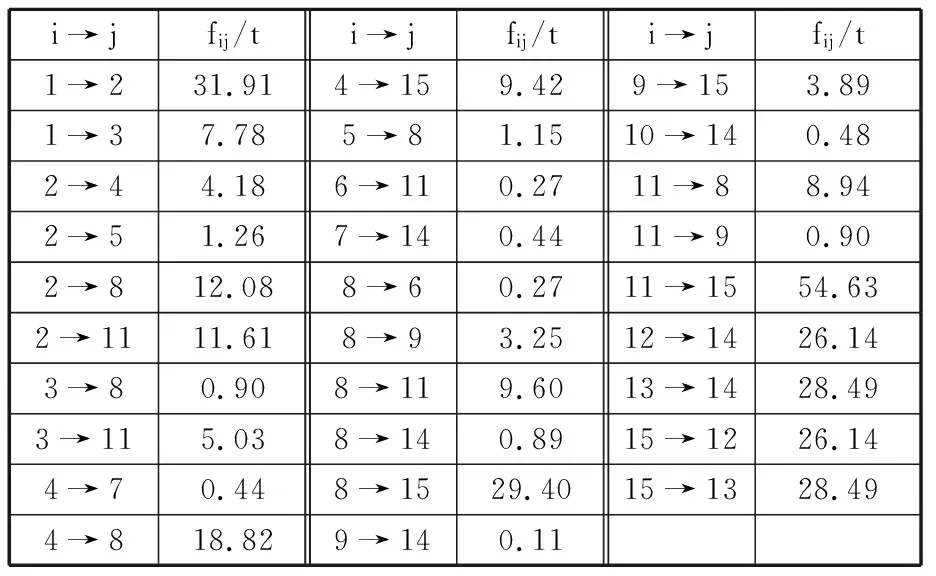
3.1 基础数据


3.2 实例求解与算法分析

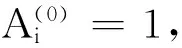



4 结论

