改进数字锁相细分方法的FPGA电路设计
任雪玉,朱维斌,黄 垚,薛 梓
(1.中国计量大学计量测试工程学院,浙江杭州 310018;2.浙江大学光学科学与工程学院现代光学仪器国家重点实验室,浙江杭州 310027;3.中国计量科学研究院,北京 100029)
0 引言
随着我国制造业的蓬勃发展,角度测量技术正朝着高分辨率、高精度、动态、实时性以及测量稳定性等需求的方向发展[1-2]。目前国内在角度计量中所用圆光栅的栅距在20″ 以上,但是其计量分辨率要求达到0.1″,甚至更高,光栅制造技术受加工工艺和加工成本的限制,无法满足高精度、高分辨的需求。因此采用莫尔条纹信号细分技术提高测量系统的分辨力和精度具有较好的实用价值[3]。
传统的电子细分方法包括幅值分割细分法、载波调制细分法、锁相倍频法等[4]。幅值分割细分法可以获得较高的细分数,但是电路较复杂,对幅值相关特性要求较高;载波调制细分法的精度较高,但是电路对信号的正交性要求较严格,同时电路的复杂度也较高。
锁相倍频细分法是对信号的相位进行细分,对原始信号质量要求不高,硬件电路简单,因此被广泛使用[5-7]。传统的数字锁相倍频细分法通过调节输入信号与反馈信号之间的相位差,使输出信号N分频之后的反馈信号频率自动跟踪输入信号的频率,从而完成输入信号频率的N倍细分功能。但是,传统的数字锁相细分方法采用闭环结构,在环路锁定之前需要较长的获取时间使环路达到锁定状态,才能对输入信号进行倍频,并且受数控振荡器的影响,输入信号频率变化范围较窄。因此传统的数字锁相细分方法不能实时得到输入信号细分的结果,不能够满足于动态角度实时测量要求。
因此本文提出一种改进数字锁相细分方法,分析改进锁相细分方法的原理及电路系统设计,并且详细分析和仿真验证了该方法中小数分频各个模块电路系统设计。在FPGA平台上实现不同动态工况下,传感器输出信号的实时128倍细分,显著提高了动态测量分辨率,为提高超精密机械加工技术奠定了基础。
1 改进数字锁相细分原理
改进数字锁相细分方法采用开环结构,主要由边沿检测器、时间数字转换器、小数分频算法、频率控制字调节算法和分频器构成,如图1所示。

图1 改进数字锁相细分原理图
边沿检测器判断输入信号x(n)的周期起始时刻,时间数字转换器利用系统高频时钟fclk对x(n)的周期进行量化,量化值为
(1)
式中:int(·)为向下取整函数;fi为输入信号的频率。
根据输入的量化值Q和细分倍率N,计算出时钟分频因子为
(2)
随着输入信号频率的改变,当Q和N为整数时,时钟分频因子C可能为小数,但是FPGA数字电路无法实现小数分频,因此设计小数分频方法,该方法利用整数频率控制字的相互组合实现小数分频。其中包括小数分频算法、频率控制字调节算法和分频器。
小数分频算法根据量化值Q和细分倍率N,能够确定与输入信号频率相对应的整数频率控制字M为
(3)
与M和M+1对应的频率为
(4)
fM和fM+1对应的周期个数为k1、k2,为实现N倍细分任务,令k1+k2=N,在输入信号x(n)的一个周期Ti内,输出k1个频率为fM的信号和k2个频率为fM+!的信号,即:
Ti=k1TM+k2TM+1
(5)
式中:TM=1/fM;TM+1=1/fM+1。
把式(6)~式(10)代入式(11),化简得:
k1M+k2(M+1)=Q
(6)
式(6)中,所有变量均为整数,小数分频算法仅得到M、M+1、k1、k2的取值,频率控制字调节算法调节N个整数频率控制字输出的先后顺序。
频率控制字调节算法通过比较k1、k2的大小,将一个周期内的N个频率控制字分为A组,每组输出l个控制字数。频率控制字调节算法流程如图2所示。

图2 频率控制字调节算法流程图
以k1>k2为例,频率控制字调节算法将频率控制字分为了A=k2组,每组按顺序输出1个M+1和l-1个M,从而保证Ti时间内输出N个整数频率控制字。
分频器通过高频时钟频率fclk对整数频率控制字进行分频,即可以完成任意频率输入信号的N倍细分。
因此,改进数字锁相细分方法不仅可以实时对光栅传感器输出信号进行细分,提高测量分辨率,而且所有变量均为整数,确保可以在FPGA平台上施加改进数字锁相细分算法。
2 细分电路原理与结构
FPGA具有可并行、可重构、可定制等优点,可以承载改进锁相倍频细分任务。在电路系统中,需要实现信号量化值获取与小数分频两部分。电路系统原理图如图3所示。

图3 电路系统原理图
由图3可知,电路系统中量化值获取包括边沿检测和时间数字转换器两部分。边沿检测通过高频时钟检测输入信号上升沿,产生一个高电平EN触发时间数字转换器,利用系统时钟量化输入信号时间间隔,得到量化值Q。小数分频部分包括参数求解、频率控制字调节、分频器3个部分。
2.1 参数求解模块
参数求解模块主要由频率控制字的求解模块和控制字分组求解模块组成。图4为参数求解模块的RTL级仿真电路图。频率控制字的求解模块是根据量化值和式(12),利用乘法器和加法器完成对参数M、M+1、k1、k2的求解;控制字分组求解模块利用比较器和除法器完成对参数A、l的求解,输出全部参数M、M+1、k1、k2、A、l以及标志位update。
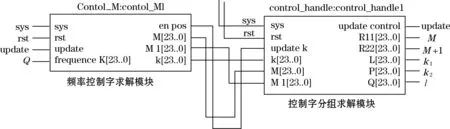
图4 参数求解电路的RTL级仿真电路图
参数求解模块的波形图如图5所示,当输入信号为变频方波时,实时更新参数计算结果,并产生一个计算结束标志位update。

图5 参数求解模块的波形图
2.2 频率控制字调节模块
频率控制字调节模块根据参数M、M+1、k1、k2、A、l的计算结果,调节频率控制字M和M+1的输出的先后顺序,图6为频率控制字调节模块的RTL级仿真电路图。

图6 频率控制字调节模块的RTL级仿真电路图
本模块采用三段式状态机实现如图6所示的调节逻辑,状态机由initation、S01、S02和S11 4种状态组成,状态机工作模拟图如图7所示。

图7 状态机工作模拟图
初始状态设为initation状态,此时判断参数更新标志位update状态。当update为高电平时,状态机跳转到S01状态,此时输出1个频率控制字M或M+1,每输出1个频率控制字变量cnt和cnt_all累加计数,当满足cnt=1条件时,cnt=0,状态机跳转到S02状态,此时输出l-1个频率控制字M或M+1,每输出一个频率控制字变量cnt和cnt_all累加计数,当满足cnt=l-1条件时,cnt=0,状态机跳转到S01状态,此时一组频率控制字输出完成,如此循环。当cnt_all=A·l时,输出A组频率控制字,状态机跳转到S11状态,此时输出剩余的N-A·l个M或M+1,每输出一个频率控制字cnt_all累加计数1次,当cnt_all=N时,状态机跳转到initation状态,完成对N个频率控制字的调节。
以k1>k2为例,当update为高电平时,状态从initation跳转到S01,此时输出1个M+1,变量cnt开始计数;当cnt=1时,cnt=0,状态从S01跳转到S02,此时cnt开始计数,输出l-1个M;当cnt=l-1时,cnt=0,状态从S02跳转到S01。当cnt_all=A·l时,状态从S02跳转到S11,输出剩余的N-A·l个M+1;当cnt_all=N时,状态从S11跳转到initation。
频率控制字调节模块的波形图如图8所示,当输入信号为变频方波时,实时更新不同的参数,状态机state_c处于不同状态时,输出不同的频率控制字M_cur给分频器,分频器通过高频时钟分频,得到倍频后的输出信号。
图8 频率控制字调节模块的波形图
3 实验与数据分析
为验证改进锁相细分方法的有效性,在实验室自制FPGA电路上加载实际信号进行细分功能的验证,电路板如图9所示,电路中选用40 MSPS、16位的ADC芯片获取传感器输出信号,EP4CE115F29C7作为处理改进数字锁相细分算法加载芯片,IS42S16320B作为动态采集存储芯片。

图9 实验室自制FPGA电路板
3.1 细分功能验证
为降低信号噪声的影响,选用信号发生器RIGOL DG4162作为信号源,模拟3种匀速运动工况,输出占空比为50%、频率分别为1.0、10.0、80.0 kHz的方波信号,验证改进数字锁相细分方法的有效性。
在改进锁相细分算法中设定fclk=200 MHz,N=128,3种不同工况下,分别采样得到的fi和f0,使用MATLAB进行数据分析,得到输入信号周期内采样点数与细分倍率之间的关系,如图10所示。

(a)1.0 kHz细分结果

(b)10.0 kHz细分结果
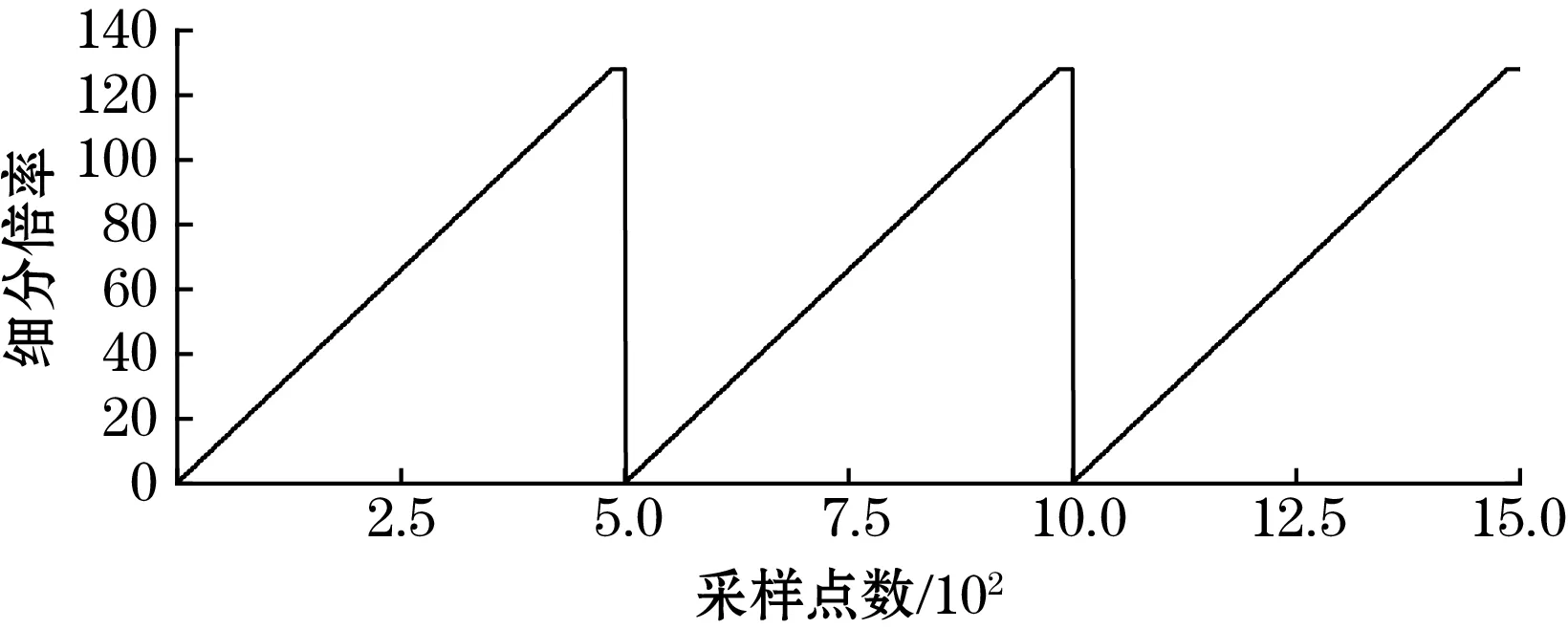
(c)80.0 kHz细分结果图10 3种不同频率信号的细分结果
由图10(a)、图10(b)可知,当输入信号为低频信号时,单周期内采样点数较多,因此不容易看出理论细分结果呈阶梯状线性增加,仅看出细分结果具有良好的线性度,且在随机抽取3个周期信号内信号细分数均为128。由图10(c)可知,当fi=80.0 kHz时,输入信号单周期内,采样点数较少,在输入信号单周期结束,采样点数为500、1 000、1 500左右时,明显看出细分结果的阶梯状。因此改进锁相倍频细分方法能够实现对光栅传感器输出信号的细分。
3.2 对比实验
选择传统的锁相倍频细分方法作为对比对象,在传统的锁相倍频细分算法中设置N=128,,在改进锁相细分算法中设定fclk=200 MHz,N=128,信号发生器分别输出频率为1.0、10.0、80.0 kHz的方波信号,在实验室自制FPGA电路上分别施加传统锁相倍频细分算法和改进的锁相倍频细分算法,实验得到3种不同工况下,参数如表1所示。
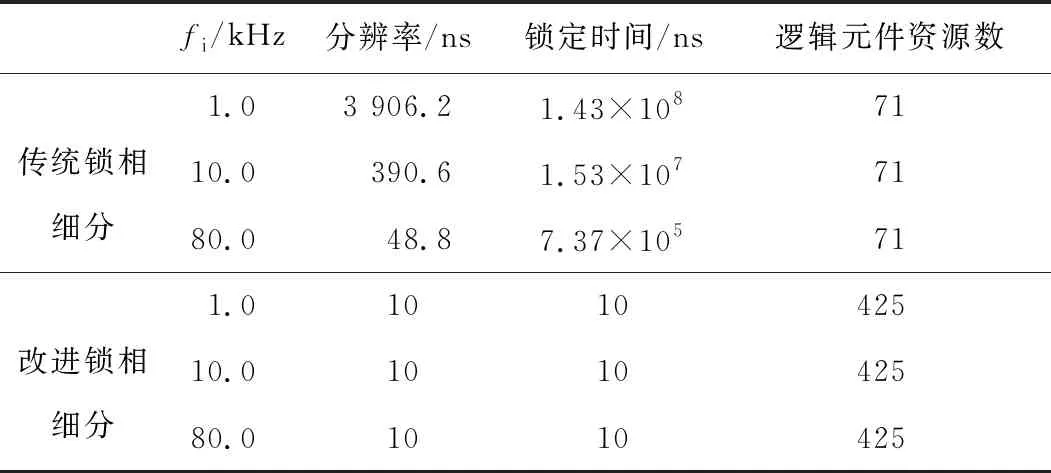
表1 传统锁相细分与改进锁相细分参数对比
由表1数据可见:
(1)改进锁相倍频细分方法的锁定时间不会随着输入信号频率的改变而改变。当输入信号频率为1 kHz时,改进锁相环仍能在10 ns内快速锁定,实时完成对输入信号的细分。
(2)改进锁相倍频细分方法的频率分辨率不会随输入信号频率的改变而改变,始终以10 ns的频率分辨率调节反馈系统,实现锁相细分。在硬件资源占用方面,芯片EP4CE115F29C7的逻辑元件总资源为114480,改进细分方法逻辑元件资源数虽然会增加,但是占用芯片整体逻辑元件资源百分比并没有很大改变。
4 结束语
本文对基于动态测量中光栅莫尔信号的细分技术进行研究,提出了一种改进数字锁相细分方法,开发了基于FPGA的改进数字锁相细分电路,完成了电路测试。在不同动态工况下,实现光栅传感器输出信号的128倍细分,且细分结果具有良好的线性度。通过对比实验,证明该方法不仅解决了传统数字锁相细分方法的不足,而且改进方法具有良好的动态特性以及较高的分辨率。

