改进随机惯性权重粒子群算法在灌溉配水中的应用

倪磊 罗英杰 苏正扬 李文翔 李晓钰

(成都工业学院网络与通信工程学院，四川 成都 610400)

引言

灌溉配水已成为当前节水农业的研究焦点，粒子群优化算法(PSO)是近年来广泛关注和研究的智能优化算法之一，该算法具有收敛速度快、鲁棒性好、通用性强，优化问题的过程简单等优点，但收敛速度慢，容易陷入局部最优解。多年来很多学者都对粒子群算法进行优化改进，郭丽丽等[1]提出的线性递减动态惯性权重(LDW)存在着早熟收敛及复杂的非线性搜索过程；南杰琼等[2]提出的随机惯性权重(RIW)算法虽然加入随机扰动正弦调整粒子群的惯性权值以增强算法的搜索能力，但算法寻优时探测和开发能力的调节作用不甚明显；纪雪玲等[3]提出的收缩因子(CFPSO)算法虽引入速度因子和位置因子参数,但粒子向全局最优接近且速度小于设定的速度因子,粒子易出现停滞；付强等[4]提出的改进的加速遗传算法解决了在求解作物非充分灌溉下，灌溉模型优化过程易早熟及陷入局部最优，但却难于求解真正最优解；罗志平[5]提出自适应粒子群优化算法(APSO)应用在灌溉配水优化灌溉模型中可对算法的探测和开发能力进行调节，但作物各生育阶段间的灌水量并非最优效益分配。

在考虑工业、生活、环境供水量因素下，为使单位面积上作物的经济效益最大，本文提出一种改进随机惯性权重的粒子群优化算法MRIW(Modified Random Inertia Weight)，不仅能够解决粒子群算法收敛速度慢且易陷入局部最优解问题，而且MRIW算法应用在灌区进行寻优求解时，可使得灌区农业经济效益上有显著增长。

1 方法

1.1 模型建立

本文所讨论的优化配水模型是在已知目标函数下，使灌区整体农业效益最大。设灌区整体效益为F(元)，灌溉效益为Fi(元)。其中i=1,2,…,n(为了分析问题简单起见，假设该灌区有6条河)。公式:

(1)

(2)

式中，m表示种植作物种类数；Pij表示i支流j种种植物市场单价，元·kg-1；Yij表示i支流j种种植物总产量，kg；Cij表示i支流j种种植物供水费用，元·m-3；Mij表示i支流j种种植物667m2实际灌水总量，m3·hm-2；Sij表示i支流j种种植物种植面积，hm2。

本文选用生育期水分的抛物线关系函数模型[7]，公式：

yj(αj)=aj+bjM′j(αj)+cjM′j(αj)2

(3)

式中，yj(αj)表示第j种种植物实际非充分灌溉下667m2产量，kg·hm-2；M′j(αj)表示第j种种植物全生育期667m2实际总得水量，m3·hm-2；a、b、c表示第j种种植物全生育期水分生产函数经验系数。

将式(3)带入式(2)中，得出灌区在非充分灌溉条件下的农业经济效益函数[8]，公式：

(4)

结合实际情况，给出模型的约束条件[7]。

供水总量约束条件：

(5)

归一化系数约束条件：

0<αj≤1 (j=1…m)

(6)

支流供水最大承载约束：

(7)

支流最小供水量约束：

(8)

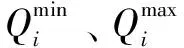
1.2 改进随机惯性权重的粒子群优化算法(MRIW)

Shi等人[8,9]定义的原始惯性权重w公式：

(9)

惯性权重w可调节PSO算法的全局与局部寻优能力。本文提出最优适应值变化率k公式：

(10)

式中，f(t)表示种群在第t代时的最优适应值；f(t-10)表示种群在第t-10代时的最优适应值；k表示在进化10代内最优适应值的相对变化率。

该改进策略有2个特点，w值将使粒子历史速度对当前速度的影响为随机的；w的数学期望值将随最优适应值的变化率自适应地调整，从而可以更灵活地调节全局搜索与局部搜索能力。

2 数据

参考近年来农业资料及其它相关资料可得，灌区主要种植的经济作物相关参数和灌区灌溉情况分别如表1、2所示。

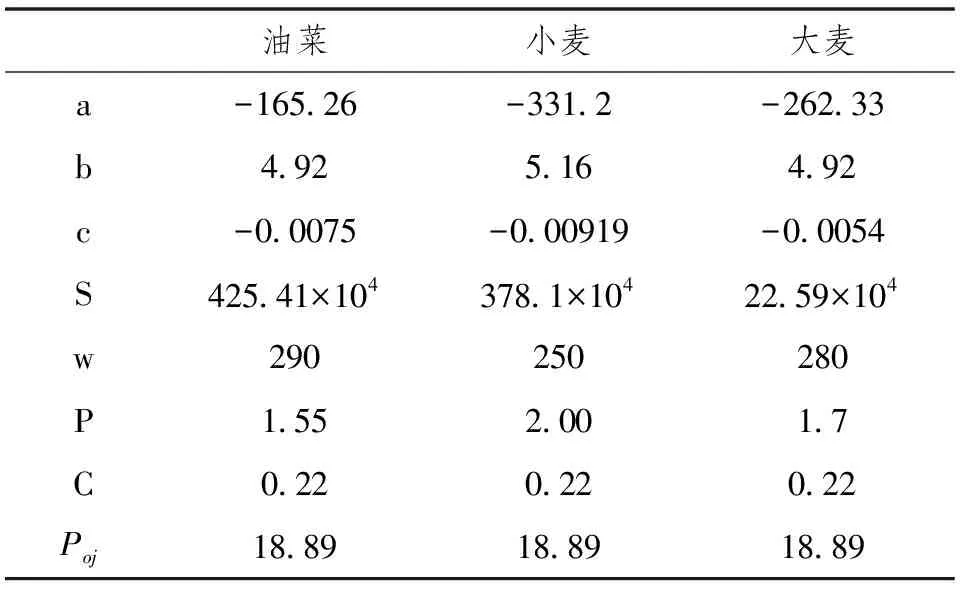
表1 主要作物参数表

表2 灌区支流灌溉情况一览表

3 仿真分析

3.1 各算法参数设置

粒子大小为求解维数，这里为4；群体规模取20；c1=c2=1.0；Tmax=100；wmax和wmin分别取0.9和0.2。对于MRIW算法，a1=0.7，a2=0.3；对于CFPSO算法，χ=0.7326；对于APSO算法，Dmax和Dmin分别取0.21和0.003，Emax和Emin分别取3.0和0.29，变异概率pm取0.01。

3.2 灌水处理设置

将270～350mm以间隔10mm为一个取值范围，采用LDW算法、CFPSO算法、APSO算法和MRIW算法进行寻优时最佳适应度值随进化代数变化的情况如图1～7所示。

从图1～7可以看出，MRIW算法在寻优时收敛速度最快，性能最好；MRIW算法寻优得到的作物单位面积净利润都比LDW算法、CFPSO算法、APSO算法大，再一次证明了MRIW算法的优越性。图8显示4种算法对模型进行优化求解时单位面积净利润随灌水量增加而增加，可见MRIW算法对有限灌水量进行优化分配都可得到较好效果。

4 总结

本文利用改进的蚁群算法对灌溉模型进行寻优求解，并以灌区为实例，将MRIW算法和LDW算法、CFPSO算法、APSO算法进行仿真比对发现，MRIW算法在寻优时收敛速度最快，性能最好，且算法在灌溉配水不同有限灌水量下，经济效益最优。因此，本文的研究可以为有限灌溉配水下作物效益最优提供较为科学的依据，指导作物节水灌溉实践。