非线性切换系统的异步事件驱动控制

孙韬，董潇潇

非线性切换系统的异步事件驱动控制

孙韬，董潇潇

（沈阳工业大学 理学院，辽宁 沈阳 110870）

事件驱动控制是一种减少通讯总量并能保持闭环系统性能的有效控制策略。在事件驱动控制中，由于取样时刻与切换时刻之间的异步会导致子系统与控制器之间的异步切换，造成切换系统的不稳定。因此，考虑非线性切换系统的异步事件驱动控制问题显得尤为重要。为了解决这一问题，首先从结构简单的线性部分和非线性部分级联的非线性切换系统入手，基于该系统的结构特点构造合适的Lyapunov函数。然后，针对每个子系统设计系统的切换控制器，并给出切换系统所要满足的平均驻留时间，当切换系统的切换信号满足一定平均驻留时间时，得到切换系统全局一致指数稳定的充分条件。最后给出数值算例消除了异步切换所导致的系统的不稳定性，说明了该方法的有效性。

事件驱动控制； 非线性切换系统； 平均驻留时间； 异步切换

切换系统是一类重要的混杂系统，自20世纪60年代起被引入控制理论中，并在飞行器控制、智能机器人、交通系统及电力发电系统得到广泛的应用[1-3]。为了改善系统的暂态性能，提高系统的控制精度，研究者们建立了切换系统的理论模型。目前切换系统的研究主要包括稳定性分析及设计问题[4-9]、能控及能观性问题[10-11]、无源性研究[12-13]、监督控制[14]等。其中，异步切换对切换系统影响的研究引起了越来越多学者的重视[15-17]。

在实际系统中，异步切换很容易导致切换系统不稳定，为获得良好的性能和所需的目标，有必要研究异步切换控制问题[18]。文献[19]研究了随机切换非线性系统的鲁棒异步切换控制。文献[20]给出了具有多面体不确定性切换时滞系统镇定的充分条件。文献[21]研究了异步切换非线性系统的鲁棒控制，当子系统满足驻留时间时，设计控制器使闭环系统状态呈指数收敛。事件驱动控制可以减少传感器、控制器和执行器之间大量交互中的系统信息负载问题。目前，越来越多的学者开始关注切换系统的事件驱动控制问题。M.Wakaiki等[22]提出了采用定期采样方法研究带有有限静态量化器的线性切换系统的稳定性问题。文献[23]将定期采样控制的研究结果扩展到线性切换中立系统中。现有的研究成果只给出了线性切换系统事件驱动控制问题可解的充分条件。然而，非线性切换系统的事件驱动控制研究结果还未见报道。

本文研究了异步切换下非线性切换系统的事件驱动控制问题。首先，针对控制器与子系统匹配和不匹配两种情况，分别构造Lyapunov函数。然后，设计子系统的镇定控制器。最后，切换系统满足一定平均驻留时间的切换信号作用下，得到切换系统全局一致指数稳定的充分条件。

1 问题描述

考虑如下级联非线性切换系统：

假设在切换中不产生系统状态跳变，则系统（1）的解是连续的。本文拟研究的系统（1）是非线性控制中一类常见系统，其中一个显著的优势是利用系统的部分状态进行反馈[24]。

引理1[27]给定一个适当维数的对称矩阵：

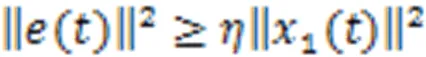
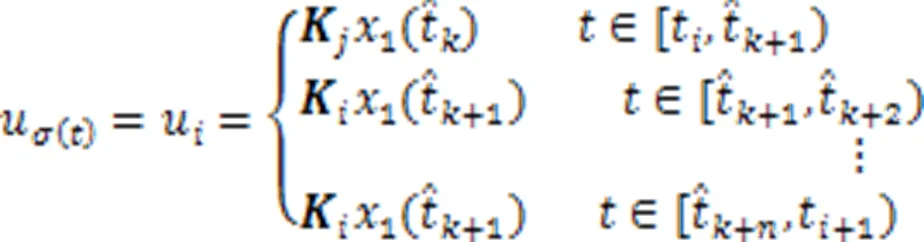
2 主要内容

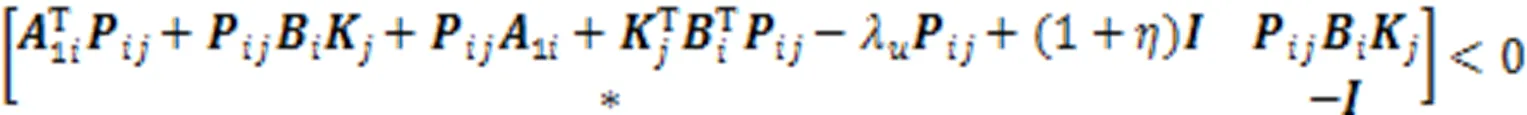
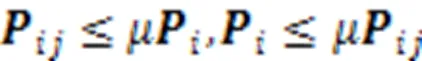
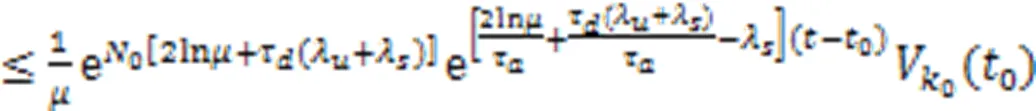
根据式（11）可得：

3 数值算例

图1　切换系统状态响应

图2　切换系统控制输入

图3　事件驱动条件

图4　事件驱动瞬间

切换信号如图5所示。从图5可以看出，控制器和子系统可发生异步切换。从仿真结果可知，系统在采样条件确定的控制输入下是稳定的。

4 结 论

针对非线性级联切换系统，研究了基于异步切换的事件驱动控制问题。设计了子系统状态反馈控制器获得闭环系统，针对子系统与控制器匹配和不匹配的情况，分别构造相应的Lyapunov函数，根据适当的切换信号，利用平均驻留时间的方法得出使闭环系统的全局一致指数稳定的充分条件。最后给出数值算例，证明了此方法的可行性。

图5　切换信号

［1］Gao Y， Wen J W， Peng L. New exponential stability criterion for switched linear systems with average dwell time［J］. Proceedings of the Institution of Mechanical Engineers， 2019， 233（8）： 935-944.

［2］Cheng J， Zhu H， Zhong S， et al. Finite-time filtering for switched linear systems with a mode-dependent average dwell time［J］. Nonlinear Analysis Hybrid Systems， 2015， 15：145-156.

［3］Spandan R， Simone B. On reduced-complexity robust adaptive control of switched Euler–Lagrange systems［J］. Nonlinear Analysis： Hybrid Systems， 2019， 34： 226-237.

［4］Ooba T， Funahashi Y. Two conditions concerning common quadratic Lyapunov functions for linear systems［J］. IEEE Transactions on Automatic Control， 1997， 42（5）： 719-721.

［5］Ana C C. Stabilization criteria of a class of switched systems［J］. Mathematical Methods in the Applied Sciences， 2019， 42（17）：5827-5833.

［6］Hong S S， Zhang Y. Stability of switched positive linear delay systems with mixed impulses［J］. International Journal of Systems Science， 2019， 50（16）：3022-3037.

［7］Cheng D Z， Feng G， Xi Z R. Stabilization of a class of switched nonlinear systems［J］. Journal of Control Theory and Applications， 2006， 31（1）： 53-61.

［8］Han M H， Zhang R X， Zhang L X. Asynchronous observer design for switched linear systems： A tube-based approach［J］. IEEE/CAA Journal of Automatica Sinica， 2020， 7（1）： 70-81.

［9］Wang Z C， Sun J， Chen J. Finite‐time stability of switched nonlinear time‐delay systems［J］. International Journal of Robust and Nonlinear Control， 2020， 30（7）：2906-2919.

［10］ 张嘉恬.异步切换下线性系统的稳定性分析［D］.沈阳：沈阳师范大学， 2019.

［11］ Luo S， Deng F， Zhang B， et al. Almost sure stability of hybrid stochastic systems under asynchronous Markovian switching［J］. Systems & Control Letters， 2019， 133：104556.

［13］ 柳硕，庞洪博.非线性切换系统的拟无源和反馈拟无源化［J］.渤海大学学报（自然科学版）， 2018， 39（4）： 303-308.

［14］ 李阳，赵晓颖，常东超. 一类状态受控椭球特性的时滞系统的鲁棒控制［J］.辽宁石油化工大学学报， 2019， 39（1）： 77-81.

［15］ Wang Y E， Wu B W， Wu C. Stability and L2-gain analysis of switched input delay systems with unstable modes under asynchronous switching［J］. Journal of the Franklin Institute， 2017， 354（11）： 4481-4497.

［16］ Fei Z， Shi S， Zhao C， et al. Asynchronous control for 2-D switched systems with mode-dependent average dwell time［J］. Automatic， 2017， 79： 198-206.

［17］ Cheng J， Zhu H， Zhong S， et al. Finite-time filtering for switched linear systems with a mode-dependent average dwell time［J］. Nonlinear Analysis Hybrid Systems， 2015， 15：145-156.

［18］ 赵亚茹，黄振坤. 时标上切换系统在异步切换下的稳定性分析［J］. 集美大学学报（自然科学版）， 2019， 24（6）： 463-470.

［19］ Xiang Z， Chen Q. Robust reliable control for uncertain switched nonlinear systems with time delay under asynchronous switching［J］. Applied Mathematics and Computation， 2013， 216（3）：800-811.

［20］ Wang R， Shi P， Wu Z G， et al. Stabilization of switched delay systems with polytopic uncertainties under asynchronous switching［J］. Journal of the Franklin Institute， 2013， 350（8）：2028-2043.

［21］ Xiang Z R， Wang R H. Robust control for uncertain switched non-linear systems with time delay under asynchronous switching［J］. IET Control Theory & Applications， 2009， 3（8）：1041-1050.

［22］ Wakaiki M， Yamamoto Y. Stability analysis of sampled-data switched systems with quantization［J］. Automatica， 2016，69： 157-168.

［23］ Fu J， Li T F， Chai T， et al. Sampled-data-based stabilization of switched linear neutral systems［J］. Automatica， 2016， 72：92-99.

［24］ Sepulchre P， Jankovic M， Kokotovic P. Constructive nonlinear control ［M］. London：Springer-Verlag， 1997.

［25］ Li T F， Wang H. Asynchronous switching control for switched delay systems induced by sampling mechanism［J］. IEEE Access， 2017， 56（99）：1-10.

［26］ Lu A Y. Analysis and control of a class of switching systems with dwell time［D］. Boston：Northeastern University， 2017.

［27］ Huang Y L， Lin S R， Yang E . Event-triggered passivity of multi-weighted coupled delayed reaction-diffusion memristive neural networks with fixed and switching topologies［J］. Communications in Nonlinear Science and Numerical Simulation， 2020， 89：105292.

Asynchronous Event-Triggered Control of Cascade Nonlinear Switched System

Sun Tao， Dong Xiaoxiao

（College of Science，Shenyang University of Technology，Shenyang Liaoning 110870，China）

In order to obtain good performance and required goals, the existence of asynchronous switching of controllers and subsystems must be considered. The event-triggered control of nonlinear switched system under asynchronous switching is studied. As the switching of the controller lags behind the switching of the subsystem, asynchronous behavior occurs. First, the switched nonlinear systems with linear parts and nonlinear parts are researched and the Laypunov functions are constructed. Then, a switching controller for a cascaded nonlinear switched system to obtain a closed-loop system is designed, and the average dwell time is given to get the sufficient condition for the switched system to be globally uniformly and exponentially stable. Finally, a numerical example is given to illustrate the feasibility of the method.

Event-triggered control； Nonlinear switched system； Average dwell time； Asynchronous switching

TP13

A

10.3969/j.issn.1672-6952.2021.04.015

1672-6952（2021）04-0091-06

http：//journal.lnpu.edu.cn

2020-04-29

2020-05-19

国家自然科学基金项目（61503254、61673099）。

孙韬（1995-），女，硕士研究生，从事切换系统的分析与控制方面的研究；E-mail: echigen@qq.com。

董潇潇（1983-），女，博士，副教授，从事切换系统分析与控制等方面的研究；E-mail:dongxiaoxiao1983@163.com。

（编辑 陈 雷）