频谱感知中的K-D树KNN-SVM算法研究

蒋礼君，张晓格，2

（1.南通大学 信息科学技术学院，江苏 南通 226019；2.南通先进通信技术研究院有限公司，江苏 南通 226019）

0 引 言

认知无线电是针对通信射频环境中频谱资源稀缺问题，提出的一种解决方案，旨在提高整体频谱资源利用率[1]。研究表明，当授权频段未被授权用户占用时，频谱感知技术为未授权用户在不影响授权用户使用的情况下，占用授权频段频谱提供了可能。未授权用户可单独或协作地感知当前频谱的状态，进而评估授权用户的存在与否[2-3]。认知无线电的概念最早是由JosephMitolaⅢ于1999年提出的，频谱感知在检测授权用户的过程中仍然充满挑战，因为频谱感知性能通常与检测率、虚警率以及检测时间相关。检测率越高，虚警率越低，则感知性能越佳。若感知时间越长，其时效性也会随之下降，进而影响频谱感知性能。图1从单节点感知和协作感知两个角度分别介绍了频谱感知的技术分类。传统的频谱感知算法有能量检测、循环平稳检测、特征值检测、匹配滤波检测等[4]。

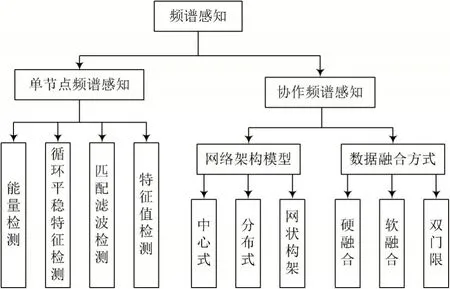
图1 频谱感知技术分类

随着机器学习受到越来越多的关注，并且在许多领域中得到了应用。很多专家学者们把机器学习应用到频谱感知[5]。机器学习通过复杂的计算，实现学习、推理和决策，是一种利用样本数据，优化系统性能指标的方法，具有评估和解释模式的能力。机器学习算法可以解决现实中大量的非线性分类问题，包括非线性回归和分类问题。因而从分类的角度看，机器学习及其相关的理论完全具备解决频谱感知问题的能力[6]。

基于现有的机器学习频谱感知算法，本文提出了一种K-D树KNN-SVM联合分类器的频谱感知算法，可以进一步提高频谱感知中对授权用户的检测率，同时降低虚警率。本文分析研究了KNN与SVM各自的优缺点，即KNN在大样本的情况下，计算开销大，SVM在分类超平面附近的样本分类容易出错。因此，通过KNN算法将分类超平面附近的样本信息充分利用起来，从而提高频谱感知检测率。KNN在计算的过程中，有部分计算是没有必要的。运用K-D树KNN，将训练样本排列成二叉树的结构，可以省去多余的计算，有效地降低了训练时间和分类延迟[7]。文献[8]提出一种LSTM神经网络分类器，无需估计检测门限值，也无需构造特征向量。文献[9]提出一种先利用PCA对信号能量最大的循环谱特征进行降维，再利用训练好的XGBoost算法对信号进行分类。文献[10]提出一种在随机检测理论基础上，利用双门限对传统最大最小特征值（MME）算法进行改进。文献[11]提出一种通过强化学习的方法，有效识别恶意用户，使其逐渐退出感知网络，使协作频谱感知网络更具智能性和稳定性。文献[12]提出一种在协作感知网络中，通过遗传算法对权值的优化，实现对每个感知节点设定合适的感知门限进行优化。文献[13]提出了一种基于SVM的协作频谱感知模型，该模型利用用户分组的方法来减少协作开销并有效地提高检测性能。在协作感测过程之前，使用能量数据样本和SVM模型对认知无线电用户进行正确分组。文献[14]提出一种基于贝叶斯机器学习的新框架，利用多个SU的移动性来同时收集频谱感知数据并合作得出全局频谱状态。

1 系统模型

频谱感知的目的是发现空闲信道频段，从而提高频谱资源利用率。实现的方法是对收到的信号采样、检测，进而分类出当前授权频段内是否存在主用户信号。频谱感知可以看作是一个二元分类问题。设H0表示主用户信号存在，H1表示主用户信号不存在，则接收信号为：

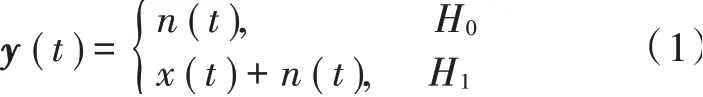
对该时域上的信号y(t)以频率为fs进行采样，可得到时域离散信号为：

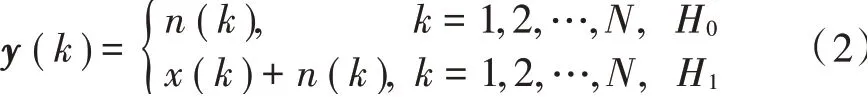
式中：y(k)为认知节点接收到的信号；x(k)为主用户信号；n(k)是均值为0、方差为σ2n的高斯白噪声，n(k)与x(k)彼此独立。接收信号的样本协方差矩阵可以表示为：

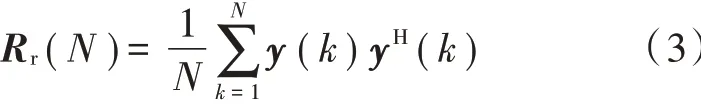
基于接收信号的协方差矩阵特征值检测法首先对接收信号进行采样，求出信号样本的协方差矩阵Rr(N)，进而得到矩阵的特征值。根据不同的算法构造出不同的检测统计量T，再根据系统所需达到的虚警率Pf，计算出实际的判决阈值γ。将检测统计量T和阈值γ进行比较，判断当前频段是否存在授权用户信号。

在协方差矩阵MME算法中，λMAX，λMIN为接收信号协方差矩阵的最大和最小特征值。检测统计量TMME为：

将信号协方差矩阵分解，求解矩阵特征向量作为联合分类器算法的特征向量输入到K-D树KNN-SVM联合分类器中训练。相比传统的特征值检测法，不需要计算信号的统计判决量T来与检测阈值γ相比。

根据授权用户是否存在，将授权用户不存在情况下的特征向量T0标记为负类样本，即属于“-1”类；将主用户存在情况下的特征向量T1标记为正类样本，即属于“+1”类。此时的训练样本就由正类样本和负类样本组成。将此样本集输入到K-D树KNN-SVM联合分类器模型中，完成训练。

2 K-D树KNN-SVM联合分类器

2.1 K近邻分类器

KNN是一种基本分类与回归的方法，一般是用来解决分类问题。它的输入为待分类样本特征向量，输出为待分类样本类别，可以取多类。KNN假设给定一个训练样本集，其中各样本类别已定。对于待分类样本x，遍历与训练样本之间的距离。若与x最邻近的样本i属于某一类别ωi，则x也属于ωi类。

为了提高KNN的准确率，选择与待分类样本x距离最近的k个样本，通过投票方式进行决策。若ωi为k个类别中票数最高的类，则x也属于ωi类。

2.2 近邻的距离度量表示法

K近邻模型的特征空间一般是n维实数向量空间。特征空间中不同样本之间的距离反映样本之间的相似程度。两个样本之间的“距离”越近，则相似度越高。一般而言，定义一个距离函数D(x,y)，需要满足对称性、非负性、自反性和三角不等式这4个准则。以下是距离的定义公式：

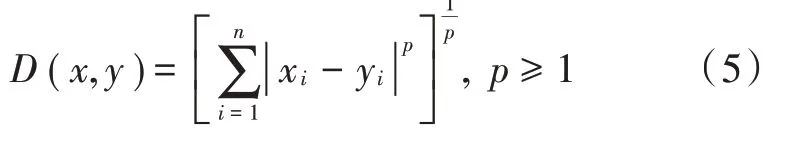
称为闵可夫斯基距离。当它满足上述定义的4个距离准则时，随着对应的矢量范数p的不同，代表的距离度量也不同。

当p=2时，表示为欧氏距离：

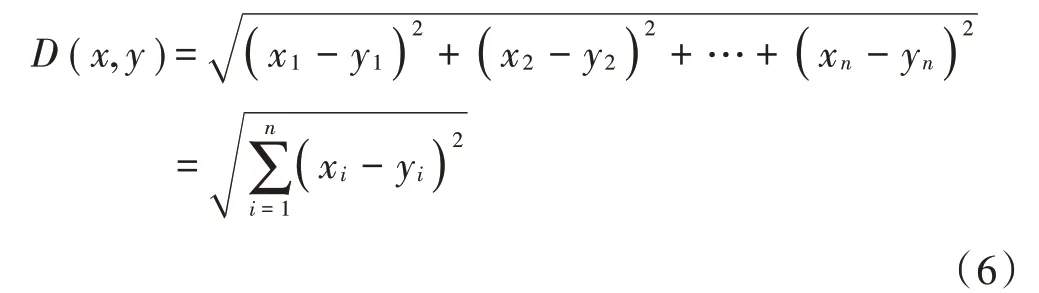
当p=1时，表示为哈曼顿（街市）距离：

当p=∞时，表示为切比雪夫距离：

一般情况下，根据数据可选择最佳的k值。若选择较小的k值，容易发生过拟合，整体模型变得复杂，导致模型学习的估计误差增大。若选择较大的k值，类别之间的界限会变模糊，增大模型学习的近似误差。在实际应用中，k先取一个比较小的数值，再采用交叉验证法来逐步调整k值，最终选择适合该样本的最优的k值。

从算法的实现过程中可发现，该算法的优点是实现起来较为简单，缺点是需存储全部的训练样本且计算量较大，对于每一个待分类样本，都需遍历其与所有已知样本的距离，才能求得它的k个最近邻点。

2.3 K-D树KNN

2.3.1 K-D树的简介

K-D树是一种分割d维数据空间的数据结构，主要应用于多维空间关键数据的搜索，如范围搜索和最近邻搜索。在对d维样本空间进行划分时，用垂直于坐标轴的超平面将d维空间切分，构成一系列的d维超矩形区域，K-D树的每个节点对应于一个d维超矩形区域。因此利用K-D树可以省去对大部分无用数据点的搜索，从而减少搜索的计算量。对于具有k维点的K-D树，所有非叶子节点都存在于被分成两部分的平面空间内，平面左侧的点是左子树的节点，平面右侧的点是右子树的节点。

2.3.2 基于信号样本协方差矩阵特征向量建立K-D树

在获得接收信号样本的协方差矩阵特征向量，并将其导入到模型后，它们将被视为K-D树的节点，分为根节点和叶子节点。对于由n个d维数据组成的样本集，任意样本和任意维度的特征值都可以作为根节点，但为了确保以最快的速度搜索到最近邻，需构造一个均衡的二叉树。可通过以下方法建立均衡K-D树：

1）确定根节点

对于所有样本点，计算每个维度的方差，选出与最大方差相对应的维，称之为分割轴。然后所有样本点均按分割维排序，位于中间的数据点作为根节点，也称分割节点。

2）确定左右子树

将某一点与相同维中的分割节点的值进行比较，若该节点的值大于分割点的值，则应将该节点放入分割节点右侧的子树中；相反，若该节点的值小于分割节点的值，则将其放入左侧的子树中。

3）递归过程

按照方法2）中建树方法，递归左子树和右子树，直到所有数据都组建在一棵树中，即子集中只含有一个样本时，退出递归过程。

至此已完成建立基于信号样本的协方差矩阵特征向量K-D树，以上操作可使得样本有序化。其中，分割轴与分割超平面相互垂直，交点为样本在分割轴的特征值。对于n个d维的样本，K-D树实际上就是将样本d维的特征空间划分为n个互不相交的区域。因此，可以快速地找出样本x属于d维空间的那个区域，进而得到样本x的分类属性。

图2展示了K-D树算法的搜索流程，适用于训练样本数量远大于样本空间维数的情况。将最近邻搜索的时间复杂度从暴力搜索的O(n)降低至O(log2n)，搜索经过的节点与识别目标样本点距离最接近的样本，不一定是识别目标样本x的最近邻。因此，通过回溯过程，可以找到真正的最近邻样本。

图2 K-D树算法搜索流程

2.3.3 K-D树的最近邻搜索算法

输入：已构造的K-D树，识别目标样本x。

深度搜索：

1）在K-D树中找出包含识别目标样本的叶节点，从根节点出发，递归向下访问K-D树。若目标点当前维的坐标值小于分割点的坐标值，则移动到左子节点，否则移动到右子节点。直到子节点为叶节点为止。

2）以此叶节点为“当前最近邻点”。

回溯，递归向上回退，在每个回退样本节点进行以下操作：

1）如果回退样本节点保存的样本点比当前最近邻点距目标点更近，则以该回退样本点为“当前最近邻点”。

2）“当前最近邻点”一定存在于回退样本节点中某一子节点对应的区域，需要回退到样本子节点的父节点，检查该父节点的另一个子节点对应的区域是否有更近的点。以目标点为球心，以与“当前最近邻点”间的距离为半径，检查是否与此超球体相交。若相交，在另一个子节点对应的区域内存在距离目标更近的点，移动到另一个子节点，递归地进行最近邻搜索。

3）如果不相交，向上回退。4）当回退到根节点时，搜索结束。输出：最近邻样本节点和分类属性。

2.4 SVM分类器

SVM算法又被称之为大间距分类器算法，在线性不可分的情况，也能正确分类。它的目的在于找到一个超平面，在分离数据的时候，尽量用最大的间距去分离。优化目标函数可表示如下：

需满足约束条件：

此外，通过引入松弛变量ξi，使得分类器对异常值点不过于敏感。因此，最终的优化目标函数为：

且满足约束条件：

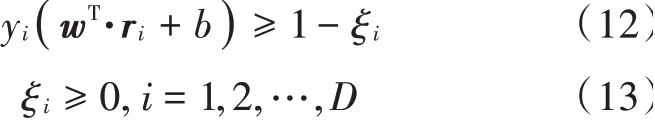
通过拉格朗日乘子法优化此问题，如下所示：

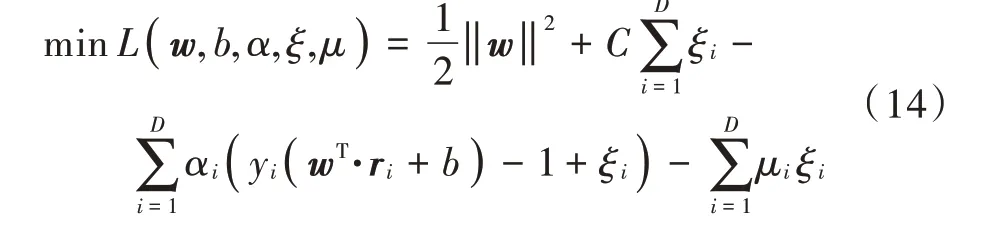
根据Karush-Kuhn-Tucker（KKT）条件，分别对w和b求偏导，可以得出：

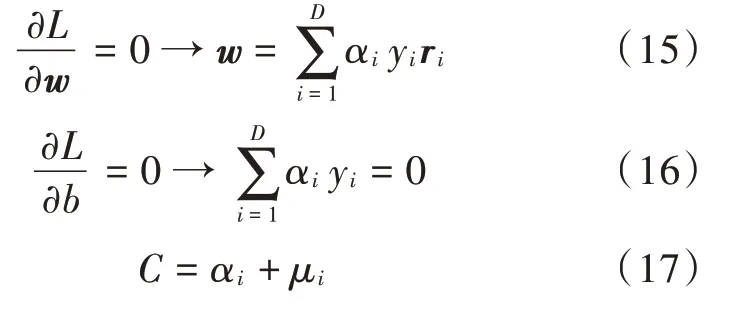
再将求出的极值点代入，进一步可简化为对偶问题：

满足约束条件：

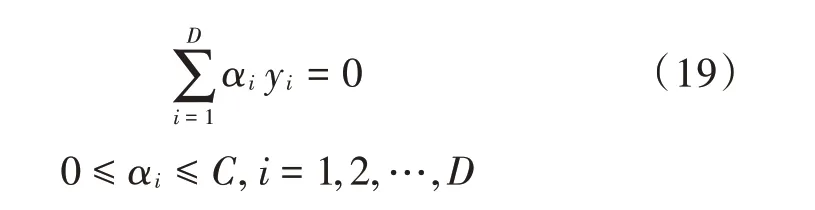
输入样本的向量和标签，得到一个关于αi的表达式，再通过求导的方法得出最优解α*，将其值代入后，可以求得最终得到分类边界。

由于实际情况下样本大部分都是非线性可分的，非线性决策边界若构造一个复杂多项式特征集合，会大大增加计算开销。因此，通过核函数的方法，将样本从原始空间映射到高维特征空间，实现样本在高维空间内线性可分。所有核函数都必须满足默塞尔定理。本文采用的是高斯核函数k(r i,r j)=rTi r j，在使用前需将特征向量进行归一化处理。运用二次规划算法求解凸优化问题，即可得到分类函数：

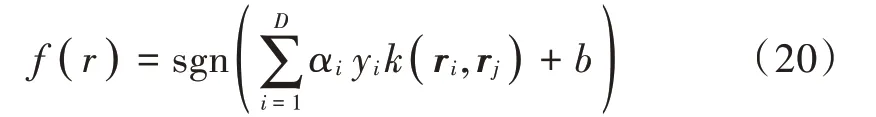
式中sgn(·)为符号函数。若f(r)=1，则认为主用户存在；相反，f(r)=-1，则认为主用户不存在。

2.5 K-D树KNN-SVM联合分类器

通过对以上算法的研究，可得出SVM和KNN各自的优缺点。SVM使用核函数向高维空间进行映射，可解决非线性问题的分类。在超平面附近样本易混淆时，KNN充分利用分类超平面附近的样本信息，通过计算待分类样本与已分类样本之间距离，虽然提高了分类的准确率，但遍历了与所有样本的距离，存在冗余计算。因此，结合这两种算法的优缺点，构造出改进的基于K-D树的KNN-SVM联合分类器算法。将训练样本构造成均衡的二叉树结构，可大大缩短搜索时间，从而提高搜索效率。

K-D树KNN-SVM联合分类器的算法流程如图3所示。

图3 K-D树KNN-SVM联合分类器算法流程

本文中K-D树KNN-SVM算法的具体步骤如下：

1）先采用支持向量机算法对分类样本测试集进行训练，可得出相应的参数以及对应的支持向量SV。

2）得到支持向量机的输出值：

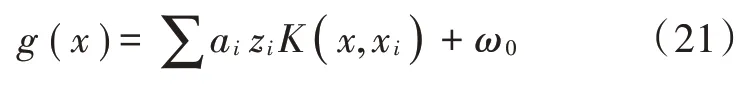
4）若|g(x)|＜ε，算法将传递参数x和SV，把SV当作训练集输入到K-D树KNN算法中进行分类，输出分类结果。

分析可得，当E=0时，该算法等价于SVM算法，E的值需要根据实际的分类结果来进行调整，进而得到最优值。特征空间下的超平面不再是SVM的分类超平面，计算训练样本和每个支持向量之间的距离公式不再是SVM样本空间下的欧氏距离公式，改为式（22）来计算特征空间中的距离：

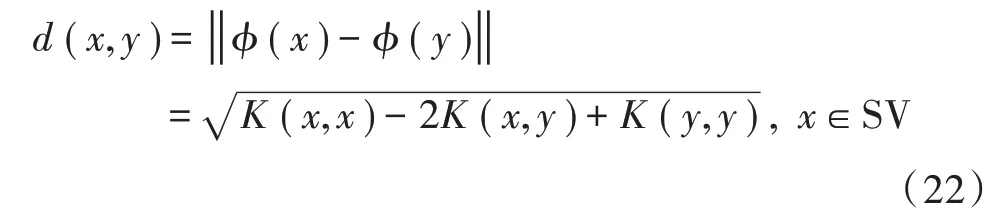
该算法采用的核函数为高斯核函数，能有效降低算法的复杂度，从而提升检测效率。高斯核函数以及原样本空间下的欧氏距离公式为：

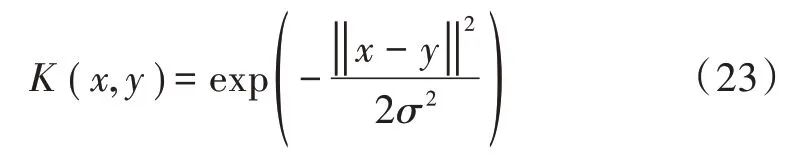
在使用高斯核函数映射后的欧氏距离D(x,y)和原样本空间下的欧氏距离d(x,y)的表达式为：

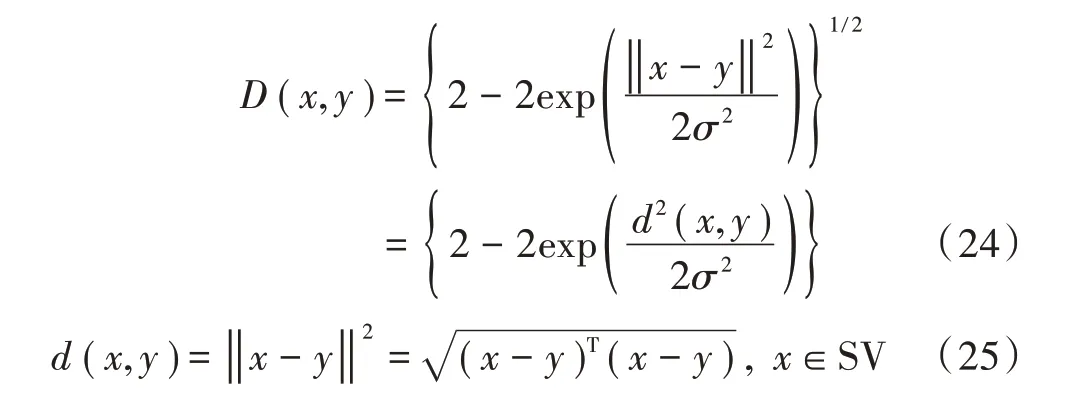
从式（24）、式（25）的单调性来看，D(x,y)是d(x,y)的单调增函数，原样本空间下与特征空间下样本相对应的位置并没有发生变化，变化的只是样本之间的紧密度，因此二者的使用效果是相同的，样本之间的近邻关系也完全相同。

3 仿真结果与分析

频谱感知算法性能的指标包括虚警率、检测率和检测时间。当给定系统要求的虚警率时，检测率越高，检测时间越短，则频谱感知算法的性能越佳。

在AWGN信道环境下，实验仿真基于Matlab R2016a。首先利用Matlab产生授权用户存在与不存在情况下的模拟信号，分别进行采样得到离散信号，再提取离散信号的协方差矩阵特征向量，得到训练样本和测试样本。其中，75%为训练样本，25%为测试样本。调用Matlab中的LibSVM-3.24算法模块，进行K-D树KNNSVM联合分类器算法的训练，训练完成后，使用训练好的模型对测试样本进行测试，输出信道中授权用户存在与否的分类结果。

具体实验参数设置如下，假设授权用户信号为正弦信号，载波频率fc为5 kHz，信噪比设置为5～25 dB。噪声信号为加性高斯白噪声，均值为0，方差为1。分别采用100帧，200帧，…，1 100帧来对比不同采样点数情况下的算法性能，其中每帧包含10个采样点。SVM的核函数选择高斯核函数，其中超参数的设置通过交叉验证得到，E的取值为1.06，KNN与KNN-SVM中的K值选择为13，K-D树KNN-SVM中的K值选择为6。不同采样点数下的检测时间对比如图4所示。

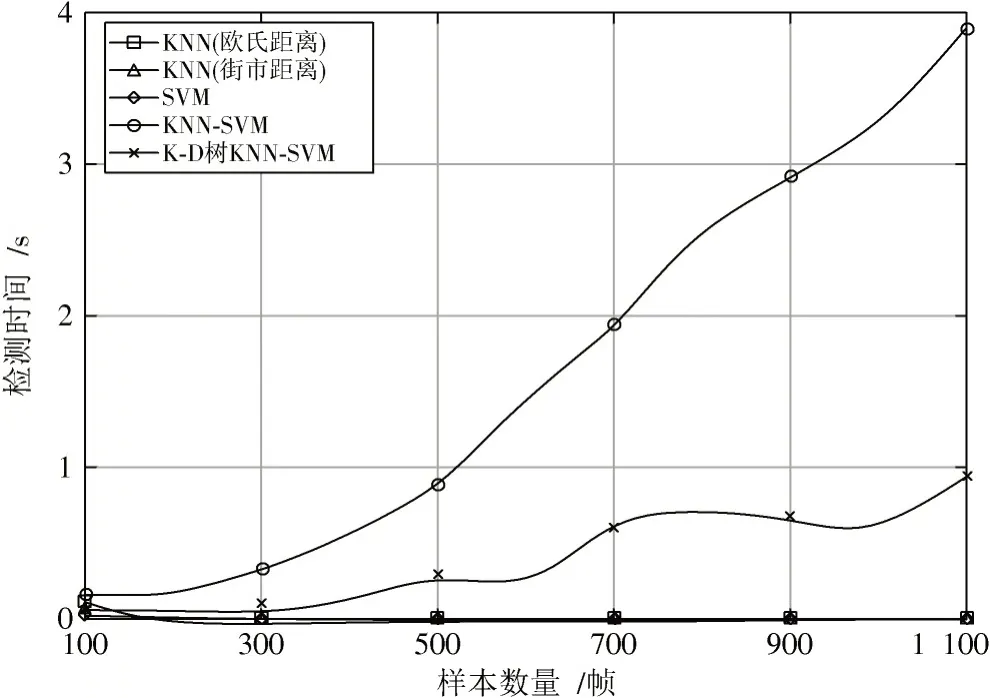
图4 不同采样点数下的检测时间对比

根据图4可看出，传统SVM与KNN检测时间均在0.003～0.004 s之间，当增大采样点数时，检测时间仍小于KNN-SVM联合分类算法。因为联合分类器算法在计算复杂度上，均比单一的SVM和KNN复杂，这也符合算法客观规律。而采用优化结构的K-D树KNN-SVM联合算法相比无优化的KNN-SVM算法，明显缩短了检测时间，因为经过K-D树结构优化后，使得KNN算法部分提升了搜索效率，缩短了检测时间。不同信噪比下的检测时间对比如图5所示。

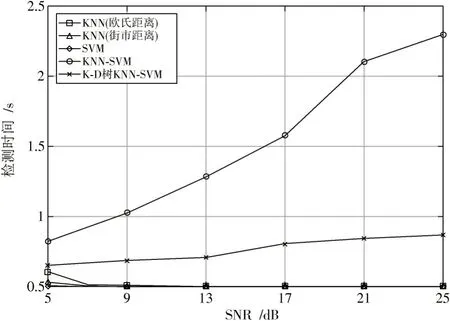
图5 不同信噪比下的检测时间对比

根据图5可看出，随着信噪比的提高，信号间的相关性较大，虽降低了特征提取难度，但使用K-D树优化结构的KNN-SVM算法相比无优化结构的KNN-SVM算法，仍可明显缩短检测时间。原因在于无优化结构搜索近邻上花费了较多时间，从而使得检测时间增加。优化结构之后在搜索近邻时，搜索时间差距不明显，检测时间趋于稳定。不同信噪比下的检测率对比如图6所示，虚警率对比如图7所示。

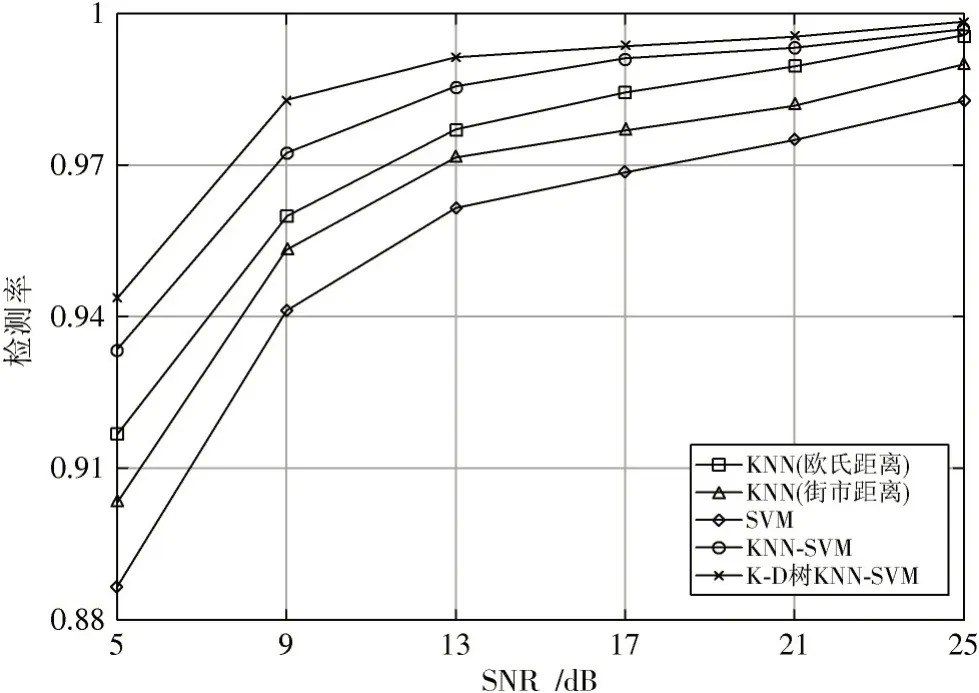
图6 不同信噪比下的检测率对比

根据图6和图7可看出，当KNN算法使用欧氏距离来寻找最近邻时，其检测性能优于使用街市距离（哈曼顿距离）。该算法提升了检测性能，降低了虚警率，提高了检测率。表1、表2分别为5 dB，25 dB处算法性能对比表。

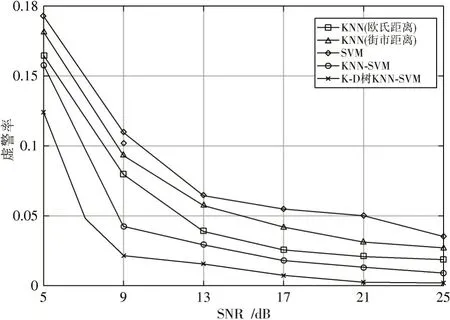
图7 不同信噪比下的虚警率对比

由表1和表2可看出，K-D树KNN-SVM联合分类器算法检测性能均优于单一的机器学习频谱感知算法。相比无优化结构的KNN-SVM算法，在5 dB处其检测率提高了1.05%，虚警率降低了2.86%；在25 dB时，检测率提升了0.14%，虚警率降低了0.006 2%。体现出该算法在检测性能上的优越性。

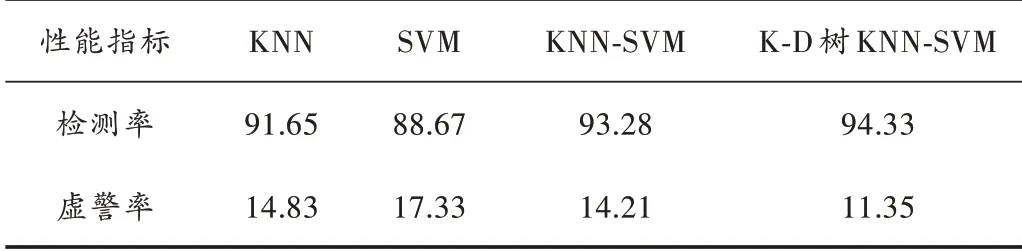
表1 5 d B处算法性能对比表 %

表2 25 d B处算法性能对比表 %

4 结 语

几种传统的频谱感知检测法，如能量检测法、特征值检测法，二者都需要计算出一个准确的决策阈值，阈值直接影响分类结果准确率，一旦分类阈值不准确，检测性能将会受到影响。再如匹配滤波检测法、循环平稳检测法，前者需要了解信号的先验信息，后者采集数据时间较长，计算复杂度较高，此外还会受到采样时偏的影响，影响检测准确率。本文构造的K-D树KNN-SVM频谱感知算法，不仅降低了检测的计算复杂度，无需计算决策阈值，也不需了解信号先验信息，只是将样本数据输入到分类器模型中，通过对历史数据的学习，从而实现频谱感知。

KNN-SVM提取支持向量机分类界面的模糊样本，使用KNN的方法进行再分类，充分利用分类面附近的样本信息，从而提高支持向量机的检测率。最后，通过仿真比较KNN-SVM和采用K-D树结构的KNN-SVM，发现采用K-D树结构的KNN-SVM联合分类器明显提高了检测率，降低了检测时间和虚警率，证明了该方法的有效性。