一种基于AES 和ECC 的混合密码技术的研究
尤紫云,刘晓东
(1.武汉邮电科学研究院,湖北武汉 430070;2.武汉虹旭信息技术有限责任公司,湖北 武汉 430070)
由于网络的广泛应用,信息安全[1]已成为保障网络环境的关键因素。在网络上有效地安全传输数据信息,保证信息的真实性、完整性和不可抵赖性是数据加密技术[2]的重中之重。
在对称加密算法中,如AES 算法,具有速度快、加密强度高、便于实现的优点,但是依然存在局限性,此算法的密钥分配与管理[3]比较困难。而非对称加密算法的密钥分发与管理简单并且有更高的加密强度,但是运算速度较慢。因此,将对称加密算法和非对称加密算法相结合,弥补各自算法的局限。因此文中提出基于AES 算法和ECC 算法的混合加密方案[4],采用AES 算法对明文加密,而ECC 算法加密管理密钥实现数字签名。该方案能有效地提高信息传输的安全性和效率,使网络传输变得更加安全可靠。
1 AES算法
1.1 AES算法结构描述
AES(Advanced Encryption Standard)可称为高级数据加密标准,属于对称加密算法[5],它也是一种基于分组迭代的加密算法。AES 算法的密钥长度可独立指定为128 bits,192 bits 或256 bits,在AES 数据加密标准中规范了明文分组长度为128 bits。
在AES 算法中数据块要经过多次数据变换,每一次变换产生一个中间结果,这个中间结果为状态。此状态可以用二维字节数组来表示,也就是一个状态矩阵,该矩阵的行数为4,列数Nb=分组长度/32。种子密钥也可以类似地用一个状态矩阵表示,同样以字节为元素,行数为4,列数Nk=密钥长度/32。Nb和Nk共同决定了算法的迭代轮数Nr,由于在AES 算法中分组长度固定128 bits,因此迭代的轮数可以由密钥长度推得。
AES 算法的轮函数采用的是SP(替代、置换)结构,每一轮由3 个层组成,每个层都是可逆并均匀变换的。1)非线性层:并行使用最优的S 盒,起到混淆作用,防止攻击者分析出密钥;2)线性混合层:通过行移变换和列混淆变换,以保证经过多轮变换之后能达到高度扩散,以防止统计分析的攻击;3)密钥加层:通过进行轮密钥加变换,将圈密钥异或到中间状态上,从而实现密钥的加密控制作用。
1.2 AES算法轮变换
AES 加密算法中的轮变换[6]由4 个部分组成,分别是字节代换(ByteSub)、行移变换(ShiftRow)、列混淆变换(MixColumn)、轮密钥加(AddRoundKey)。
每一轮都依次进行字节代换(S 盒变换)、行移变换、列混淆变换和轮密钥加。值得注意的是,加密算法的最后一轮没有列混淆变换。其中轮变换总体框架如图1 所示。
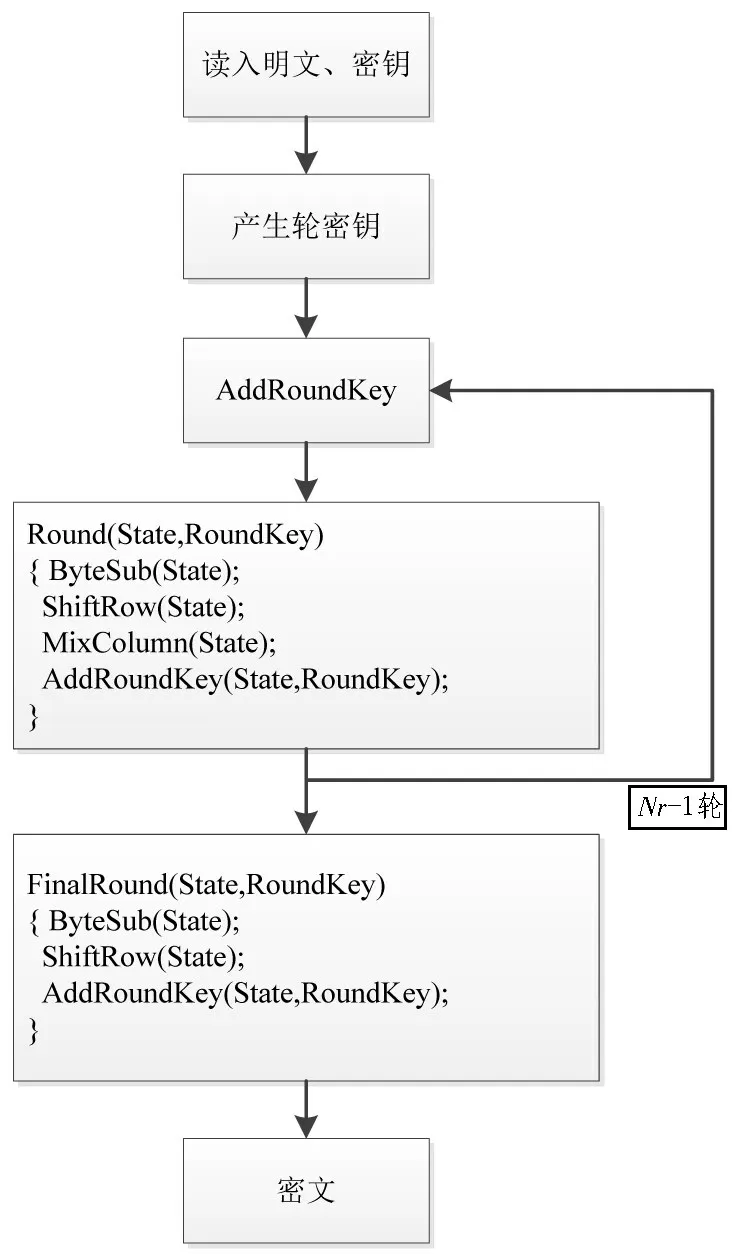
图1 AES轮变换框架图
1)字节代换
字节代换是将每个字节进行S 盒转换,达到非线性变换。它通过S 盒独立地对状态的每个字节进行变换,使字节高度混淆,步骤如下:1)将字节作为GF(28)上的元素映射到自己的逆元,实现有限域上的乘法逆;2)将每个字节作GF(2)上的仿射变换[7],即:y=Ax-1+B如式(1)所示,其中A是一个GF(2)上8×8的可逆矩阵,B是GF(2)上一个8 位列向量。
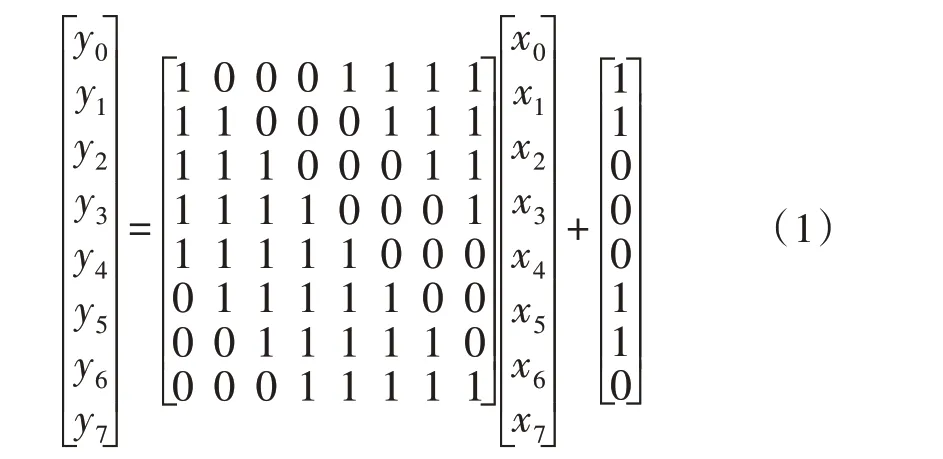
2)行移变换
行移变换是一种线性变换,它与列混淆变换结合使加密数据达到充分的混淆,它将状态矩阵中的各行循环移位若干位,移位量根据行数不同而改变。第0 行不需要移动,第1、2、3 行分别循环左移C1、C2、C3个字节。逆行移位变换是行移位变换的逆变换,它对状态的每一行进行循环右移。表1 为左移量与分组大小Nb的关系。
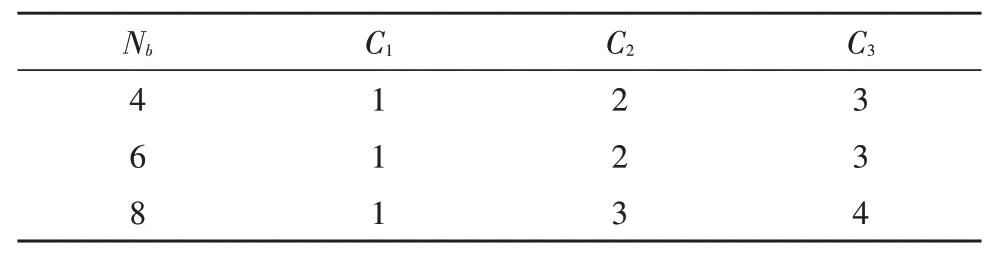
表1 左移量与分组大小Nb的关系
3)列混淆变换
列混淆变换为对状态矩阵中列的线性变换。将状态矩阵每列的4 个字节表示为GF(28)上多项式,再将该多项式与固定的多项式c(x)进行模x4+1 乘法,其中要求c(x)模x4+1 可逆。定义如下:
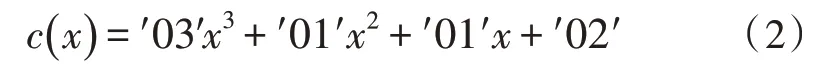
令b(x)=c(x)∙a(x)mod(x4+1),列混淆变换过程如图2 所示。
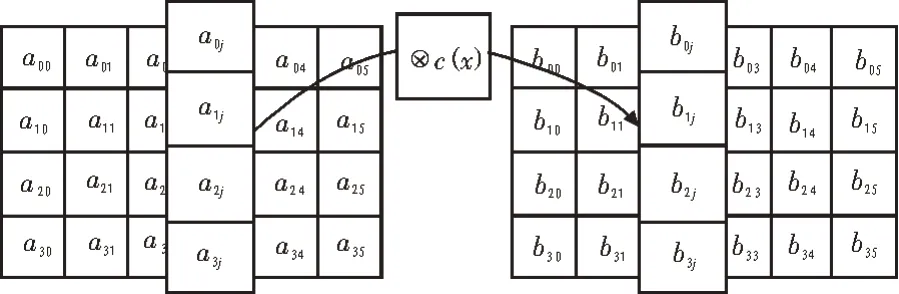
图2 列混淆变化示意图
4)轮密钥加
轮密钥加运算就是每轮的状态与对应的128 bits轮密钥进行逐比特异或。
2 AES算法的S盒优化
在AES 算法中实现数据的非线性置换[8]S 盒起到重要的作用,S 盒的设计有严格的数学计算,整个密码算法的安全性直接依赖于S 盒的安全性。
AES 算法S 盒的循环迭代周期比较短,遍历性有待提高,它的扩散性和表达式的复杂度并不能保证AES 算法在代数计算攻击中的安全性。现针对于上述S 盒性能的不足,将S 盒算法进行优化。
1)在有限域中对输入的字节元素求逆元。若两个元素相乘满足a(x)⋅b(x)modm(x)=1,就称b(x) 是a(x)的逆元,其中m(x)=x8+1 不变;
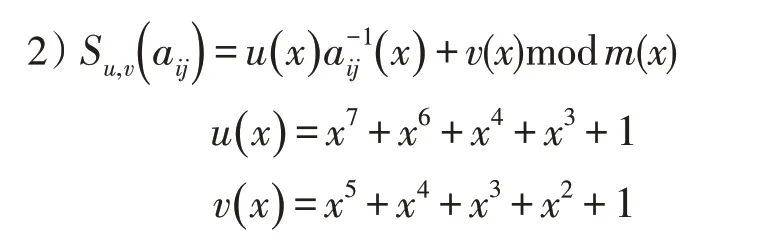
即取了一组新的仿射变换对(155,62);
3)运用新的仿射变换对,将字节作GF(2)上的仿射变换[9];
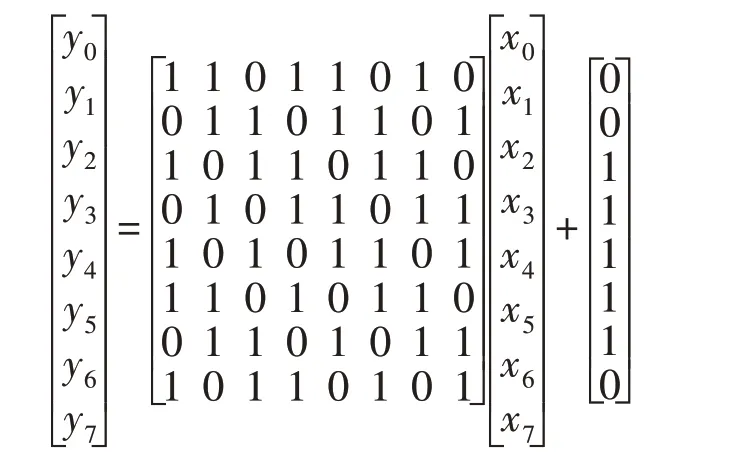
4)做乘法逆运算。
运用了新的仿射变换对使S 盒的循环迭代周期为256,GF(28)中所有元素只属于一个迭代循环。并将乘法逆运算和仿射变换的顺序交换,使得表达式长度增加到255 项,增加了代数计算复杂度,从而提高了算法的安全性。该文对原S 盒与提出的新S 盒的各项性能进行了比较,结果如表2 所示。
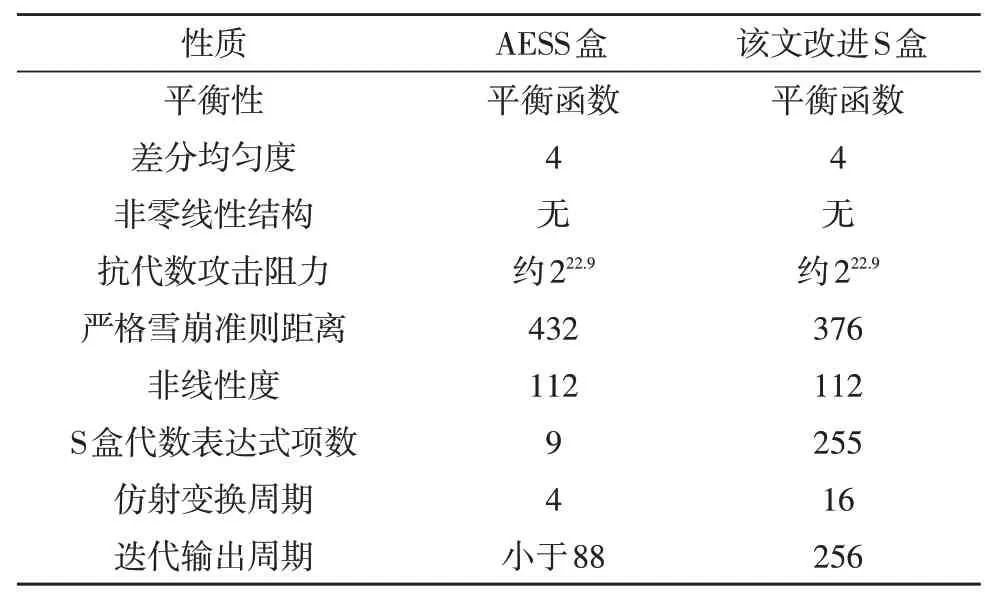
表2 两种S盒的对比分析指标
3 ECC算法
KOBLITZ 和MILLER 在1985年提出ECC(Elliptic Curve Crypto-system),称为椭圆曲线密码体制。与其他的公钥密码[10]如RSA[11]相比,在相同密钥长度下,椭圆曲线密码安全性更高,同时椭圆曲线密码更节约存储空间和算力。这主要得益于在椭圆曲线上离散对数问题[12]比有限域上的离散对数问题更难解。像一般的非对称加密算法原理那样,椭圆曲线密码也是基于“从a推导出b很难,从b推导出a容易”这样的模式实现了非对称加密。
3.1 有限域GF(p)上的椭圆曲线
椭圆曲线通常是指Weierstrass 方程所确定的曲线,它是由方程y2+axy+by=x3+cx2+dy+e的全体解再加上一个无穷远点O构成的集合。
在有限域GF(p)上,可以将上述曲线方程转化为y3≡x3+ax+b(modp),常记为Ep(a,b),简记为E。其中a,b,x和y均在有限域GF(p)上取值,p是素数,且满足4a3+27b2(modp)≠0。该椭圆曲线只有有限个点数n,表示为椭圆曲线的阶[13],其中n越大安全性越高。
3.2 椭圆曲线点的运算
当4a3+27b2(modp)≠0 时,称Ep(a,b)是一条非奇异椭圆曲线[14]。对于非奇异椭圆曲线上点得集合Ep(a,b)定义的加法规则构成一个群称为Abel 群[15]。规则如下:
1)单位元。O为加法的单位元,对于椭圆曲线上的任何一点P,有P+O=O+P=P。
2)逆元。对于椭圆曲线上的一点P=(x,y),它的逆元为-P=(x,-y),注意到P+(-P)=P-P=O。
3)点加。设P和Q是椭圆曲线上x坐标不同的两点,P+Q的定义如下:过点P和Q作直线l,直线l与椭圆曲线相交于唯一的点R,然后过R点作y轴的平行线l′,l′与椭圆曲线相交的另一点S就是P+Q,如图3 所示。
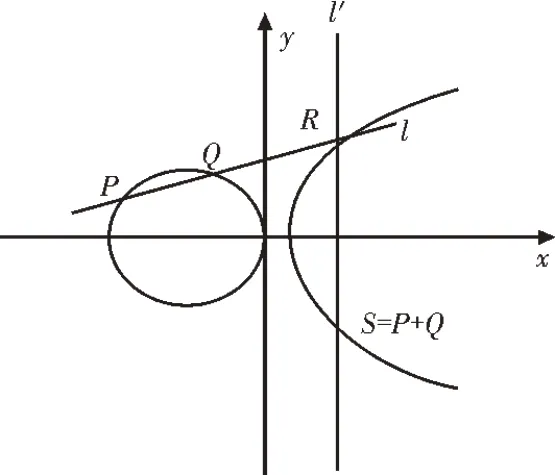
图3 椭圆曲线上点的加法的几何解释
4)倍点。为计算点Q的两倍,在Q点作一条切线并找到与椭圆曲线的另一个交点T,则Q+Q=2Q=-T。
4 AES和ECC混合密码算法
4.1 ECC算法密钥的生成
1)由椭圆曲线参数p,a,b来确定一条椭圆曲线,记为Ep(a,b);
2)在Ep(a,b)上选取基点G(x,y),且满足nG=0,其中n为G的阶(n为一个大素数);
3)选取一个整数Ks∈[1,n-1],通过计算Kp=Ks G,可以得到密钥对(Ks,Kp),其中Ks、Kp分别是私钥和公钥。
4.2 加密过程
明文使用AES 加密算法对其进行加密。AES 密钥加密采用ECC 加密算法对其加密生成密钥密文。其过程如下:
1)发送者选取一个随机整数r(r 2)将密钥明文用编码函数嵌入椭圆曲线Ep(a,b)上一点M=(mx,my); 3)计算C1=rG,C2=M+rKp; 4)向接收者发送(C1,C2)。 AES 密钥的解密过程如下; 1)接收者收到(C1,C2); 2)计算C2-KsC1=M+rKp-KsrG=M+rKsG-KsrG=M,可以得到点M; 3)再对M进行解码,得到AES 密钥。再结合AES 解密算法得到相应的明文。 1)数字签名的生成 假设发送者向接收者发送消息M并进行签名,发送者需执行以下步骤: ①任取一个整数k∈[1,n-1]; ②根据kG=(x1,y1),计算r=x1modn,若r=0,则回到步骤①; ③根据t=k-1modn,计算t的值; ④用Hash 函数SHA-1 计算Hash 值e=SHA(M); ⑤计算s=k-1(e+Ksr)modn,若s=0,则回到步骤①; ⑥发送消息M和它的签名(r,s)。 2)数字签名的验证 接收者接收到消息M和签名(r,s)后,接收者需执行以下步骤进行验证: ①验证r和s,需满足r、s∈[1,n-1]; ②计算e=SHA(M); ③计算w=s-1modn; ④计算u1=ewmodn和u2=rwmodn; ⑤计算U=u1G+u2Kp=(x2,y2); ⑥若U=0,则拒绝签名;若U≠0,计算v=x2modn; ⑦若v=r,则接收签名;若v≠r,则拒绝签名。 发送方: ①明文消息通过AES 加密算法的轮变换等进行加密,从而得到密文; ②再通过利用ECC 加密算法对AES 的密钥进行加密,从而得到AES 的密钥块; ③用发送者私钥在明文中提取消息摘要生成签名块; ④最后将密文、AES密钥和签名块传送给接收方。 数据加密具体流程图如图4 所示。 图4 数据加密流程 接收方: ①首先将AES 的密钥块通过ECC 解密算法进行解密,可以得到AES 密钥; ②然后将密文通过AES 密钥进行解密,从而得到明文消息,再进行SHA-1 算法[16]获得其信息摘要; ③用发送者公钥解密签名块生成摘要结果; ④比较两个摘要结果,若相等,则签名成功。 数据解密具体流程图如图5 所示。 图5 数据解密流程 由于互联网越来越被大众接受和使用,人们对信息安全保护的需求越来越迫切,该文提出一种基于AES 和ECC 的混合密码技术,具备了两种算法的优点:储存空间小、运算速度快、密钥管理方便等。从而可以高效地实现了互联网中的信息加密、数字签名和身份认证,解决了密码体制中速度和安全性不能兼顾的问题。同时重新设计了AES 算法中的S盒,改进的S 盒的循环迭代周期扩大到256,提高了遍历性,表达式长度增加到255 项,增加了代数计算复杂度,从而提高了算法的安全性。4.3 解密过程
4.4 数字签名的生成和验证
4.5 混合算法流程图
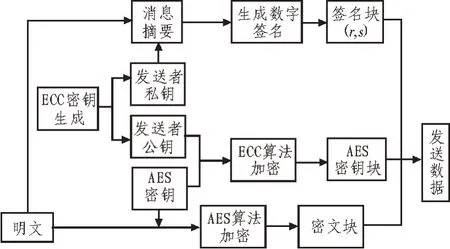
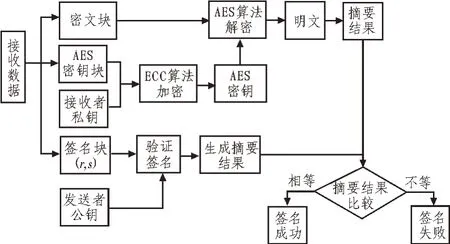
5 结束语

