基于GARCH族模型的沪深300指数波动性研究

陈 苍 赵志琴

（广州新华学院，广东 广州 510520）

股票市场作为我国金融市场的重要组成部分，能有效预示和推动经济发展。与发达国家相比，我国股票市场因起步晚尚不成熟，股票市场的波动性较为强烈。但中国股票市场对世界股票市场的影响越来越大，因此我们有必要对股票市场的波动情况进行研究。GARCH模型是研究具有集群效应金融数据波动性的有效办法，TGARCH模型侧重研究金融数据波动性是否具有非对称性效应，有助于找到导致金融市场波动的原因，从而提出相应的对策来促进金融市场健康有序发展。

沪深300指数具有作为表征市场股票价格波动情况的功能，因此本文选择沪深300指数作为研究标的，利用GARCH和TGARCH模型来研究股票市场的波动情况，分析导致波动的原因，从而提出相应的对策来促进金融市场健康有序发展。

一、模型简介

1.ARMA模型

ARMA（p，q）模型的结构如下：

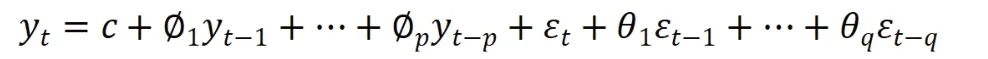
2.自回归条件异方差（ARCH）模型

自回归条件异方差（ARCH）模型是由均值方程和条件异方差方程组成的。ARCH（p）模型结构表示如下：

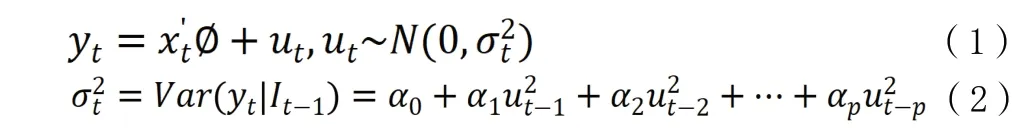
式（1）为均值方程，式（2）为条件异方差方程，p为ARCH模型的阶数，yt和x′t分别为被解释变量和解释变量，ut为无序列相关性的扰动项，为在t-1时刻时已知信息集It-1条件下的t时刻的扰动项的方差；α0为常数项，且α0＞0，αj≥0（j＝1，2，…，p）。

3. GARCH模型和TGARCH模型

GARCH模型的基本思想是：在ARCH模型的基础上，为了避免U2t滞后项过多，可采用加入σ2t的滞后项的方法，从而达到减少参数个数的目的。标准的GARCH（p，q）模型结构如下：

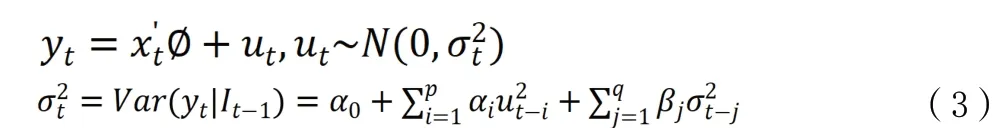
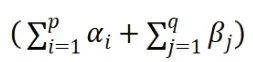
TGARCH模型又称作门限ARCH模型，这个模型通过一个虚拟变量协助刻画波动率的非对称性，TGARCH（1，1）模型结构如下：

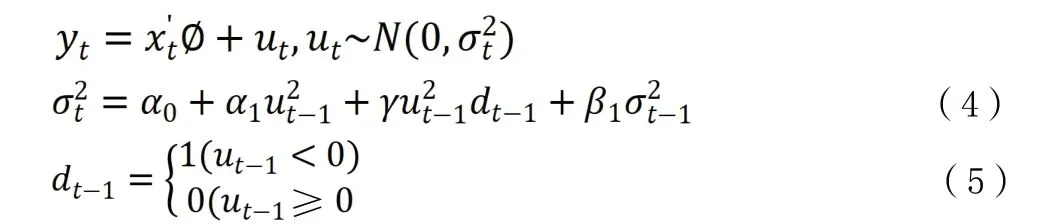
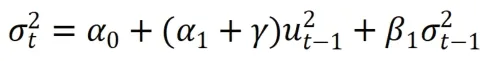
二、样本选取和数据预处理

本文选取2019年1月至2020年12月沪深300指数的日收盘价数据，所有的数据来源于网易财经。对沪深300指数的日收盘价数据取对数和一阶差分，即rt＝△lg(pt-1)，其中pt-1为前一天的收盘价格，rt为该指数在t时刻的对数收益率，得到相应的对数收益率时序数据。图2为该指数对应的对数收益率时序图。

从图2可得，该对数收益率序列没有明显的趋势特征，但具有集群效应，结合收盘价的时序图（图1）可以看出，在2019年，股市迎来了一波牛市，随后因为新冠疫情缘故影响国民经济的发展，迅速转为熊市，在防疫期间，国家出台许多有利于经济快速复苏的政策，在2020年下半年开始股市又经历一场增长较为迅速的牛市。

图1 工作日收盘价时序

图2 对数收益率时序

三、数据描述及分析

基于Eviews6.0软件，对该对数收益率序列进行描述性统计分析，结果如表1所示。从表1可得，该序列的中位数为0.001216大于均值0.001157，表明该序列右偏；该序列的偏度为-0.582520小于0，峰度约为8.4大于3，JB检验的P值远远小于0.01，说明该序列存在尖峰厚尾，不服从正态分布。

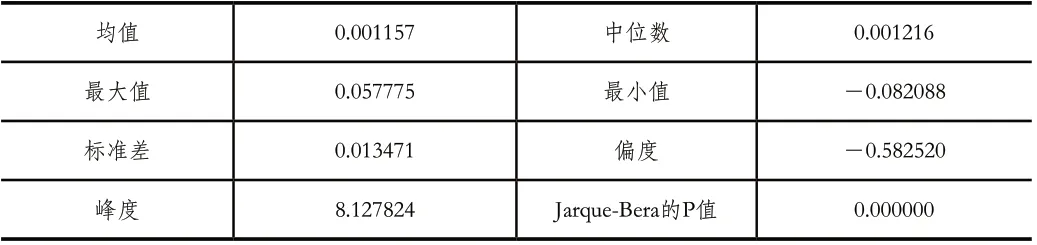
表1 沪深300指数收益率序列

利用ADF检验对对数收益率序列数据进行平稳性检验，ADF检验的P值小于0.05，由此可知对数收益率序列为平稳序列。

四、实证分析

1.模型的识别和定阶

基于上述ADF的检验结果，且发现该序列的自相关和偏自相关图都没有明显的拖尾和截尾现象，故尝试建立ARMA模型。

从自相关和偏自相关图发现ACF和PACF在三阶有略微显著的倾向，故判断AR过程和MA过程为1阶～3阶，利用Eviews6.0尝试将ARMA（p，q）中p，q阶分别历遍1-3阶，共6个模型。从模型估计结果看，ARMA（1，1）时AIC值最小，并且该模型中变量均显著，故确定模型为ARMA（1，1）模型。

2.ARCH效应检验

由上文可知，选择建立了ARMA（1，1）模型，然后利用ARCH-LM检验来检验该模型是否存在ARCH效应。如果该模型没有ARCH效应，说明ARMA（1，1）模型就已经足够刻画该对数收益率序列，否则我们考虑建立GARCH模型。由残差序列的自相关图（图3）可知，残差序列显示了较强的集群效应，因此对该残差序列进行了异方差检验即ARCH-LM检验，从检验结果可知，该序列具有较强的ARCH效应，因此我们选择GARCH模型进行建模分析是合理的。

图3 残差序列的自相关情况

3.GARCH模型

在研究金融时间序列时，常用的GARCH模型包括GARCH（1，1）、GARCH（1，2）、GARCH（2，1）、GARCH（2，2），在Eviews 6.0中对这4个模型分别建模，通过比较AIC确定最优模型。模型结果的AIC值如表2所示，其中GARCH（1，1）的AIC值最小，故选择GARCH（1，1）进行建模分析。

表2 GARCH模型的AIC值

在Eviews 6.0中对GARCH（1，1）进行统计回归，拟合后得到模型为：

GARCH（1，1）模型中的系数都是统计显著的，GARCH项系数与ARCH项系数之和等于0.965866小于1，满足模型参数约束条件，说明该模型能够很好的拟合数据，且这两项系数之和接近于1，说明了波动的持续性，可以有效地预测未来趋势，且对模型残差进行了异方差检验即ARCH-LM检验，ARCH-LM检验的P值0.05，因此残差序列不存在ARCH效应，即GARCH模型消除了残差序列异方差效应。

4.TGARCH模型

为了进一步研究沪深300指数对数收益率序列是否存在非对称性效应，建立TGARCH（1，1）模型对其进行分析研究。在Eviews 6.0中对TGARCH（1，1）进行统计回归，拟合后得到模型为：

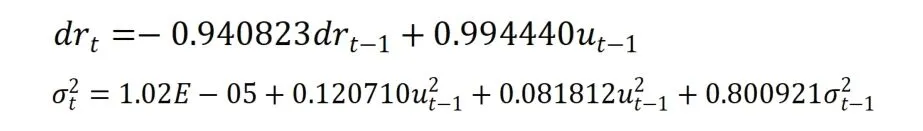
TGARCH（1，1）模型中常数项系数、ARCH系数和GARCH项系数的统计量P值均小于0.05即统计量均显著，表明该模型具有很好的拟合效果。从模型估计结果来看，γ的估计值为0.081812大于0，说明该序列存在非对称性效应。出现利好信息时有一个0.120710倍的冲击，而出现利空消息时会有一个0.202522（即0.081812＋0.120710）倍冲击，比较可得，负面冲击大于正面冲击的效果，即沪深300指数的对数收益率序列存在非对称性效应。

对模型残差进行了异方差检验即ARCH-LM检验，ARCH-LM检验的P值0.05，因此残差序列不存在ARCH效应，即TGARCH模型消除了残差序列异方差效应。

综上所述，TGARCH模型消除了残差序列异方差效应，沪深300指数的对数收益率序列存在非对称效应。

五、结论与建议

本文选取2019年1月2日～2020年12月31日沪深300指数日收盘价作为样本数据，基于Eviews 6.0建立ARMAGARCH模型对沪深300指数对数收益率序列进行实证分析，发现其对数收益率序列呈现出“尖峰厚尾”的特征，不服从正态分布，具有明显的波动集群性和ARCH效应，从TGARCH模型实证结果可以看出沪深300指数对数收益率存在非对称性效应，即利空消息对股市的波动影响大于利好消息对股市波动影响。

分析ARMA-GARCH模型结果发现，在2019年上半年、2020年3月份和2020年7月份这些时间段内对数收益率的波动性较大。2015年7月份证监会发布了大小限禁售令，股市跌入了熊市阶段。经过三年多的熊市阶段，在相关政策的刺激和利好消息的冲击下，2019年年初股市迎来一波牛市，2019年上半年对数收益率波动较大，2019年下半年对数收益率的波动相对较为平稳，在此期间，中国经济发展速度缓慢增长，金融市场不断完善。但是在2020年初突然爆发全球性的新冠疫情，经济发展受到疫情的冲击几乎处于全面停滞状态，股市急速下跌，2020年3月份沪深300指数对数收益率波动较大，此结果表明利空消息对股市波动的影响大于利好消息对股市波动的影响，与TGARCH模型的结果相吻合。在有效的抗疫和多项利好政策的支持下，经济开始缓慢回缓，股市开始小幅度上涨，2020年创业板改革并试点注册制和其他利好消息双重冲击下，7月股市大涨，迎来一波牛市，2020年7月份沪深300指数对数收益率波动相对较大。2020年尽管出台了多项利好政策但经济依然萎缩，股市却大涨，不难看出这是因为对金融市场的监管不够到位，有投资者投机取巧所导致的。

因此，建议做好信息披露，减少政府干预，增加市场信息的透明度；明确各个监管部门的权限和职责，能出台各项有利的措施来规范其行为，能避免资源的浪费，有效提高监管部门的工作效率；加强金融普法宣传，多种形式鼓励举报金融市场违法行为，发挥金融市场参与者的监督作用。总之从各个方面来完善我国金融市场的监管制度，加大监管力度，促进金融市场健康有序地发展。