适用于多直流馈入电网的频率弹性评估方法

刘阳，曹毅， 赵欣

(1. 国网江苏省电力有限公司，江苏 南京 210024；2. 东南大学电气工程学院，江苏 南京 210096)

0 引言

近年来，随着基于电网换相整流器技术(line-commutated converter，LCC)的特高压直流工程在我国陆续投运，区外来电已成为经济发达地区电网的主要区外电源[1—6]。特高压直流输电在远距离传输和隔离交流电网故障方面具有天然优势，为解决我国西部地区新能源外送和负荷中心电力紧缺问题提供了有效解决措施，但直流换相失败和闭锁等故障增加了电网运行的安全风险[7—11]。如何精准、定量地对多直流馈入电网的运行稳定性进行评估，已成为诸多学者研究的重点[12—13]。

经过多年研究，国内外学者提出了多种改善交直流混联电网频率稳定性的方法[14—16]。文献[17]提出多直流功率紧急支援协调控制技术，并以华东多直流馈入电网为例进行验证。文献[18]提出综合电网就地和远方信息的直流频率调制与紧急功率支援控制方案，改善电网频率稳定性。文献[19]为减小交流电网事故后的频率急剧下降和波动，提出用于互联交流电网的频率支援及恢复策略，保障电网在安全频率范围内运行并加速频率恢复速度。文献[20]提出交直流电网频率稳定紧急控制方法，通过三层向量机模型实现直流紧急功率支援和自动切负荷控制。现有电力系统稳定控制措施虽改善了交直流受端电网频率稳定性，但仍缺乏精准定量评估各措施作用效果的统一衡量指标。

弹性概念已被应用于环境学、经济学和生物学等学科中。对电力系统而言，弹性可用于评估电网对扰动的预防抵抗能力、故障过程中的吸收响应能力以及电网的快速恢复能力[21—24]。虽然电网弹性评估已取得一定进展，但交直流混联受端电网频率弹性精准评估目前尚处于起步阶段，缺乏成熟的研究成果。

综上所述，文中提出一种适用于多直流馈入电网的频率弹性评估方法，根据故障后电网频率变化特性，综合考虑直流闭锁损失的有功功率、发电机一次调频能力和负荷调频特性，精准评估受端电网的频率恢复能力以及各措施对电网频率稳定性提升的控制效果。

1 多直流馈入电网频率弹性评估模型

1.1 频率弹性评估指标

多直流馈入电网中，任一特高压直流闭锁后，典型电网频率变化曲线如图1所示。图中分为一次调频和二次调频阶段。一次调频由发电机的调速器完成，通常在8～15 s内结束；二次调频由自动发电控制(automatic generation control，AGC)实现，可使电网频率恢复至正常水平。由于故障后最低频率处通常采用一次调频，因此，文中所提频率弹性评估指标主要以一次调频阶段(故障后0～15 s)的频率变化情况为研究对象。

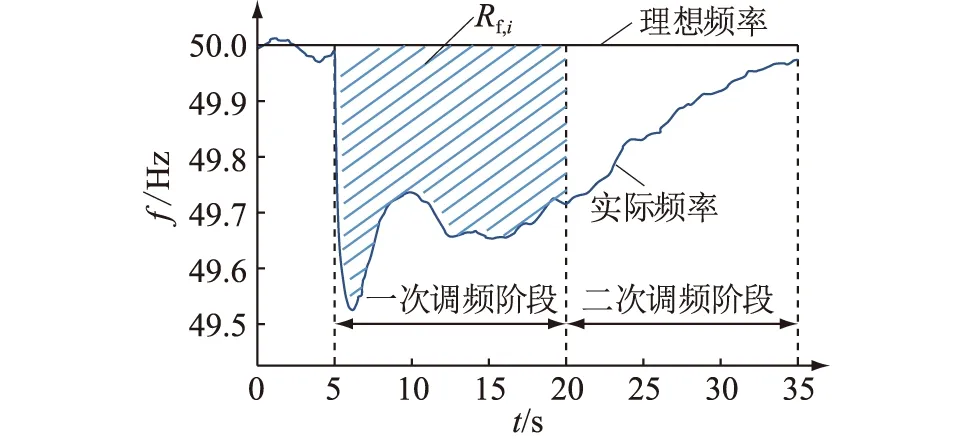
图1 直流闭锁后频率变化Fig.1 Frequency variation after direct current blocking

以直流闭锁后一次调频期间(0～15 s)实际频率与理想频率之间的面积为关键特征，提出频率弹性评估指标。

(1)

式中：Nhvdc为直流数量；Rf,i为直流i双极闭锁故障后，一次调频期间实际频率和理想频率之间的面积；ts为故障发生时刻；te为一次调频结束时刻；fs为理想频率曲线；fi为实际频率曲线。

对于任一直流双极闭锁故障，Rf,i越大，表明实际频率与理想频率越接近，电网的频率恢复力越强。由于电网存在多回直流，选择所有直流双极闭锁的Rf,i平均值作为电网的频率弹性评估指标，计算结果范围为(0,1]，数值越大，表明电网频率弹性越强。

1.2 频率弹性评估模型

为计算电网频率弹性评估指标，需建立相应的频率弹性评估数学模型。频率弹性评估目标函数如式(1)所示，约束条件主要包括交流电网潮流模型、特高压直流准稳态模型、电网机电暂态仿真方程。

1.2.1 交流电网潮流模型

交流电网的潮流方程为：

(2)

式中：节点功率方向以注入节点为正；ΔPi，ΔQi分别为节点i有功、无功功率偏差；PG,i，QG,i分别为节点i的发电机有功、无功功率；PL,i，QL,i分别为负荷有功、无功功率；Pd,i，Qd,i分别为交直流电网之间交换的有功和无功功率，整流侧取负，逆变侧取正；Gi,j，Bi,j为交流电网导纳矩阵元素；Ui，θi分别为节点i的电压幅值和相角；n为节点数量。

1.2.2 特高压直流准稳态模型

以图2所示双端直流系统为例，直流输电的潮流模型如式(3)—式(7)所示。

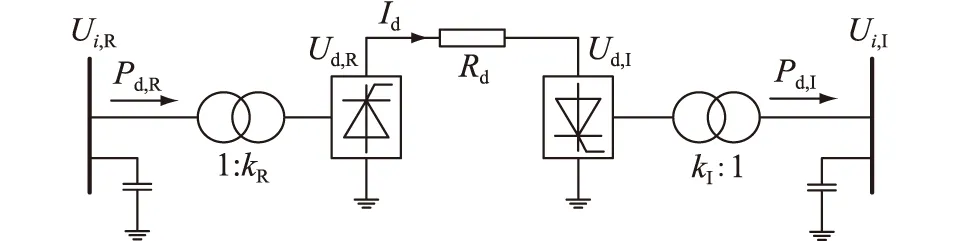
图2 双端直流系统模型Fig.2 Model of two-terminal direct current system

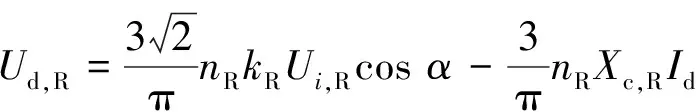
(3)

(4)

Pd,R=Ud,RId

(5)

Pd,I=Ud,IId

(6)

Ud,R=Ud,I+RdId

(7)

式中：下标R和I分别表示整流侧和逆变侧;Ud为直流电压；Ui为交流母线电压；n为桥数；k为换流变压器变比；α为整流侧触发角；γ为逆变侧熄弧角；Xc为等效换相电抗；Id为直流线路电流；Pd为直流有功功率。

1.2.3 电网机电暂态仿真方程

交直流混联电网的机电暂态方程为：

(8)

(9)

1.3 频率弹性评估流程

式(1)—式(9)组成了交直流混联电网的频率弹性评估模型，涉及多回直流分别发生闭锁后频率变化曲线特征提取以及频率弹性指标计算，具体评估流程如图3所示。

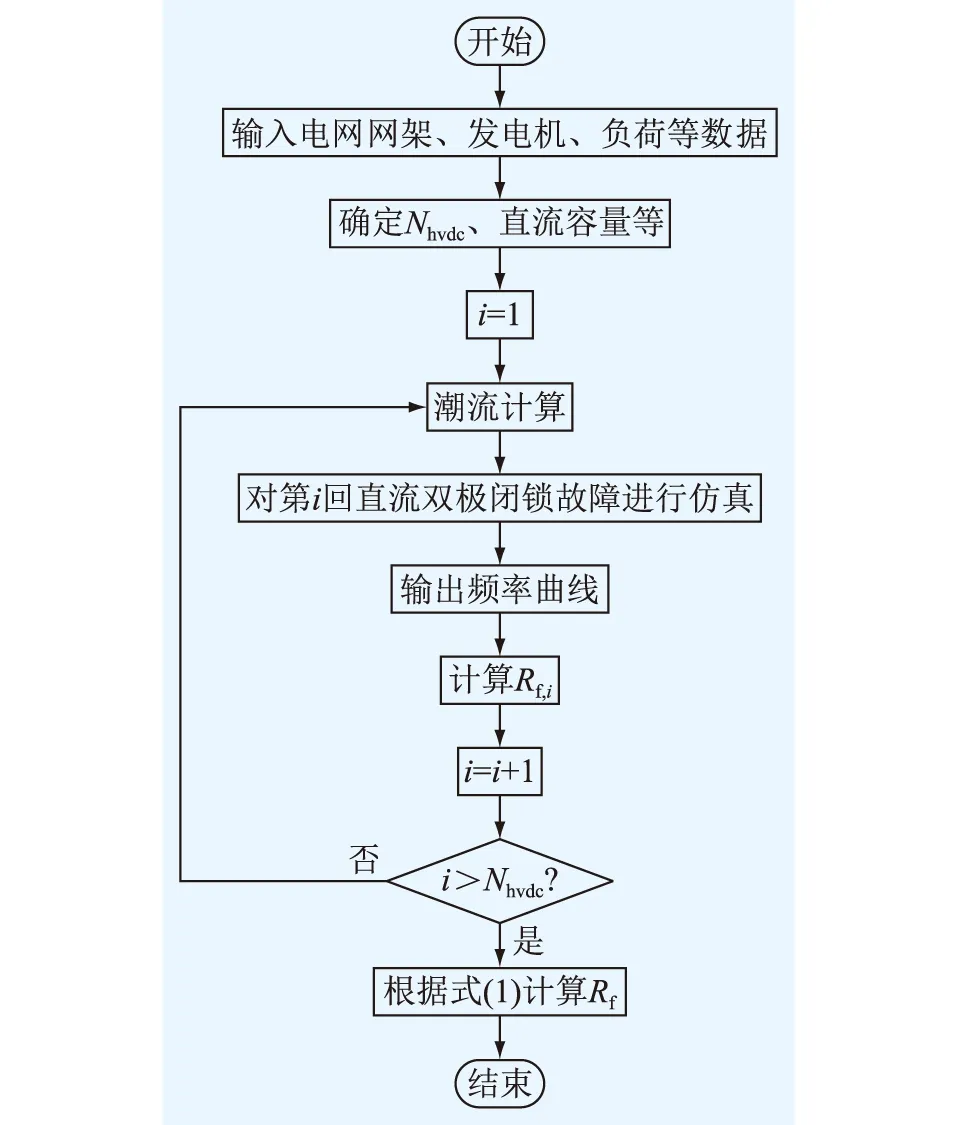
图3 频率弹性评估流程Fig.3 The flow of frequency resilience evaluation

2 频率弹性评估方法在电网中的应用分析

为了验证所提电力系统频率弹性指标的有效性，以华东电网为例进行仿真计算。华东电网是我国电网的重要组成部分，属于典型多直流馈入受端电网，主要包括锦苏、雁淮、锡泰、宾金和复奉五大特高压直流。特高压直流给华东电网提供大量区外来电的同时，直流闭锁故障也带来了电网频率稳定隐患。以某年汛期低谷运行方式为例，所有特高压直流输送功率、电压等级信息如表1所示。

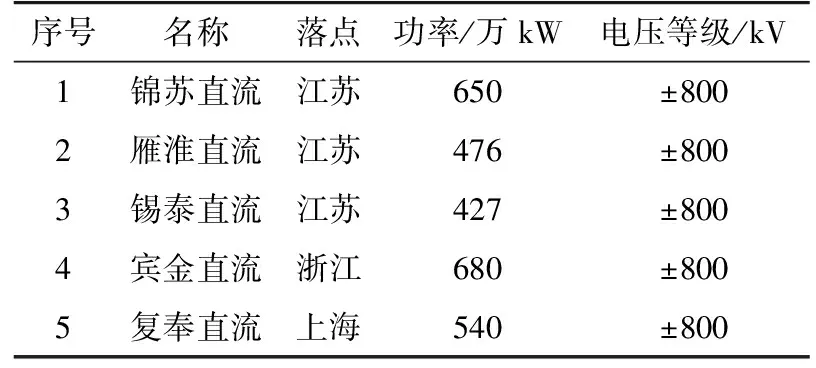
表1 华东电网特高压直流信息Table 1 The ultra high voltage direct current data of East China power grid

仿真采用Matlab完成整体框架编程，并调用BPA进行潮流计算和机电暂态仿真。

2.1 电网频率弹性评估计算

根据仿真结果，锦苏等五回特高压直流闭锁后的电网最低频率变化曲线如图4所示。需要注意的是，弹性指标只需一次调频阶段的频率变化数据，为提升计算效率，BPA暂态仿真未考虑二次调频，因此，二次调频阶段的频率曲线与实际变化存在差异，但不影响计算结果。

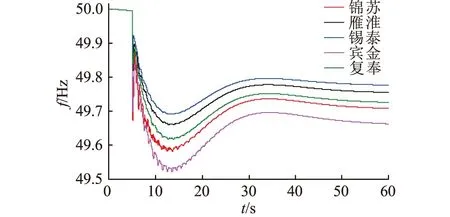
图4 不同直流闭锁后的频率变化Fig.4 Frequency variation after different direct current blocked faults

根据式(1)计算得到不同直流闭锁后的Rf,i，如图5所示。分析可知，由于电网一次调频能力不变，直流闭锁后的Rf,i与特高压直流输送功率的大小相关，直流功率越大，Rf,i越小，表明故障后频率恢复速度越慢；反之，则故障后频率恢复速度越快。计算可得，华东电网汛低运行方式下的Rf为0.702。

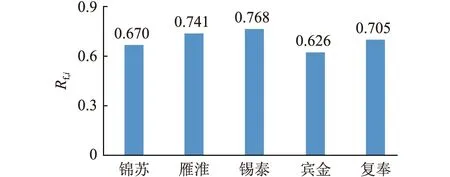
图5 不同直流闭锁后的Rf,iFig.5 Rf,i after different direct current blocking faults

2.2 不同控制措施提升电网频率弹性效果对比

基于文中电网频率弹性评估指标，对表2中常见电网控制措施提升电网弹性的效果进行对比分析。

表2 频率稳定性提升措施Table 2 Frequency stability improvement methods

华东电网汛低运行方式下，发生直流闭锁后，采用措施1～3前后频率弹性指标变化如表3所示。

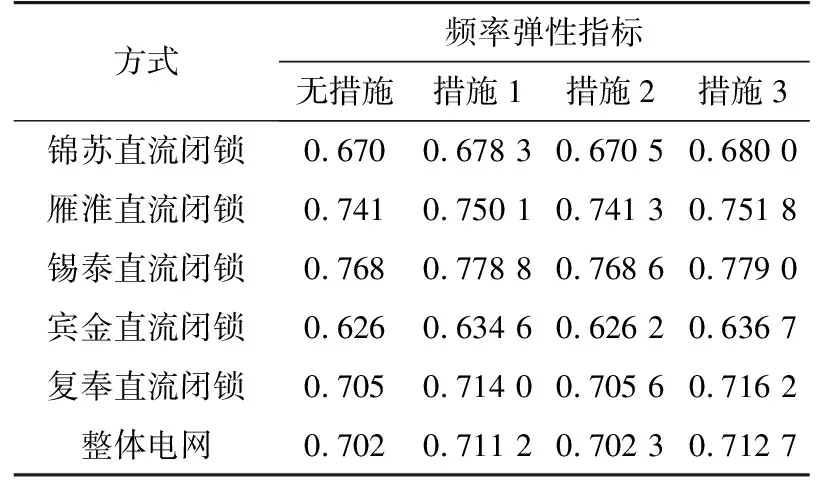
表3 采用措施1～3前后的频率弹性指标对比Table 3 Comparison of frequency resilience index before and after taking measure 1～3

由表3可知，采用措施1～3后,Rf分别提升了0.009 2，0.000 3，0.010 7。可见，发生直流闭锁后，采用措施1～3可有效提升电网频率恢复速度、电网频率弹性及稳定性。且3种措施中，负荷快速控制措施提升电网弹性效果最好，风电参与一次调频次之，增加发电机效率再次之。实际电网运行中，建议深度挖掘电网可控负荷资源，以较小的成本有效提升电网频率弹性，加快故障后电网频率恢复速度。文中频率弹性评估指标可实现不同频率控制措施对于电网稳定性作用的精准定量对比计算，计算结果可用于实际电网的规划运行。

3 结论

随着我国特高压直流工程的不断建成投运，交直流混联特征日趋突显，直流闭锁后电网损失较大的有功功率，导致低频问题突出，给电网的安全稳定运行带来隐患。根据电网运行特性，合理精准评估多直流馈入电网遭受故障后的恢复能力，对于电网的规划运行有着重要的指导意义。

文中提出的适用于多直流馈入电网的频率弹性评估指标及方法，综合直流闭锁故障后的最低频率及频率恢复速度，实现了受端电网频率弹性的精确量化评估。以包含多回直流馈入的华东电网为例，对典型电网控制措施改善电网频率稳定性的有效性进行定量对比分析，结果表明风电一次调频、增加燃机、负荷快速控制等措施可有效提升电网频率恢复能力。其中，挖掘电网可控负荷资源可有效提升电网频率稳定性，为交直流混联受端电网的安全稳定运行提供有效保障。