基于FCM和DTW的多分区电压支撑能力评估

徐贤， 管益斌， 周挺， 赵香， 张重阳， 柳伟

(1. 国网江苏省电力有限公司，江苏 南京 210024；2. 南京理工大学自动化学院，江苏 南京 210094)

0 引言

随着现代用电需求的日益增长，电网规模在不断扩大，电网的无功优化控制也日渐复杂。自动电压控制(automatic voltage control,AVC)系统从全局角度对广域分散的无功源及无功补偿装置进行协调优化控制[1—4]。然而，AVC调控系统控制周期较长，一般为分钟级，且全网无功调节后还可能存在分区无功不平衡的问题。为了便于AVC系统更好地进行无功协调控制，为其从全局角度调整参数、进行控制策略优化以及补偿装置配置提供依据，亟需对电网多分区电压支撑能力进行实时准确的评估。

现有研究在评估指标体系、评估方法等方面作出了巨大贡献。文献[5]从配置、维护、运行3个角度构建了完备的评估指标体系，对城市配电网的无功运行现状进行了科学实用的评估；文献[6]结合静态能量函数，以电压稳定为基础，对区域电网无功能力进行了评价；文献[7—8]从电压考核标准、无功容量、无功协调控制3个角度进行无功电压指标体系的构建，并对各指标进行权重赋值和计算方法的研究。

电网无功电压、负荷实时需求等是随时波动的，而AVC不同层级的轮控周期不同，因此将某一个时间断面的电力信息作为控制依据不够客观。文献[9]采用模糊聚类法对电压薄弱节点进行模糊分割，确定无功补偿的具体个数及相应地点，但需要主观确定阀值λ，并多次用方差比率检验分类是否合理。文献[10—12]介绍了模糊C均值聚类(fuzzy C-means algorithm，FCM)在负荷预测、风险预警以及配电网动态重构等方面的应用，通过优化目标函数对电网大量数据进行模糊聚类，并提取平均特征。文献[13—14]将动态时间归整算法(dy na mic time warping，DTW)运用于电能质量的综合评估与分级评估，利用其能够匹配长短不一的2个序列的特点，解决实际电网数据有缺失的问题，能够更准确地评估实际电网的运行状态。

鉴于上述分析，文中根据电网分层分区架构和AVC无功协调控制特点，建立了一套能够从多角度表征分区电压支撑能力的指标体系，并结合FCM处理电网大数据量的特点和DTW对序列模式匹配的特点，对电网多分区电压支撑能力进行评估，解决电网数据波动对评估产生的影响。最后，以某典型电网为例，将文中方法与单独DTW算法评估进行了仿真对比，验证所提方法的优势。

1 电网分区电压支撑能力评估指标体系

1.1 主网分区电压裕度指标

电压质量是衡量电力系统稳定状态的重要指标。电网中节点电压接近电压崩溃点时，系统维持稳定的电压可调裕度较低[15—16]。因此，制定电压裕度指标评估电压支撑能力，指标公式如式(1)所示。为了简化计算并使序列便于模式匹配，文中在制定指标体系的同时均作了归一化处理。

(1)

其中：

(2)

式中：N为分区节点数量；Ui为第i个节点的电压；Ui,cr为第i个节点在电压崩溃时的临界安全电压。

1.2 输电断面功率传输能力指标

(3)

(4)

式中：Ip为输电断面功率传输能力指标；Ptr为电力系统监控采取的一个潮流输电断面的功率传输能力；Nsel为采取的一个分区的潮流输电断面数；Pmax为当前无功状态下输电断面功率传输极限；Pcut为采取的输电断面功率值；λ为约束因子，目的是优化对数据的归一化处理，避免计算机对微小数据识别错误，因此λ一般取0～1的数值，文中取0.2。

1.3 分区无功裕度指标

无功补偿遵循就地平衡的原则，分区内发电机作为主要的无功电源，其正常运行和进相运行时发出或吸收无功对系统电压、无功状态都有着决定性的作用。分区内各种无功补偿设备补偿无功，分区间联络线互为无功备用[16]。定义分区的无功能力为：在系统稳定的前提下，所有无功电源能够提供的无功。建立分区无功裕度指标如下[17]：

(5)

式中：QB为分区实时无功容量；Qg,Gmax为第g个发电厂机组正常运行或进相运行时可以调节的最大无功；Qj,rec为第j个无功补偿装置的容量(包括电容器、电抗器、SVC/SVG等)；Ql,Pmax为第l个互联分区可以提供的最大无功；NG，Nr，Np分别为分区内发电厂机组数、无功补偿装置数、互联分区数。

1.4 分区无功偏差裕度指标

AVC系统包括逐级的主系统和子系统，在调节时，各级会通过控制指令来控制相应的子系统[2]。无功偏差裕度定义为当前分区无功总容量与省调AVC系统下发的控制指令的无功目标之差，分区无功偏差裕度指标归一化后公式如下：

(6)

式中：QAVC为上一级AVC系统根据全局无功调控所制定的该分区无功；QA为分区所提供的无功总容量。

上述指标从不同角度表征分区电压支撑能力，各指标的重要性有所不同，因此文中在具体算例中列出了所有指标各等级的参考值，采用DTW算法将这些参考值组成的参考样本序列与待评估样本序列进行模式匹配。

2 电网分区电压支撑能力评估方法

利用FCM对电网多个分区的不同时间断面的数据进行聚类，得到聚类中心和隶属度矩阵。DTW计算参考样本和聚类中心的相似度。通过对聚类中心数据的电压支撑能力进行评估，进而确定该类分区的电压支撑能力。

根据上述指标体系提取电网分区的各指标数据，建立指标样本集X=(x1,x2,…,xk,…,xn),是一个4行n列的矩阵，其中xk=(xk1,xk2,xk3,xk4)T表示各个分区的指标数据向量，k=1,2,…,n，在聚类过程中，以各向量之间的欧式距离作为聚类依据，并不断调整聚类中心，具体算法过程如下。

2.1 FCM聚类过程

电网分区电压支撑能力的强弱取决于该分区各种无功补偿设备的配置、容量以及分区实际所需容量。由于电网中负荷是随时波动的，因此分区电压支撑能力是一个没有明确界限的概念。因此，采用模糊理论对这一问题进行分析能够达到更好的效果。FCM以式(9)为约束，以式(7)为目标函数，优化获取每个样本对各个聚类中心的隶属度，并对比分析所求隶属度大小，自动对电网多个分区的不同时间断面的电压支撑能力指标数据进行模糊聚类，以聚类中心的指标数据作为待评估数据，避免电网中数据波动对分析结果产生影响。具体流程如图1所示。

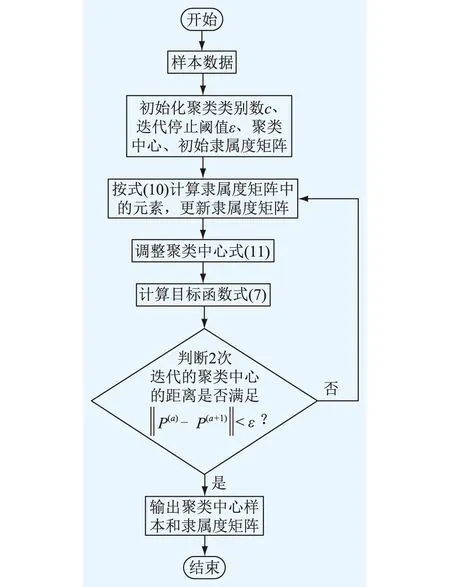
图1 模糊C均值聚类算法流程Fig.1 Flow chart of fuzzy C-means clustering algorithm

2.1.1 模糊聚类的目标函数

模糊聚类的目标函数：

(7)

式中：c为聚类类别数；n为分区个数，2≤c≤n；U=[uik]c×n为隶属度矩阵，其元素uik为第k个样本对第i类的隶属度；pi(i=1,2,…,c)为第i类的聚类中心，是由上文阐述的4个指标数据构成的四维向量；m为加权指数，此处取经验值2；dik为第k个样本与聚类中心pi之间的欧式距离，即按式(8)计算。

dik=‖xk-pi‖

(8)

2.1.2 约束条件

每个样本对于各个类的隶属度之和为1，即应满足下式：

(9)

2.1.3 算法的迭代过程

初始化算法所用到的参数：设定聚类类别数c为参考样本个数；初始聚类中心P(0)，该算法的初始聚类中心可随机选取，不影响聚类结果；初始隶属度矩阵U(0)，由约束条件可知，隶属度矩阵每一列的值之和为1；设置合理的迭代停止阈值ε；初始迭代系数a，可反映算法迭代次数。

(1) 按式(10)计算隶属度矩阵中的元素，更新隶属度矩阵。

(10)

(2) 按式(11)计算聚类中心向量的元素，调整聚类中心：

(11)

(3) 求解目标函数，即式(7)。

(4) 迭代判断。若║P(a)-P(a+1)║<ε，则迭代停止；否则，迭代次数a=a+1，转入(2)计算。

2.2 DTW算法

DTW算法[19—21]对聚类中心样本数据序列与各个参考数据序列进行模式识别，计算出最优动态归整路径的距离，距离越小，相似度越高，从而确定与聚类中心样本数据最相似的参考数据，以此来评估一类分区的电压支撑能力。

2.2.1 距离矩阵

计算待评估聚类中心序列与参考序列各元素之间的距离形成距离矩阵。假设某聚类中心样本序列和某参考序列分别为Z=(z1,z2,…,zm),Y=(y1,y2,…,yn)，2个序列中所有点的距离用矩阵dΔ表示：

(12)

式中：dij为长度为m的待评估序列的第i个元素与长度为n的参考序列的第j个元素的欧式距离。

2.2.2 最优动态路径规划

首先，用一个向量W=(w1,…,wk,…,wR)表示动态归整路径，并建立一个映射关系：

wk=dij

(13)

向量W的长度满足式(14):

max(m,n)≤R≤m+n-1

(14)

由于要比较的2个序列本身有一定的对应关系，所以不需要对每个路径都计算累加距离。为提高算法收敛速度，更快找到最优动态路径，设定必须满足的3个约束条件。

(1) 边界条件。由于要比较的2个序列元素排列顺序是固有的，且2个序列的元素有一定的对应关系，所以动态路径归整必须从元素(z1,y1)开始，到元素(zm,yn)结束。

(2) 单调性。比较2个序列时，需要按一个方向的单调比较，不可以有重复比较。即：对于wk=dij，wk+1=dst，应满足式(15)。

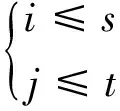
(15)

(3) 连续性。动态规划路径中2个点的距离必须是相邻2个点的距离，不可以有跨越点的交叉比较。即：对于wk=dij，wk+1=dst，应满足式(16)。

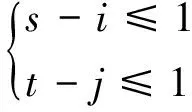
(16)

2.2.3 最小归整距离

最小归整距离为最优动态归整路径的累加距离D(i,j)，在满足3个约束条件的前提下可得：

(17)

由式(17)可以得到待评估聚类中心数据与各参考样本数据的最小归整距离。

3 案例分析

图2为区域电网主网架构，A、B、C、D、E分区电网通过双线与主网相连。采取各分区的10个时间断面的数据进行评估方法验证。表1为各分区第一个时间断面样本数据，其余时间断面的数据未展示。表2为参考样本数据，参考样本b1、b2、b3、b4、b5的电压支撑能力等级分别为强、较强、一般、较弱、弱。

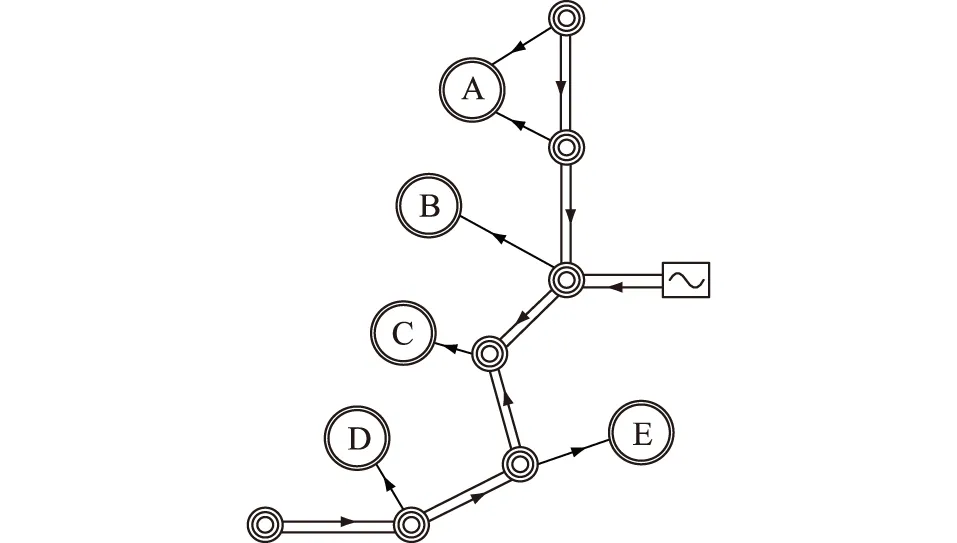
图2 区域电网主网架构Fig.2 Layout of the main grid structure of the regional power grid

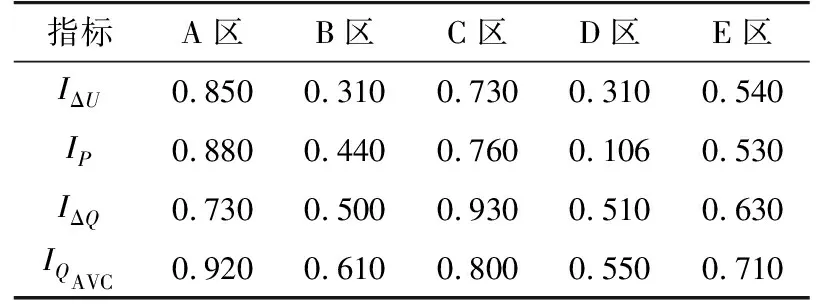
表1 各分区第一个时间断面的样本数据Table 1 Sample data of the first time section of each partition

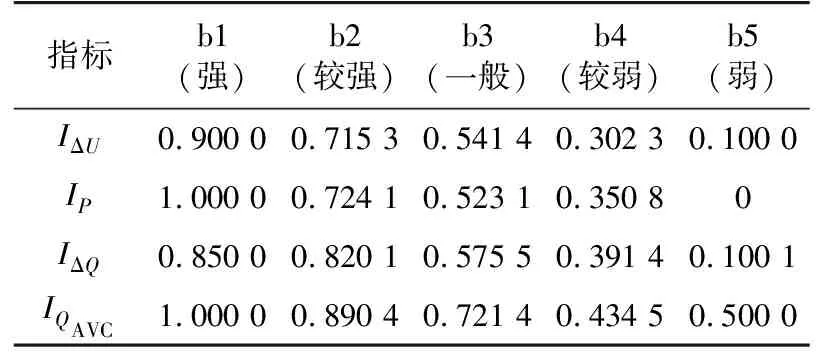
表2 参考样本数据及其电压支撑能力等级Table 2 Reference sample data and its voltage support capability level

运用FCM对5个分区10个时间断面的指标数据进行模糊聚类，可得到聚类中心样本数据。文中将数据聚类为5类，即参考样本的样本数目，各聚类中心数据见表3。各样本关于各聚类中心的隶属度大小表示样本与各聚类中心的隶属关系。为了更加直观、快速地确定与样本隶属度最高的聚类中心，采用origin软件绘制3D条形图来展示，见图3。

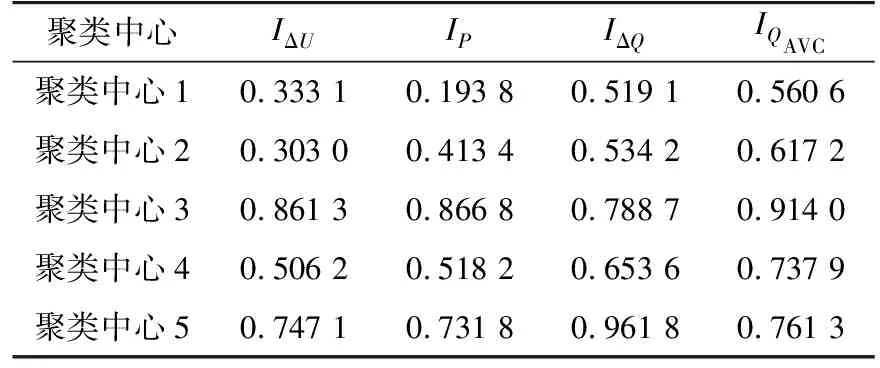
表3 分区样本聚类中心数据Table 3 Clustering center data of partitioned samples

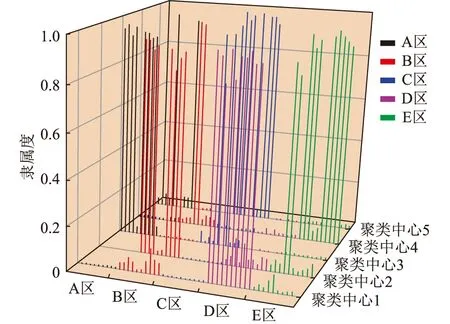
图3 待评估样本关于各聚类中心隶属度Fig.3 The membership degree of each cluster center of the sample to be evaluated

其中，各分区的10个断面的指标数据对于各聚类中心的隶属度用不同颜色表示。以图中A区为例，同一个时间断面与5个聚类中心的隶属度之间进行比较，A区10个断面数据中有2个断面的数据与聚类中心5的隶属度最高，但是其余时间断面的数据与聚类中心3的隶属度最高，因此以聚类中心3代表A区样本数据。同理，聚类中心5代表C区样本，聚类中心2代表B区样本，聚类中心4代表E区样本，聚类中心1代表D区样本。

各聚类中心与各参考样本的最小归整距离如图4所示。以聚类中心1为例，聚类中心1与参考样本b4的最小归整距离最小，则聚类中心1的电压支撑能力等级为较弱，而由前述分析可知聚类中心1可以代表D分区的样本特征，因此可得D区的电压支撑能力较弱。同理可以分析得到其他聚类中心与参考样本的相似关系以及各分区的电压支撑能力等级，如图5所示。A区、B区、C区、D区、E区的电压支撑能力分别为强、较弱、较强、较弱、一般。

图4 各聚类中心样本与参考样本的最小归整距离Fig.4 The minimum warping distance between each cluster center sample and reference sample

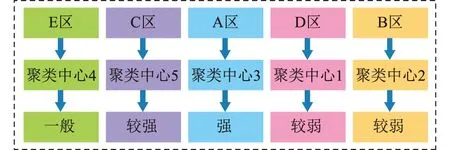
图5 各分区与聚类中心的隶属关系以及评估结果Fig.5 The relation diagram between each partitionand clustering center and reference sample

表4为直接用DTW计算的C分区10个时间断面的样本与各参考样本的最小归整距离。图6展示了C分区的T1和T72个时间断面的数据与各参考样本的最小归整距离，其中T5与T7时刻的各最小归整距离趋势相同，其余时刻与T1时刻的最小归整距离趋势相同。从图6可以看出T1时刻的样本与参考样本b3相似度最高，所以T1时刻的电压支撑能力等级为一般，而T7时刻的样本与参考样本b2相似度最高，故其电压支撑能力等级为较强。由此可得，在一个轮控周期内，同一个分区不同时刻的电压支撑能力等级可能不同。基于FCM与DTW的电压支撑能力评估方法提取聚类中心，代表该类中分区的所有时间断面的样本平均特征，可以更加客观地评估分区的电压支撑能力，同时避免因少许波动数据影响评估结果。

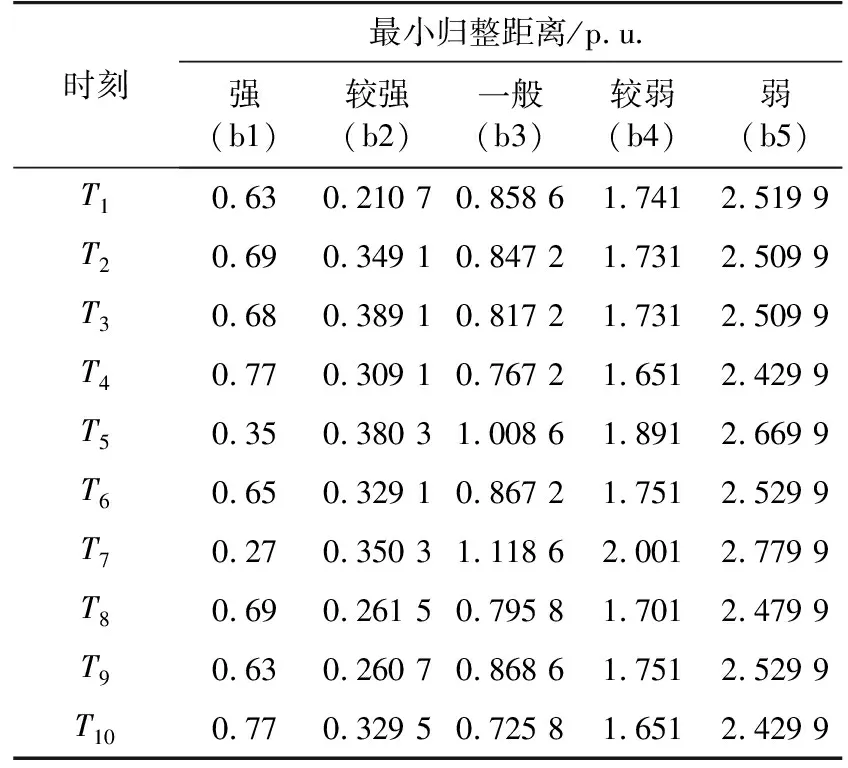
表4 C分区样本与各参考样本的最小归整距离Table 4 The minimum warping distance between the C partition sample and each reference sample

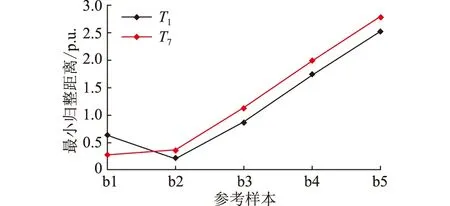
图6 C分区T1和T7时刻样本与各参考样本的最小归整距离Fig.6 The minimum warping distance between samples and reference samples at time T1 and time T7 in partition C

4 结语

文中通过FCM对多个分区的多个时间断面的电压支撑能力指标数据进行聚类，利用其收敛速度快且能处理大数据量的特点，同时评估多个分区多个时间断面的分区电压支撑能力。采用DTW评估聚类中心与参考样本的相似度，进而评估各类分区的电压支撑能力。解决了分区无功电压大数据量处理和波动性的问题，能够为AVC系统全局无功电压控制提供数据支撑，有利于层级间的协调控制。另外，对于多分区的电网可以通过聚类的方法较快地评估出电网无功较弱的几个分区，再通过隶属度溯源电压支撑能力最弱的分区，为AVC系统提供数据支撑和决策依据。

本文得到国网江苏省电力有限公司科技项目(J2019031)资助，谨此致谢！