基于半动态拓扑优化的电网运行方式辅助决策

翁毅选， 马伟哲， 史军， 何晓峰， 翟鹤峰， 赵利刚

(1. 深圳供电局有限公司，广东 深圳，518001；2. 直流输电技术国家重点实验室(南方电网科学研究院有限责任公司)，广东 广州，510663)

0 引言

传统电力系统运行中，配电网可通过重构改变运行的拓扑结构[1—3]，而输电网的拓扑结构除了线路检修或偶发故障外，通常认为是固定不变的，不考虑其拓扑随系统运行方式改变而灵活调整。但实际上，输电网结构是在规划时考虑的典型或极限运行方式下确定的，留有较大安全裕度[4—5]。而实际系统运行中负荷水平是变化的，因此对于多数运行方式，在不影响电网运行安全性的前提下，可以进一步考虑对网络拓扑进行优化，从而自适应跟踪实际系统负荷变化，提升运行经济性。

输电网拓扑优化问题[6—9]是对电网运行过程中的网络结构进行动态调整，灵活地选择最优的网络运行拓扑，以改善电网运行中存在的输电阻塞[10—11]、短路电流超标[12]、电压越限[13]等问题。实际系统运行中，调度人员可以改变网络运行拓扑，如春节期间调压困难时会断开部分线路使其处于热备用，从而降低站点电压。近年来，网络拓扑优化问题引起了国内外专家学者的广泛关注和探索研究，诸多研究表明在电力系统运行中根据电网的实际状况和需求灵活地改变网络拓扑，将有助于进一步提升系统运行的安全经济性能[14—16]，文献[17]也对实施网络拓扑优化的可行性进行了论述。

文献[18]对电网结构优化问题进行了综述，当前网络拓扑优化方法可分为2类：一类是静态网络拓扑优化，即不考虑网络结构随时间的变化而变化。文献[6]首次提出输电网结构优化的混合整数线性规划(mixed integer linear programming，MILP)模型；文献[10]采用网络拓扑优化进行电网安全均匀调度，改善潮流分布的均匀度；文献[16]在进行网络拓扑优化建模时考虑N-1安全约束，从而提升对系统安全性的考虑。静态网络拓扑优化方法的优势在于表征线路开断与否的状态变量与时间无关，因此计算效率较高，但缺点在于不能动态跟踪负荷变化，灵活调整网络结构。

另一类是动态网络拓扑优化，即考虑网络结构随时间变化而动态变化。文献[19]考虑网络拓扑优化用于电力市场出清，并指出该方法可提高市场出清效率；文献[20]考虑网络拓扑优化用于机组组合，并指出该方法可以显著节省运行成本。文献[21]则同时考虑网络拓扑优化与N-1约束构建机组组合模型。动态网络拓扑优化方法的优点在于网络拓扑随时间的变化自适应地动态调整，系统运行灵活性好，但缺点在于表征线路开断与否的状态变量与时间关联，计算难度大，计算效率低。

综上，为优化电网运行方式，兼顾模型解算效率与运行灵活性，提出半动态拓扑优化方法，进而构建一般形式的电网运行方式辅助决策模型。最后，通过算例分析说明了该优化方法的优势。

1 网络拓扑优化方法

1.1 现有网络拓扑优化方法

文中从优化考虑的线路状态变量与时间的关联关系角度，将现有网络拓扑优化方法分为静态拓扑优化与动态拓扑优化2类。其中，静态拓扑优化的特点在于优化网络结构时不考虑随时间变化，该类方法对应的拓扑约束为[3]：

(1)

式中：L为线路集合；C为最大允许断开的线路数；zij为表示线路(i,j)断开与闭合的0-1变量，若断开则为0，闭合则为1。

由于该类方法的网络拓扑变化与时间无关，因此不能动态跟踪负荷与发电，优化所得结果的运行灵活性较差。

动态拓扑优化的特点在于考虑每条线路断开与否与时间关联，但各时段间断开与否无耦合关系，该类方法对应的拓扑约束为[15]：

(2)

式中：T为表征时间周期的集合；zij,t为表示线路(i,j)在时段t断开与否的0-1变量，若在时段t断开则为0，闭合则为1。

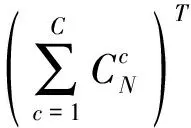
1.2 半动态网络拓扑优化方法

针对上述静态与动态网络拓扑优化方法存在的缺点，文中借鉴文献[22]所提配电网重构方案思路，即考虑线路在一天内仅进行一次状态切换，第二日优化则在前一日的拓扑基础上再次进行优化，提出了一种半动态网络拓扑优化方法，该类方法对应的拓扑约束可用式(3)表示。

(3)

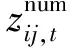
在计算效率方面，文中所提半动态拓扑优化方法的特点在于对系统中的每一条线路，在优化的整个时间周期内仅能改变状态一次，即假设初始状态下所有线路闭合，一旦线路某一时段断开，则在之后剩余的时间段内均保持断开状态不变。因此，由式(3)可知，对包含N条线路，T个时段的运行方式优化问题而言，该类网络拓扑优化方法最大将存在与动态拓扑优化方法相同的线路组合方式，最少将存在与静态拓扑优化方法相同的线路组合方式，即组合方式介于静态方法与动态方法之间，因而具有模型求解计算上的优势。

在系统运行灵活性方面，半动态拓扑优化方法可以在某一关键时段切换线路状态，并保持后续线路状态不变，因此也具有一定的运行灵活性。此外，对运行管理人员来说，每天只需要根据日前决策的线路开断结果对线路开关操作一次，操作简便；同时，对线路开关而言，不会像动态方法那样造成线路开关频繁动作，因此有利于延长开关使用寿命。

另外，需要说明的是文中所做的初始状态下所有线路均闭合的假设并不影响模型的适用性，对于实际中不能参与开断的线路或者处于检修状态已断开的线路只需要固定其对应的线路状态变量为1或0即可。为更好地说明3类网络拓扑优化方法的区别，图1给出了3类方法对应的线路状态变量z的可取值示意，可以更加直观地看出3类方法在变量数目和组合方式上的差异。

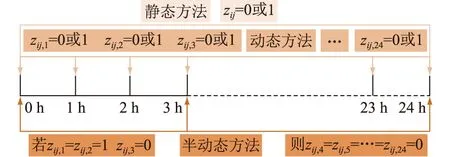
图1 3类网络拓扑优化方法对应的线路状态变量Fig.1 Schematic of line state variables corresponding tothree types of network topology optimization methods

2 基于拓扑优化的电网运行方式辅助决策

基于上章所提网络拓扑优化方法，以电力系统日前运行方式辅助决策问题为例，计及网络拓扑优化构建一般形式的电网运行方式辅助决策模型。其中，目标函数为日前所有发电机组的发电出力成本最小；约束主要包括机组出力范围约束、爬坡速率约束、潮流约束、传输功率约束、备用约束以及上节所述网络拓扑约束。

2.1 目标函数

(4)

式中：G为发电机集合；ag，bg，cg分别为机组g发电成本函数的二次、一次和常数项；Pg,t为机组g在时段t的有功输出功率。式(4)所示目标函数即为发电机组有功出力对应的二次成本函数，即最小化整个系统的发电成本。

2.2 约束条件

(1) 机组出力上、下限约束。

(5)

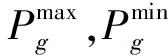
(2) 机组爬坡速率约束。

(6)

(7)

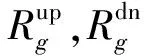
(3) 线路传输容量约束。

(θi,t-θj,t)/xij-fij,t+(1-z)M≥0
∀(i,j)∈L,t∈T

(8)

(θi,t-θj,t)/xij-fij,t-(1-z)M≤0
∀(i,j)∈L,t∈T

(9)

(10)

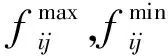
(4) 节点相角约束。

(11)

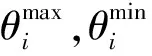
(5) 节点功率平衡约束。

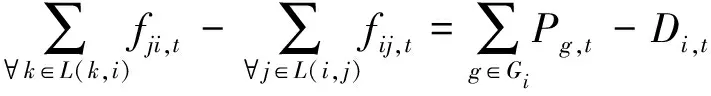
(12)

式中：Di,t为节点i在时段t的负荷量；对线路(k,i)，k∈L(k,i)表示与节点i相连且末端节点为i的线路构成的集合；同理，j∈L(i,j)表示与节点i相连且始端节点为i的线路构成的集合。

(6) 备用约束。文中在进行运行方式辅助优化时仅考虑系统正常运行所需要的旋转备用，以应对负荷及新能源出力波动带来的影响，暂不考虑偶发故障所需的事故备用约束。

(13)

(14)

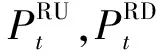
(7) 网络拓扑约束。即式(1)或式(2)或式(3)约束。采用不同的网络拓扑优化方法，需选择相对应的约束式。

易知，上述基于网络拓扑优化的电力系统日前运行方式辅助决策模型除了目标函数为二次函数外，约束条件均为线性，属于混合整数二次规划问题，虽然现有求解器也可直接对此类问题进行求解，但计算效率相对较低，因此下节将介绍线性化方法将目标函数线性化，从而将模型转化为MILP模型进行求解。

3 模型转化与求解

机组的发电成本为二次函数，为减轻模型求解难度，将其采用插值线性化方法[23]线性近似表示。

(15)

上述线性近似方法须同时满足以下约束条件：

(16)

(17)

(18)

(19)

(20)

易知，通过上述转化，文中基于网络拓扑优化的电力系统运行方式辅助决策模型已转化为MILP模型。

此外，考虑到应用于实际大系统时，现有求解器直接求解大规模MILP问题仍存在效率低下的问题，文中提出采用Benders分解法求解大规模算例系统。Benders分解法的实质是将一个大规模但仅需求解一次的问题，分解成一系列的小问题反复迭代求解的方法，其示意如图2所示。

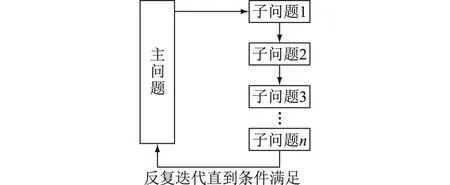
图2 Benders分解法示意Fig.2 Schematic diagram of Benders decomposition

将上述MILP问题表示为矩阵的一般形式为：

(21)

式中：y为表征模型中0-1变量相关的变量；x为表征模型中连续变量相关的变量；A，B为约束中相关的系数；c,f为目标函数中的相关系数。

(22)

式中：p为引入的对偶变量。

当求解子问题后，根据判断结果添加约束至主问题进行求解再次得到新的0-1变量y。然后反复迭代求解，直至收敛。主问题的对应形式为：

(23)

式中：i为迭代次数。

主问题实际上是原问题的一个松弛问题，计算后可得到主问题的目标函数，比原问题更优，因而是原问题目标函数下界。随着迭代进行，当上界与下界差足够小时，迭代停止。实际应用中，往往添加较少的约束就能很快收敛。

4 算例分析

以IEEE 14节点[24]、IEEE 118节点[6]系统为例，对半动态拓扑优化方法与静态和动态拓扑优化方法进行对比测试。编程基于GAMS Studio 27.3软件，调用CPLEX求解器进行MILP问题的求解，测试中所设置的CPLEX求解器的相对最优解收敛标准OptCR为0.1%，测试计算机配置为Intel(R) Core(TM) i5-6300U系列CPU，主频2.4 GHz，内存8 G。

4.1 IEEE 14节点系统

测试采用的IEEE 14节点系统中共有5台发电机，20条线路，对应的机组和线路参数分别见表1和表2。

表1 发电机组参数Table 1 Parameters of the generators

此外，文中电力系统运行方式辅助决策问题考虑的时间间隔为1 h。测试系统中各节点负荷及日前的负荷预测变化情况如表3与表4所示，同时，测试中目标函数采用插值线性化方法表示时选取的插值点数为6。

表3 节点负荷参数Table 3 Parameters of the bus load

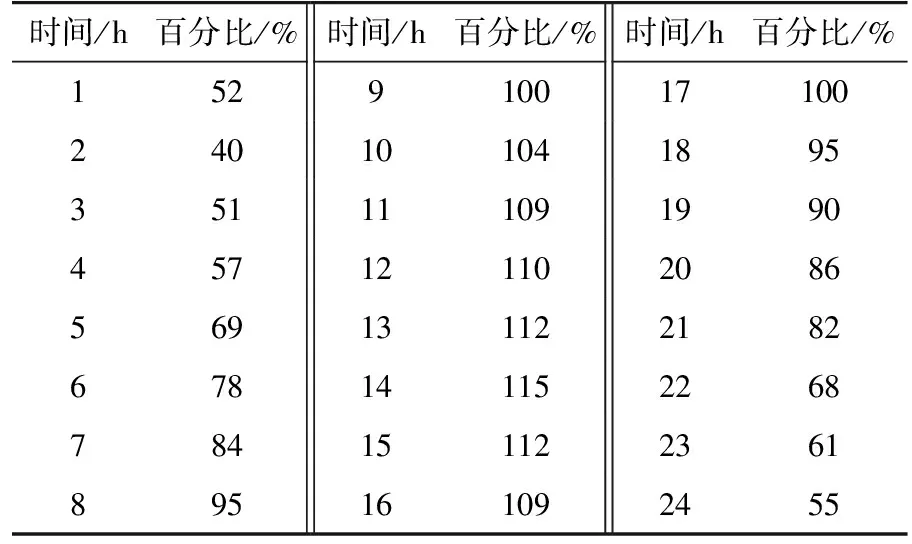
表4 节点负荷变化参数Table 4 Parameters of the bus load variation

4.2 静态网络结构优化对应结果

首先采用静态网络拓扑优化方法，对电力系统运行方式辅助决策模型进行求解，当网络结构允许改变的最大线路数C取不同数值时对应的目标函数及网络拓扑结果如表5所示。

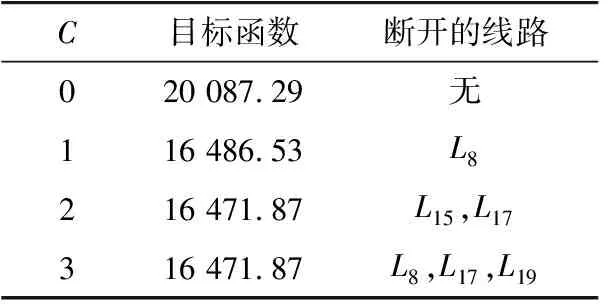
表5 静态网络结构优化对应的目标函数及拓扑结果Table 5 Objective function and network topology resultscorresponding to static network topology optimization

由表5可以看出，当断开的线路数小于等于2时，随着系统允许断开的线路数增加，系统的运行成本逐渐减小，之后再增加断开的线路数量系统的运行成本不再减少。这说明在此种网络结构优化方法下，网络的阻塞已经得到了最大程度的缓解，经济性好的机组功率输出能力已得到较为充分的利用，系统运行的经济性无法再通过此种手段得到进一步优化。

4.3 动态网络结构优化对应结果

采用动态网络结构优化方法，应用于电力系统运行方式辅助决策模型，当网络结构允许改变的最大线路数C取不同数值时，求解模型所得到的目标函数及网络拓扑结果如表6所示。

表6 动态网络结构优化对应的目标函数及拓扑结果Table 6 Objective function and network topology results corresponding to dynamic network topology optimization

由表6可以看出，与静态网络拓扑优化方法不同的是，随着系统允许断开的线路数增加，系统的运行成本逐渐减小，而且即便是允许断开线路数相同的情况下，动态网络结构优化方法可以灵活适应源-荷变化，从而可以充分发挥经济性较好机组的出力能力，所以经济性能提升更加显著。此外，因为系统在不同的负荷水平下网络中起关键阻塞作用的线路是不一样的，通过灵活地改变网络结构可以最大程度上减轻网络的阻塞程度，提升运行经济性。

4.4 半动态网络结构优化对应结果

将文中所提半动态网络拓扑优化方法应用于电力系统运行方式辅助决策模型，当允许改变的最大线路数C取值变化时，求解模型得到对应的目标函数值及网络拓扑结果如表7所示。

表7 动态网络结构优化对应的目标函数及拓扑结果Table 7 Objective function and network topology results corresponding to semi-dynamic network topology optimization

由表7可以看出，无线路断开时，半动态网络拓扑优化方法与静态和动态方法对应的目标函数均一致，说明了文中所构建模型的普适性。当允许断开的线路数为1时，半动态网络拓扑优化方法对应的目标函数与静态方法相同，高于动态方法，这表明此时半动态方法所能提升的经济性效果与静态方法相同，灵活性差于动态方法；当允许断开的线路数为2时，半动态网络拓扑优化方法对应的目标函数低于静态方法，高于动态方法，这表明此时半动态方法所能提升的经济性效果优于静态方法，灵活性虽差于动态方法但优于静态方法；当允许断开的线路数为3时，与静态方法不同，半动态方法对应的目标函数进一步减少，这表明此时半动态方法可以在一定程度上进一步减轻系统的阻塞程度，发挥经济性较好机组的出力能力，运行灵活性明显优于静态方法。

通过上述算例对比分析可知，文中所提半动态网络拓扑优化方法可以在不损失静态方法改善系统阻塞程度的前提下进一步减轻系统的阻塞，提升运行的经济性。

4.5 计算效率对比

采用IEEE 14节点与IEEE 118节点系统对上述3类网络拓扑优化方法对应的运行方式辅助决策模型计算效率进行测试，当允许断开的线路数C取值由小变大时，3类方法对应的模型计算时间如表8所示。

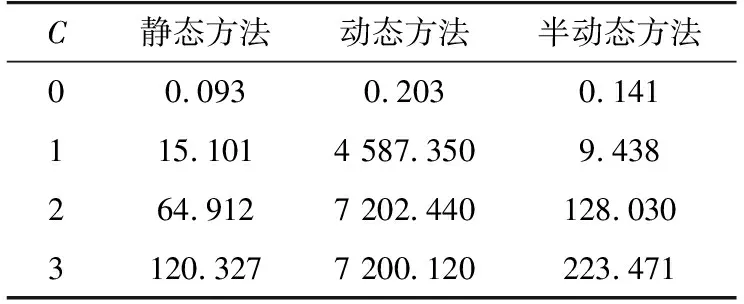
表8 IEEE 14节点系统3类方法计算时间Table 8 Computation time of three kinds of methods of IEEE 14 bus system s

需要说明的是，对于IEEE 14节点系统规模较小时采用直接求解MILP问题的方案，对于IEEE 118节点系统规模较大的情况下采用Benders分解法求解的方案，Benders算法所设置的收敛标准为上下界目标函数差小于等于0.1。此外，为了在一定时间内获得模型的有效解，采用文献[25]所提启发式方法，通过限定模型的最大求解计算时间为2 h(即7 200 s)，从而获得模型的次优解。

由表8可以看出，3类方法中静态方法具有较高的计算效率，且随允许断开线路数目的增加，计算时间变化并不显著。然而，对动态方法而言，由于线路组合情况随时间呈指数级增长，因此即便在开断线路数目为1的情况下，计算时间也接近1 h，而当开断线路数目为2或者更多时，模型求解在2 h内无法获得最优解，仅仅得到次优解，由此也说明了该类方法为提升网络运行灵活性而带来的计算效率低下的问题。对于文中所提半动态方法而言，随着允许开断线路数目的增加，模型的计算时间增长较快，但即便在线路开断数目为3的情况下，模型计算时间仍在4 min，说明文中所提半动态方法不仅可以兼顾系统运行灵活性，提升系统运行经济性，而且具有较高的模型解算效率。

由于IEEE 14节点系统在C为2时动态方法求解时间已达到上限(2 h)。因此对IEEE 118节点系统的模型解算效率进行测试时，采用Benders分解方法，测试结果见表9。

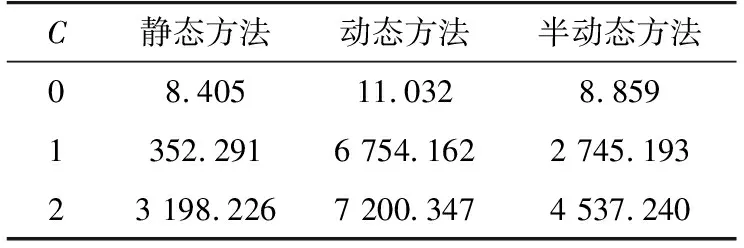
表9 IEEE 118节点系统3类方法计算时间Table 9 Computation time of three kinds of methods of IEEE 118 bus system s

通过表9可以看出，当采用Benders分解算法时，对IEEE 118节点系统，当C取0～2时，静态方法和半动态方法均可在限定的2 h内求解内完成求解获得最优解。然而，对于动态方法，在C取2的情况下只能在限定的2 h内获取次优解。由此说明了半动态方法计算上的显著优势，具有实际应用的可能性。

5 结论

文中首先对电力系统的静态与动态网络拓扑优化方法的优缺点进行阐述，进而提出了半动态网络拓扑优化方法，并构建了电网运行方式辅助决策的一般形式的数学模型，通过算例对比分析表明：

(1) 根据电力系统运行状态，基于网络拓扑优化方法辅助决策电网运行方式，可以减轻电网存在的阻塞，将有助于进一步提升电网运行的经济性和鲁棒性；

(2) 3类网络拓扑优化方法中，半动态网络拓扑优化方法的运行灵活性较静态网络拓扑优化方法优，提升系统运行经济性的潜力更大，但次于动态网络拓扑优化方法；

(3) 基于半动态网络拓扑优化方法所构建的电网运行方式辅助决策模型的解算效率较动态网络拓扑优化方法优势明显，且略低于静态网络拓扑优化方法，具有实际应用的可能性。