粗糙海面下的深海声传播特性*

冯丹平 李伟清

（中国人民解放军91388部队 湛江 524022）

1 引言

声波在深海的传播过程中会多次与海面产生反射，海面的反射系数会直接影响反射声波的强度。如果把海面简化为镜面，声波在其界面上的反射损失为零，这会使得声传播损失的计算结果偏大。实际上，由于受到风浪等的影响，海水表面是一种高低起伏的粗糙表面，这使得反射波的能量减小。王先华等［1］在简正波模型的计算中引入了海面的反射损失，计算了南海某海域的传播损失，并通过实测数据的对比，证实了在该海域海面波浪起伏对声传播的影响很大，在仿真计算中需考虑其影响。陈文剑等［2］研究了随机起伏海面的散射对水声信道特性的影响规律，其研究结果表明传播损失与海面风速以及声波频率呈正相关。姚美娟等［3］对比了几种典型的粗糙海面下声传播损失的计算方法，并结合实测数据，说明了在声传播损失中考虑海面反射损失的必要性。

本文首先研究了粗糙海表面的声反射系数受海况和声波频率的影响规律，并使用射线模型仿真了不同海况下的声传播损失。仿真结果表明，频率一定的情况下，声反射系数随着海浪有效波高的增加而减小，声传播损失随着海浪有效波高的增加而增加。在近距离时，海浪对声传播损失的影响很小，当传播距离达到50km左右时，3级海况时的声传播损失较平静海面时的大约高5dB，当传播距离达到100km左右时，这个差距扩大到了大约10dB。

通过海上实验的实测数据与仿真结果对比发现，在考虑粗糙海面声反射损耗的情况下，仿真结果和实测数据能很好地吻合。如果简单地将海面简化为镜面，仿真则明显小于实测数据。这说明粗糙海面的声反射系数分析是声传播损失仿真计算中不可或缺的一个环节。

2 粗糙海面的声反射理论

在计算粗糙表面散射的问题上，经典的近似方法主要有Kirchhoff近似法［4～5］和基于瑞利假设的微扰法［6～7］，Watson［8～9］在瑞利假设的基础上给出了声反射、声散射和吸声收的表达式，Voronovich［10］在微扰近似的基础上提出了小斜率近似法。小斜率近似法在掠射角不是特别小且表面斜率不是特别大的条件下计算粗糙表面的声散射是非常有效，能够很好地满足海洋声场计算中对海水表面反射系数的计算需求。

首先将粗糙的海水表面简化为由多个不同振幅、频率、初始相位的正弦波或余弦波叠加而成，假定粗糙的海表面高度满足高斯分布，其功率谱密度函数满足

式中，K为空间波数，l为相关长度，σ为波浪的均方根高度。

可以模拟出粗糙海面的高度样本为

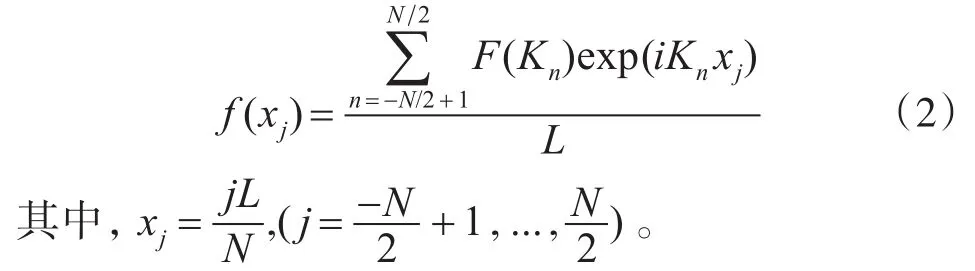
表示第j个采样点，L为样本长度：

当波数为k的声波以θ掠射角射入时，通过求解散射强度，并且对整个表面进行统计平均，可以得到近似的平均海面反射系数。

图1为三种掠射角情况下，反射系数随波浪均方根高度的变化曲线，从图1可以看出，当均方根高度小于0.2m时，平均反射系数接近于1，此时海面相对平静，可以近似为镜面，但是当均方根高度大于0.2m后，海面的平均反射系数逐渐减小，此时海面的反射损失就不能被忽略。下面将通过仿真计算，研究0级海况、2级海况和3级海况这三种情况下的传播损失，并结合实测数据验证仿真计算结果。

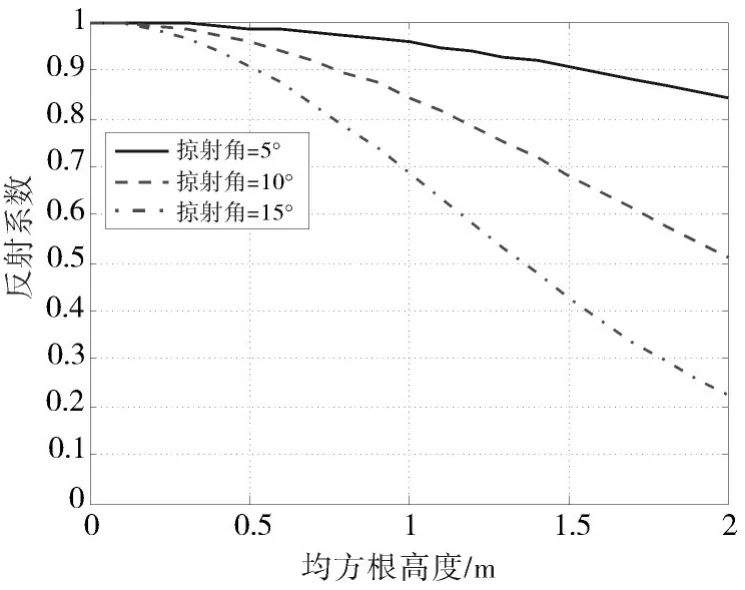
图1 反射系数（f=400Hz）

3 仿真研究

Wenz［11］描绘了不同海况下的海面状况参数，本文根据Wenz的结论，分别认为0级海况的海浪均方根高度σlevel0=0m，2级海况的海浪均方根高度σlevel2=0.5m，3级海况的海浪均方根高度σlevel3=1m，并将分别计算这三种情况下的深海声传播损失。本文使用的声场计算模型为BELL⁃HOP，它是基于高斯声束追踪法［12］开发的，具有无需计算本征声线、计算速度快、稳定性好等优点，并且该模型的计算精度与全波动理论计算结果相近，非常适合计算深海高频声传播。

在某海区，分别将这三种海况下海面反射系数的计算结果作为模型的输入文件，对该海域的传播损失进行仿真计算。仿真中，声源的频率为400Hz，声源深度为300m。图2为接收深度200m处三种海况的声传播损失对比。

图2 深度200m处的声传播损失对比

从图2可以看出，随着海况的恶化，声影区的传播损失逐渐增大，但是汇聚区的传播损失变化不大。在二级海况和三级海况情况下声影区的能量明显小于平静海面时声影区的能量，并且在三级海况时声影区的传播损失大于二级海况时的。就汇聚区而言，海面对汇聚区附近传播损失的影响较小。由于汇聚区的主要由海水中弯折的声线汇聚而成，这部分声线不与海面发生接触，因此海面的衰减对其影响不大。

4 实测数据分析

为进一步说明海况对声传播损失的影响，本文将深海海域中两条测线上的声传播实测数据与仿真计算的结果进行对比。在仿真中，分别计算考虑和不考虑海面反射损失这两种情况时的声传播损失。图3的圆形为声传播测线一的实测数据，实验中爆炸声源深度为300m，接收深度为197m，分析的频率为200Hz，实验时的海况为二级海况。虚线和实线分别为同条件下平静海面以及二级海况时的声传播损失。图4中分析的频率为400Hz，其他条件与图3中的一致。

图3 测线一实测和仿真对比（200Hz）

图4 测线一实测和仿真对比（400Hz）

图5的圆形为测线二的实测数据，实验中爆炸声源深度为100m，接收深度为200m，分析的频率为200Hz，实验时的海况为二级海况。虚线和实线分别为同条件下平静海面以及二级海况时的声传播损失。图6中分析的频率为400Hz，其他条件与图5中的一致。

图5 测线二实测和仿真对比（200Hz）

图6 测线二实测和仿真对比（400Hz）

从图3～图6可以看出，实测数据基本上与二级海况时的仿真计算结果相吻合。

从汇聚区的声传播损失来看，无论是实测数据还是两种平静海面和二级海况时的仿真结果，均在80dB～90dB之间，并且它们之间的差异较小。由于在实验海域深海声道的作用下，汇聚区的声线均几乎不与海面接触，因此汇聚区内的声传播损失几乎不受海面的影响。这说明在不考虑海面传播损失时，仿真模型的计算结果相对准确，能够很好地接近实测数据。

但是从声影区的仿真和实测结果对比可以看出，实测的声传播损失明显大于不考虑海面反射损失时的仿真结果，其差异高达30dB。这是由于仿真中未计及海面反射损失，从而导致声传播损失计算结果偏小。当在仿真计算中考虑海面反射损失后，其结果便接近于实测数据。这证明了仿真计算中考虑海面反射损失的必要性。

5 结语

本文在声传播损失的仿真计算中，考虑了粗糙海面引起的反射损失，研究和探讨了海况对声传播损失的影响特点。仿真结果表明随着海况的恶化，海面的声反射系数逐渐降低，从而导致声传播损失不断增大。本文将声传播实验的实测数据与仿真计算结果作对比，发现只有在计及海面反射损失后，仿真结果才能以很好地与实测结果相吻合，这进一步印证了海面反射损失是仿真计算中不可忽略的因素。