基于合作目标的单目视觉位姿估计*

范路生 张静远 王为如 吴佩璋

（1.海军工程大学 武汉 430000）（2.中国船舶集团有限公司第七一三研究所 郑州 450015）

1 引言

在传统物流行业中，叉车是一种工业的搬运车辆，常常被用来装卸、堆垛物品［2］。在新兴的无人物流行业中，叉车自主叉取货物可以节省大量的人力物力成本，提高效率［1］，货叉与货叉孔的高精度相对位姿估计是叉车自主叉取货物的关键问题。基于视觉的位姿估计具有精度高、成本低、非接触、实时性高、位姿信息量丰富等突出优点［3］。故本文提出了一种基于单目视觉的目标相对六维位姿估计方法，用来计算货叉与货叉孔的相对六维位姿。

在现有的大多数基于视觉的位姿估计方法中，有两个基本步骤：特征提取和位姿参数求解［4］。提取的特征分为合作目标特征和非合作目标特征两大类，基于合作目标特征的位姿估计方法需要在被测目标物上设置一些几何结构信息已知且能够在相机中完整清晰成像的合作标志。人为设置的标志点能大幅度提高目标的检测精度和位姿估计精度［5～6］，具有结构简单、特征明显、易于分辨以及测量精度高等优点。常见的合作标志包括十字、圆形、对角、Aruco码等［7］，相比于其他合作标志，Aru⁃co码角点可以提供丰富的位姿估计对应信息，同时其内部特有的二进制编码使得标志在错误检查和修正方面保持一定的稳定性。因此本文选择Aruco码作为合作标志，布设在货叉孔附近，相机布设在货叉附近。

提取的合作目标特征用于构建2D-3D对应关系，根据构建的对应关系实现位姿估计［4］。根据被测目标的特征信息，分为基于点特征的位姿估计方法，基于直线特征的位姿估计方法，基于圆的位姿估计方法等。由于Aruco码特征点信息丰富，本文解算方法利用的特征主要是特征点。

在已知相机内参的情况下，由特征点与其像点的对应关系求解目标空间坐标系相对于像机坐标系的相对位姿关系就是经典的PnP问题（Perspec⁃tive-N-Point），即N点透视问题［8］。PnP问题求解方法大致分为线性算法和非线性迭代算法两类。P3P最多有4个解，Gao等通过吴方法［9］给出其完全解分类。Quan和Lan［10］对于P4P和P5P问题给出了线性SVD算法，他们把PnP问题转化成多个P3P问题，算法计算复杂度为O(n5)。Fiore［11］提出了一种计算复杂度为O(n2)的线性算法，但对噪声比较敏感。Moreno和Lepetit提出了一种计算复杂度为O(n)的高效、高精度线性算法EPnP［12］，但经过实验验证，EPnP算法对图片的深度信息比较敏感，当深度较小时，该算法精度不高。另外一个典型的线性算法是直接线性变换（Direct Linear Transformation，DLT）算法［13］，它将变换矩阵12个变量当成独立变量，忽略旋转矩阵的正交约束，得到12个线性约束方程，当特征点个数N≥6时，该算法有唯一解。DLT算法计算速度快，但受噪声影响较大，精度不高。经典的非线性迭代算法是以最小化某种代价函数为目标，将位姿求解问题转换为非线性最小二乘问题，利用Gauss-Newton法或者Levenberg-Mar⁃quardt法等非线性优化算法进行迭代求解。非线性迭代算法精度高，具有很高的抗噪声性能，但该方法计算量远远大于线性算法，求解过程非常耗时，对迭代的初值非常依赖。

本文提出了一种基于合作目标特征点定位技术的位姿估计算法，可有效快速解算货叉与货叉孔的相对六维位姿，该算法先利用N（N≥6）个特征点通过DLT算法求解得到货叉与货叉孔相对位姿的初值，再将该值作为非线性迭代运算的初值，使用重投影误差来构造代价函数，经过数次迭代，则可得到两者高精度的六维位姿。

2 原理

2.1 视觉位姿估计模型

按照本实验构建相机透视投影成像位姿估计模型［14］，设相机坐标系OC−XCYCZC，基准坐标系（货叉坐标系）O−XYZ，世界坐标系（货叉孔坐标系）OW−XWYWZW，图像坐标系o−uv，坐标系示意图如图1所示。

图1 坐标系示意图

本文视觉位姿估计模型：

其中K表示像机内参矩阵，[RC|TC]、[R|T]分别表示相机坐标系相对于基准坐标系的旋转平移矩阵、基准坐标系相对于世界坐标系的旋转平移矩阵，s是比例系数，其值是一个常数。

由于像机镜头是由凹、凸透镜及其组合构成的，因此，成像平面不同区域对光线的弯曲程度也是不同的，从而造成图像中实际点像素坐标(x，y)与理想点像素坐标(xcorr，ycorr)之间的像差，该像差会导致图像出现径向畸变和切向畸变，对像点产生的影响［15］可以描述为

式中，r2=x2+y2，是像素点p到图像中心的距离，k1、k2、k3是径向畸变参数，p1、p2是切向畸变参数。本文采用Matlab标定工具箱对相机标定，得到相机内参fx、fy、cx、cy和畸变参数。将线性模型式（1）与像差模型式（2）组合起来构成完整的针孔像机透视投影模型。

2.2 直接线性变换

根据针孔相机2D点到3D点齐次坐标矢量的映射关系，本文定义投影矩阵M：

令u=[uv1]T，XW=[XWYWZW1]T，则式（1）可以简化为：

将投影矩阵M的第j行记作mjT，将矢量式su与MXW进行叉乘运算，可得到：

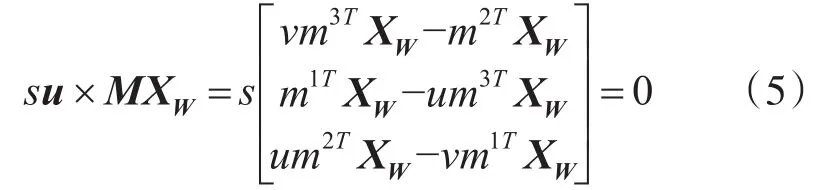
通过矩阵线性变换，化简可得到关于M的三个方程：

忽略3×3旋转矩阵R的正交约束，将其看作9个独立变量，则M的每个元素都为独立变量，依据矩阵秩的特性，通过推导得到两个独立方程，共有12个独立未知变量，即基准坐标系相对于世界坐标系的旋转平移矩阵参数。

依据式（7），每个合作目标特征点可提供两个独立方程，当特征点的个数N≥6时，理论中则可得到唯一解。

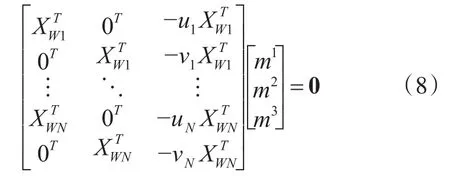
当N>6时，采用最小二乘的方式拟合得到12个独立未知变量的值，求解得到基准坐标系相对于世界坐标系的旋转平移矩阵，即货叉与货叉孔的相对位姿的初值。通过实验验证，仅采用DLT求解得到的位姿精度较低，我们可以通过最小化重投影误差来提高精度。

2.3 光束法平差模型优化

BA（Bundle Adjustment），译为光束法平差，其本质是一个优化模型，目的式最小化重投影误差。重投影误差是真实三维空间点在图像平面上的投影ui（即图像上的像素点）和重投影vi（用3D点按照当前计算到的投影矩阵进行第二次投影计算得到的虚拟的像素点）的差值。

图2 重投影误差

单个点的重投影误差为

BA模型是将所有重投影误差的和最小化：

针对BA模型的优化算法有很多，本文采用非线性算法Gauss-Newton对上节求得的目标间的相对位姿初值进行优化。结合位姿估计模型及求解式（7），本文利用特征点重投影误差构造代价函数Fui，Fvi，通过多次非线性迭代优化使其最小化，可使所有特征点的重投影误差和的最小化。

依据旋转平移矩阵[R|T]组成元素特性，设代价函数变量为各轴旋转角度和平移距离，即pe=[Ax，Ay，Az，Tx，Ty，Tz]T，分别对代价函数Fui，Fvi求一阶偏导数，则可得到雅可比矩阵：

Gauss-Newton算法是忽略代价函数的泰勒展开式二次项及多次项：

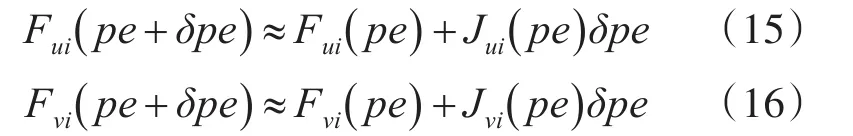
考虑到重投影误差ei=‖ui−vi‖ 的理想值为0，故我们直接令代价函数为0，则可以演化得到本文BA优化模型：

通过最小二乘拟合，经过数次运算，可在δpe方向上迭代直到代价函数绝对值最小，得到货叉与货叉孔的高精度六维位姿。

3 实验

基于上章节算法原理，相机坐标系相对于基准坐标系的旋转平移矩阵[RC|TC]可通过调整基准坐标系与世界坐标系完全重合，即将货叉前端与货叉孔前端完全重合，则可得到。视觉位姿估计实验设计如图3所示。

图3 视觉位姿估计实验流程图

本文实验采用USB插孔的工业级红外摄像机，在实验过程中，货叉前端距离货叉孔前端景深距离为0.5m，相机距离合作目标1.58m。相机采集图像过程中，货叉、货叉孔、相机相对于地面保持静止，经过位姿解算，得到500组实验数据，实验结果如下所示。

在本次实验中，本文得到了500组货叉与货叉孔相对六维位姿参数实验数据，如图4所示，经过各参数实际值与估计的对比分析，我们可以得到，X轴平移距离Tx静态误差在2mm左右，动态误差在［-0.1mm，4.1mm］区间，X轴旋转角度Ax静态误差在0.05°左右，动态误差在［-0.04°，0.12°］区间；Y轴平移距离Ty静态误差在-1.5mm左右，动态误差在［0.9mm，-3.9mm］区间，Y轴旋转角度Ay静态误差在0.06°左右，动态误差在［0.1°，0.11°］区间；Z轴平移距离Tz静态误差在0mm左右，动态误差在［-1.5mm，2mm］区间，Z轴旋转角度Az静态误差在-0.06°左右，动态误差在［-0.15°，0.05°］区间。

图4 视觉位姿估计实验结果图

经过实验验证，在相机距离合作目标景深距离1.58m，货叉距离货叉孔0.5m时，本文位姿估计算法平移距离精度达到毫米级，旋转角度精度在0.2°以内。

4 结语

本文以至少六个共面合作目标特征点定位技术求解货叉与货叉孔的相对位姿，基于针孔相机透视投影模型构建视觉位姿估计模型，采用直接线性变换解算得到两者相对位姿测量的初值，依据最小化重投影误差的原则构建代价函数，并用Gauss-Newton非线性迭代算法对其进行优化，提高位姿估计精度。实验结果表明，在理想状态下，平移距离误差最大为4.8mm，旋转角度误差最大为0.2°。但同时我们也可以得到该算法估计值波动范围较大，后期应分析原因，增加滤波算法进一步改进优化。