基于改进遗传算法的汽车混流装配线排序优化

刘冠权 奚 浩 王 越 王志远

(青岛理工大学管理工程学院 山东 青岛 266520)

0 引 言

互联网、物联网时代到来，顾客消费需求升级，不再满足于单一模板化，向个性定制化过渡发展，混流装配线作为一种可以实现多品种产品的装配线可以更好满足顾客需求的多样化。因此高鲁棒性、高柔性混流装配线的排序问题将成为制造业生产运作优化的重要问题。

Drexl等[1]对汽车投产排序问题提出了整数规划(Integer Programming，IP)模型并进行求解；Fliedner等[2]在此基础上进一步修改了目标函数并采用分支定界法求解此类问题。郑敏等[3]建立了涂装切换成本和总装车间人工成本最小化的两个目标函数模型，并用CPLEX数学规划软件对其进行优化求解。

当混流装配线排序问题规模比较小时，上述数学规划方法虽然能够得到较好的解,但对于大规模问题，短时间内很难找到最优解。因此，近年来大多数专家用启发式算法以及现代智能优化算法来解决这类问题。

郑永前等[4]针对混装线排序问题，从装配线总闲置-超载成本最小化角度，建立了数学模型并设计粒子群算法进行求解；黄健等[5]则在前者基础之上，加入产品变化率、总切换时间的目标，在离散系统仿真软件Plant Simulation平台进行仿真，并结合总工时最小化目标，采用遗传算法得出一组满意解，最后从混装线平衡角度对得到的满意解进行分析,得到满足目标的最优解。刘琼等[6]同样建立了以最小化工作站闲置/超载总成本、产品变化率和产品切换总时间为目标的多目标优化模型，但设计了一种改进多目标猫群优化算法对该问题进行应用。李修琳等[7]从串并行线与总装线投产序列差异度最小和总装物料消耗平顺化角度，建立了多目标关联排序模型。江新利等[8]研究了某冷柜公司生产系统中具有有限缓冲的两生产阶段排序问题,并设计了一种库存量计算算法来更好地计算空模数量与在制品库存数量，通过改进遗传算法求解了两个生产阶段的排序问题。甘雅文等[9]建立了以工作站堵塞时间最小化与产品切换次数最小化为目标的混装线排序模型，首次引入主客观优化评价算法对模型进行求解。Chutima等[10]则考虑了三个相互冲突的目标，包括最小化油漆颜色变化的数量、最小化比率约束违规的总数、最小化效用工作，并提出了扩展重合算法(COIN-E)求解该问题。

综上所述，启发式算法和现代智能优化算法与数学规划法相比较而言，能够更好地解决该问题。基于此，以汽车混流装配线为研究对象，从最优化投产车型序列进入各工位总等待装配时间(一个最小生产循环周期)的角度，建立数学模型，并设计出一种改进的遗传算法进行求解，得到了最优车型排序。与标准遗传算法进行对比分析，体现了本文算法的优越性。该算法改进之处在于其“定长”实数编码、“定序模式”改进的自适应单点交叉、交换变异算子的设计避免了不可行解的产生，同时在选择操作还引入精英保留策略，保证最优后代不被丢失，极大提高了算法的性能。最后通过Flexsim软件分别对最优车型排序和实际生产中的车型排序进行了仿真与对比。

1 数学模型

1.1 问题描述

混流装配线排序问题是根据产品订单信息将不同类型产品排成一个投产序列，并以此投产序列来组织混流装配线的生产[11]。

在汽车混流装配线中，投产车型排序采用最小生产循环模式(Minimum Part Set，MPS)，即整个装配顺序由重复的MPS构成。MPS由各车型的订单需求数量比例构成最小投产序列，只需将MPS进行排序，并让其结果循环N次，即可得到整个投产顺序。

1.2 相关符号的定义

n表示混流装配线的工位总数；d代表一个MPS循环中投产车辆数量；N表示每天循环总次数，即每天各车型订单需求量的最大公约数；D表示某汽车企业mes系统中每天接到各车型订单数量总数；i表示第i个投产车辆，i取1,2,…,d；j表示第j个工位，j取1,2,…,n；k表示第k种车型，k取1,2,…,K,其中K表示装配线可生产的车型种类为K种;qk表示一次循环中各种车型的投产数量；Tij表示第i个投产车辆在第j个工位的等待时间；Bij表示第i个投产车辆在第j个工位开始装配的时刻；Fij表示第i个投产车辆在第j个工位结束装配的时刻；xik表示为第i个投产车辆是k型的，取值为 0 或 1；tkj表示k型车辆在第j个工位的作业时间；v表示车辆的投放速率(固定值)。

1.3 目标函数及约束条件

建立的目标函数及约束条件如下：

(1)

(2)

(3)

(4)

Bij=max(Fi(j-1),F(i-1)j)B11=0

(5)

Tij=max(0,F(i-1)j-Fi(j-1))i=2,3,…,d，j=2,3,…,n

(6)

(7)

(8)

目标函数式(1)的含义为一个最小生产循环周期内各车型经过n个工位等待装配时间最短；式(2)可保证每个工位只能同时装配一个车型；式(3)表示一个最小生产循环周期投产车辆数量是由订单总量与各车型需求量的最大公约数确定的，且等于一个周期内每个车型投产数量总和；式(4)表示第j工位上的第i个投产车辆的装配完成时刻与开始装配时刻的关系约束；式(5)表示第j工位上的第i个投产车辆装配开始时刻是取第i个投产车辆在第j-1工位上完成时刻与第i-1个投产车辆在第j工位完成时刻的最大值，第1个车辆在第1个工位开始时刻为0时刻，后面车辆的投放以此为基准时刻；式(6)表示第i个投产车辆在第j个工位上的等待时间，即如果前一个投产车辆在该工位的完成时刻大于该投产车辆在前工位的差值，则等待时间为两者之差，反之，即在该投产车辆前工位完成装配之后立即去到下工位进行装配，等待时间为0；式(7)表示当为第1个投产车辆进入装配线的每个工位都不需要等待，则值为0；式(8)表示从第二个投产车辆开始，在一个最小循环投产周期内，各车型进入第1个工位进行装配的总等待时间。

2 改进遗传算法设计

在标准遗传算法(Simple Genetic Algorithm，SGA)基础上提出了一种改进遗传算法(Improved Genetic Algorithm，IGA)。从编码上，根据车型字符串特征及MPS约束，设计了特有的“定长”实数编码，并且提出一种基于“定序模式”的改进自适应单点交叉算子以及交换变异算子，避免了不可行解的产生，同时选择策略改进方面在标准遗传算法轮盘赌选择的基础上引入精英保留策略，保证经过遗传操作优秀个体不被破坏。

2.1 编 码

编码依据混流车型种类为字符串的特点，设计了字符与实数编码转换的“定长”实数编码方式。如图1所示，MPS为20，四种车型A、B、C、D数量分别为7、6、3、4。即车型A为1-7的定长实数范围，车型B为8-13的定长实数范围，车型C为14-16的定长实数范围，车型D为17-20的定长实数范围。通过随机数产生一排序列与字车型相对应。

图1 “定长”实数编码示意图

2.2 初始化种群

初始种群的产生好坏不仅会直接决定进化的优劣，而且优良的初始种群将提高算法的运行效率。初始种群产生的步骤如下：

Step1生成一个实数编码车型排序序列，设置合理的初始种群数量、最小循环周期车型数量(序列长度)参数。

Step2将车型排序序列中每个编码的车型用随机数进行随机排序生成新的序列，序列个数(即初始化种群个数)由初始种群数量决定。

2.3 适应度函数设计

适应度函数的数值大小体现了个体优劣的程度。本文适应度函数设计为f(x)=T-g(x)，其中g(x)为目标函数，T为固定值，这里取值为一天有效工作时间。目标函数越小，则适应度函数值越大，那么说明个体越优良。

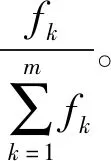
2.4 选择算子和精英保留

在标准遗传算法轮盘赌选择算子的基础上，引入精英保留策略。因为如果以产生的子代作为父代进行交叉、变异等操作产生新个体时，会丢失很多优良的基因，所以采用精英保留(Elitism)策略能够更好地保存较优个体而不被丢失，其原理是将当前最优解复制到新个体中，即算法的任何时刻最优解都能被保留。

2.5 交 叉

交叉算子在传统单点交叉基础上，提出了一种“定序模式”的改进自适应单点交叉，其步骤如下：先用随机数确定交叉的位置，即根据此位置点可以把父代1分为两个部分Part1和Part2，在进行交叉时找到要交叉的父代2个体里与Part1相同的部分，以及与其不相同的车型以外的部分，保持序列顺序不变依次替换Part2，形成新一代子代1，而相同的车型部分保持序列顺序不变，用父代1的Part1部分依次替换，如图2所示。

图2 “定序模式”的单点交叉示意图

2.6 变 异

变异操作采用交换变异。同样都采用随机函数的方法确定两个变异点point1和point2，最后将对应位置的两个车型进行相互交换，具体操作如图3所示。

图3 交换变异操作示意图

综上所述，本文设计的改进遗传算法思路如图4所示。

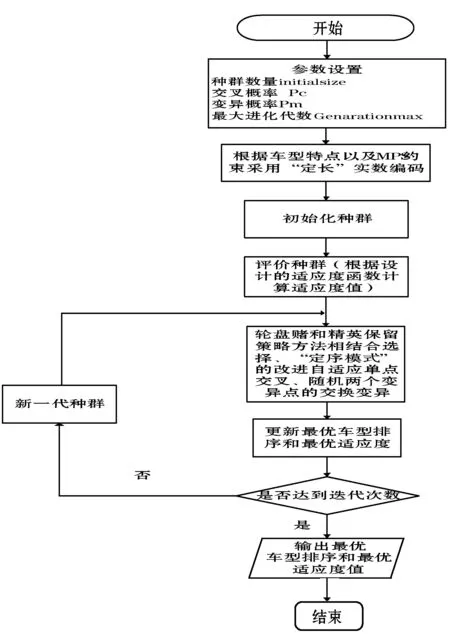
图4 改进遗传算法的流程图

3 实例分析

3.1 混流装配线现状

总装车间是整车厂的重要组成部分，其工艺最为复杂。它是将汽车零件在经过冲压、焊接、涂装三大工序后的空车身进行装配。以国内某车企的现总装车间装配线上的L-CAR、SRV、SGM12及SGM18这四种车型作为分析对象，分别用A、B、C、D字母依次进行编号，该混流装配线上现用投产车型排序以AAAA AAACCCDDDDBBBBBB进入装配线。主要工艺流程及工序内容对应的编号如图5所示。

图5 总装车间装配主要工艺流程与工序内容

3.2 基础数据

由企业MES系统获取订单信息，可得4种类型产品每天产量分别是126、108、54、72台，共计360台。可得一个MPS循环内4种产品比例为7 ∶6 ∶3 ∶4。分早、中2班生产，每班的实际生产时间为7.6小时。根据上述工艺流程及实际企业工厂布局，把30道工序划分为8个工位,相关数据如表1所示。

表1 装配线各工位及四种车型不同工位的装配时间

3.3 MATLAB对模型求解

将SGA和IGA分别在通用计算软件MATLAB R2012a上运算，初始化参数设置如下：种群数量为100，交叉概率Pc=0.9，变异概率Pm=0.05，进化的最大代数为100，得到的适应度进化曲线如图6所示。前者得到最优排序为1、7、8、9、13、3、4、19、15、10、16、2、6、20、17、11、14、5、18、12，解码得AABBBAADCBCAADDBCADB，适应度函数值为54 036，目标函数最小值684；而后者得到的最优排序为3、1、4、6、13、10、9、17、12、18、20、2、8、16、15、5、7、14、19、11，解码得为AAAABBBDBDDABCCAACDB，此时，适应度函数值为54 311，目标函数最小值为409。基于上述数据对比分析可得，本文提出的IGA在该问题的优化上比SGA更有效。

图6 适应度进化曲线

4 汽车混流装配线的Flexsim仿真

4.1 Flexsim仿真软件

Flexsim仿真软件是美国 Flexsim公司开发的一款三维的通用物流仿真软件，采用C++语言开发，支持离散系统和连续流体系统的建模。文献[12]运用Flexsim仿真软件，可以较容易建立上述各工位仿真三维模型，并通过设置各实体(即工位)具体参数，运行模型得出有效的仿真数据，最终优化设计或改造方案。因此，采用Flexsim软件建立该装配线仿真模型，这里使用的版本为Flexsim 2018。

4.2 仿真元素定义

仿真模型里的实体代表着实际生产中的生产元素，具体定义如表2所示。

表2 仿真元素定义

4.3 基于Flexsim的汽车混流装配线仿真模型

1) 建立混流装配线的Flexsim仿真模型。

根据所划分的8个工位，同时为了更好模拟投产车型等待装配的状态，在两个工位之前都加入一个暂存区，依次生成所有实体并修改每个实体的名称以匹配8个工位内容，并进行“A”连接，模型如图7所示。

图7 汽车混流装配线的Flexsim仿真

2) 各实体的参数设置。

(1) 对发生器进行参数设置。该仿真模型以固定投产方式投产，故在发生器的到达方式选项卡下选择“到达时间表”，并在ArrivalTime列每隔145 s设置一个到达时刻。同时按照MATLAB求解的投产序列进行设置，具体ItemType列的1、2、3、4分别对应A、B、C、D种车型，即某车企L-CAR、SRV、SGM12及SGM18这四种车型。MPS为20，Arrivals设置为21，最后1行参数设置主要是保证其按照一个MPS进行循环，其数量Quantity设置为0，ItemType设置为一个MPS中的第一个车辆类型，即设置为1。同时在发生器离开触发里添加代码，将4种类型的颜色分别设置为蓝色、黄色、绿色、黑色。根据每天订单数为360台，设置关闭和打开端口，其条件为getoutput(current)==359，发生器到达时间表部分参数设置如图8所示。

图8 发生器到达时间表部分参数设置

(2) 设置处理器的参数。对8个工位处理器实体的加工时间分别进行设置，具体参数的设置，根据表1的四种不同车型装配时间不同，设置4个case，每个case分别对应一个车型装配时间。

(3) 设置传送带的参数。根据实际生产中全天订单完成数量进行设置，即当传送带送走359台车辆，模型自动停止仿真，代码设置为if(getoutput(current)==359)stop；

(4) 设置统计数据，使用Flexsim中Dashboards的停留时间模块，并选择按类型统计停留时间进行仿真分析，分别选中每个暂存区，将类型标签设置为ItemType，值数据类型设为number。

4.4 模型的运行

按照上述步骤建立的仿真模型，点击“运行”按钮运行该模型，仿真模型运行完成之后，点击设置的统计数据中Dashboards的按类型统计停留时间模块，从高级选项卡的查看表中记录数据，并计算得出完成全天订单总等待时间。同理按照上述操作再对SGA得出的投产排序及该企业实际生产线上现有汽车车型投产排序进行仿真。三种不同的车型投产顺序仿真实验结果如表3所示。

表3 仿真实验结果

5 结 语

针对汽车混流总装线投产排序问题，建立了以一个循环周期内的车型经过各工位等待装配的总时间最短为目标的数学模型。通过对某企业混流总装线的工艺流程、车间布局等进行分析，把划分的工位以及每个工位的标准工时作为数据基础。基于MATLAB平台开发了算法程序求解该模型，并将标准遗传算法与本文改进的遗传算法进行了对比分析，发现所提出的IGA更有效。最后运用Flexsim软件分别对原投产排序、SGA与IGA得出的排序进行了仿真，发现IGA得出的最优排序完成全天订单总等时间最短，验证了该算法的有效性。

本文研究对制造企业实施JIT，做好均衡化生产，确保产品投产排序的有效性和可行性，顺利推进混流生产以满足顾客多样化需求具有指导性意义。