背板对氧化铝陶瓷薄板断裂锥形态的影响
余毅磊,蒋招绣,王晓东,任文科,杜忠华,高光发,2
(1.南京理工大学 机械工程学院,江苏,南京 210094; 2.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
提 要:采用弹道侵彻试验与有限元数值模拟相结合的方法,研究了背板条件对氧化铝薄板陶瓷/金属复合装甲在抗12.7 mm穿燃弹过程中形成的陶瓷锥角大小与形态的影响,并分析了陶瓷锥形成的过程与机理.结果表明:背板厚度对于陶瓷锥大小的影响尤为明显,当背板厚度增大时,主裂纹汇聚的交点越靠近弹靶接触面,此时拉剪裂纹的扩展起到了主要作用,当背板厚度与陶瓷厚度之比小于1时,厚度比每增大1/6,陶瓷锥锥角大小增加5%;当界面间波阻抗差值减小即背板材料波阻抗升高时,从界面反射的应力波减弱,从而减小了对陶瓷的损伤,陶瓷断裂锥锥角大小也随之减小.
近年来,防护结构呈现出高性能和轻量化的需求,而陶瓷/金属复合靶板兼有陶瓷高硬度和金属高韧性的优点,抗弹性能优异,在航空、轻型装甲车辆的防护领域得到了广泛应用.在薄复合靶板中,陶瓷与金属背板如何组合才能发挥出各自的优势,是对于陶瓷轻型复合装甲研究中需要解决的基础性问题.自20世纪60年代Wilkins等进行试验研究以来,国内外学者对于厚陶瓷靶板的抗弹性能及机理进行了大量的研究,但是对于薄陶瓷结构复合装甲的抗弹性能的研究较少.DOP实验表明[1-4],在陶瓷板中,不同层之间界面对弹体的阻碍作用随背板材料波阻抗的增加而降低.在侵彻过程中陶瓷板内形成的陶瓷锥吸收弹体的冲击动能、传递冲击载荷,改变背板的破坏形式,增大背板的破坏程度,是提高靶板的抗弹性能的主要机理.其中陶瓷锥的大小和形态是影响陶瓷抗弹性能的主要因素之一,现有研究表明[5-7],薄板陶瓷的陶瓷锥锥角接近65°,但均基于对特定材料及组合方式的陶瓷复合装甲进行的测量,尚未对薄板陶瓷复合装甲中陶瓷锥的大小与背板条件的关系做出研究.
文中采用弹道冲击试验与仿真模拟相结合的方法研究了12.7 mm穿甲燃烧弹冲击下陶瓷/金属复合薄靶板的冲击响应,对薄陶瓷靶板中陶瓷断裂锥的大小形态及裂纹形成进行了描述,重点分析了背板厚度及背板材料对陶瓷断裂锥形态及大小的影响规律.
1 侵彻试验及其结果
1.1 试验设计
具体实验装置布置如图1所示,从左至右依次为12.7 mm口径火药推进弹道枪,光幕测速系统和陶瓷复合靶板.其中光幕测速系统测速精度为±2 m/s.采用12.7 mm标准穿燃弹对陶瓷/金属复合靶板进行撞击,弹丸主要由铜被甲、燃烧剂及弹芯组成.其中,穿燃弹弹芯质量约为29.8 g.

图1 试验现场设置Fig.1 The design of test site
图2为陶瓷/金属复合靶板结构及靶板固定装置示意图.实验中通过约束框对整个靶板进行固定,具体陶瓷/金属复合靶板结构由金属面板、Al2O3陶瓷板、金属背板构成.其中,面板材料为2 mm厚度的2024铝合金,背板材料包括不同厚度的Q235钢或2024铝合金,陶瓷板则由九块氧化铝陶瓷块(100 mm×100 mm×12 mm)拼接构成.此外,实验中用不同厚度(2 mm、4 mm、6 mm、8 mm)Q235钢作为背板材料的陶瓷/金属复合靶板,用于研究金属背板厚度对陶瓷锥形态的影响,且以此通过对比4 mm厚度2024铝合金背板材料所组成的陶瓷/金属复合靶板分析波阻抗对陶瓷锥形态的影响.

图2 靶板结构示意图Fig.2 Schematic diagram of the target plate
1.2 试验结果与分析
试验后回收陶瓷复合靶板,清理弹着点附近尺度较小的碎块后,呈现出清晰的陶瓷锥形貌,如图3所示,弹孔周围出现许多交叉分布的环向和径向裂纹,并形成沿环向近似均匀分布的类扇形碎块.为了获得陶瓷锥锥角的大小,以回收有效的陶瓷碎块为样本,如图4所示,通过测量各陶瓷碎块的倾角,以此获得陶瓷锥锥角β的大小.由于每组试验中所收集的陶瓷碎块锥角β的离散性较大,为了进一步分析背板材料、厚度等因素对陶瓷断裂锥锥角的影响,后续的分析采用数理统计方法进行处理,具体的统计结果如表1中所示.
图5为着靶速度为520 m/s时背板厚度与陶瓷锥锥角的大小关系.图中显示,随着金属背板厚度的增加,陶瓷锥锥角呈现出增大的状态,并与背板厚度呈线性关系,且锥角增大的趋势较为明显.

图3 试验中回收的样品径向裂纹及环向裂纹Fig.3 Radial and circumferential cracks of recovered samples in the test

图4 试验中回收的样品锥角大小Fig.4 Size of sample cone angle recovered in the test

表1 影响陶瓷断裂锥锥角各因素数理统计结果

图5 背板厚度对陶瓷断裂锥锥角的影响Fig.5 Effect of backing plate thickness on cone angle of ceramic fracture cone
为探索背板材料波阻抗对陶瓷断裂锥形成的影响,选择两种强度相近且不同杨氏模量的材料(两种材料分别为2024铝合金与Q 235钢)作为背板,进行复合陶瓷靶板的抗12.7 mm穿燃弹侵彻实验.如表2中所示,当弹体以400 m/s的着靶速度分别侵彻以铝合金和Q 235钢为背板的复合靶时,以铝合金为背板的复合靶陶瓷锥锥角明显大于以Q 235钢为背板的复合靶.为了便于分析统计,将背板材料的波阻抗做无量纲处理,同除氧化铝材料的波阻抗,得到材料波阻抗比与陶瓷断裂锥锥角的关系,如图6所示,侵彻过程中形成的陶瓷锥锥角随着界面波阻差值的增加而减小.
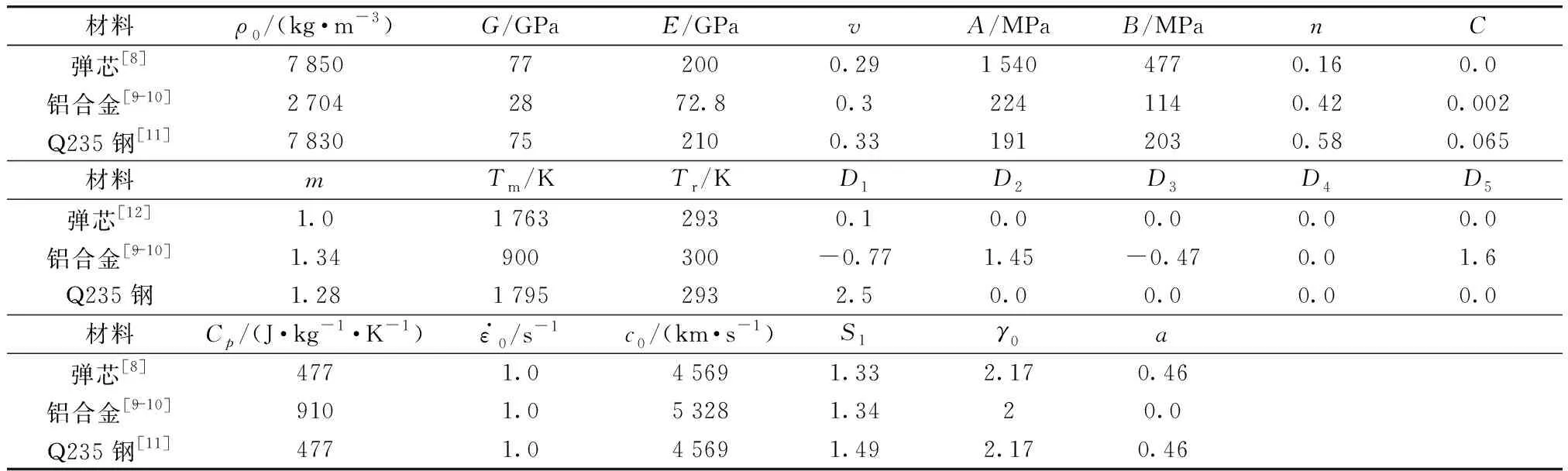
表2 钢弹芯[8]、2024铝合金[9-10]、Q235钢[11]材料模型参数及状态参数Tab.2 Material model parameters and state parameters of steel core[8],2024 aluminum alloy[9-10],Q235 steel[11]

图6 背板材料对陶瓷断裂锥锥角的影响Fig.6 Effect of backing plate material on cone angle of ceramic fracture cone
2 数值模拟
2.1 有限元模型
本文利用ANSYA/LS-DYNA动力学仿真软件对12.7 mm穿燃弹垂直侵彻陶瓷/金属复合靶时陶瓷锥形破坏面的形成过程进行数值模拟.为了减少计算量,又考虑到陶瓷锥主要是以环向裂纹为主且模型具有对称性,建立二维轴对称有限元模型,采用Lagrange网格,选择SOLID162 4节点实体单元,为了提高计算精确度并再现侵彻过程中陶瓷裂纹的生长,弹芯及金属背面板网格划分为0.01 mm×0.01 mm,陶瓷区域网格划分为0.002 mm×0.002 mm,如图7所示,经验证网格收敛.弹芯与靶板、靶板与靶板之间采用侵蚀接触算法.模型尺寸分别与实验相同.

图7 弹丸侵彻复合靶板的有限元模型Fig.7 Finite element model of projectile penetrating composite target
2.2 材料模型及参数
在计算时,弹芯、铝合金和Q235钢面背板均为金属材料,采用John-Son-Cook热黏塑性材料本构方程[7],该方程包含动态变形过程中材料的塑性硬化、应变率强化和温度软化效应.材料在大应变情况下的流动应力表示为
(1)
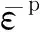
材料的失效与三轴应力、应变率和温度有关,失效应变表示为
(2)

计算所用的材料参数见表2,其中E、G、v、ρ0、Cp分别为材料的弹性模量、剪切模量、泊松比、密度和比热容;c0、S1、γ0、a为状态方程中的常数.
陶瓷材料采用JH-2材料本构方程[12],该方程主要包括对材料的强度、压力和损伤的变化关系的描述.一般陶瓷材料在达到破坏强度之前,可以按弹性材料考虑,而对于发生破坏的陶瓷材料,可以将其视为强度随损伤累积变化的完整材料.
陶瓷材料的强度包括无损伤材料的强度和完全损伤材料的强度2种,根据损伤的变化可以将含损伤陶瓷材料的等效应力表示为
(3)
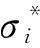

式中:A1、B1、C1、M、N为待定的材料常数;P*和t*分别为归一化的静水压力和最大拉伸静水压力,P*=P/PHEL,t*=tmax/PHEL,其中tmax为最大拉伸静水压力,PHEL为按照Mises准则由Hugoniot弹性极限(Hugoniot elastic limit,HEL)σHEL得到的静水压力.一般情况下,A1、N、t*可以通过拟合无损伤材料的压缩强度和层裂强度数据得到;C1可以通过不同应变率下的压缩破坏强度与应变率的关系求出.本文氧化铝陶瓷所用材料模型参数如表3所示.

表3 氧化铝材料模型参数及状态参数[13-15]Tab.3 Alumina material model parameters and state parameters[13-15]
2.3 仿真结果与其分析
2.3.1陶瓷的损伤演变过程即陶瓷断裂锥形成过程
以2 mm铝合金面板,12 mm氧化铝陶瓷板和2 mm铝合金背板组成的复合靶板为例,分析弹丸侵彻复合靶中陶瓷的损伤演变过程.由图8可知,在18 μs时陶瓷靶板开始出现损伤,两种裂纹分别相向延伸.在弹靶接触瞬间,冲击载荷必然在材料内部造成应力波作用,此时所产生的应力波以压缩波为主,弹着点中心区由于高压缩应力使得弹着点附近产生压剪裂纹并向陶瓷板背面延伸,裂纹扩展形成了起始破碎区.除了弹着点区域出现尺度较小的碎片外,陶瓷板背面的裂纹同时开始向陶瓷板正面延伸.压缩波从陶瓷靶板前面传播至两种不同材料构成的界面处时,由于波阻抗的差异性,入射波分解为纵向的透射波和反射波,其中反射波再与入射压力加载波随后的卸载波相互作用,在界面附近区域形成局部拉伸或剪切应力,当拉伸应力超过材料的强度,材料就会发生断裂,裂纹由陶瓷板背面向弹靶接触面扩展,形成陶瓷断裂锥.
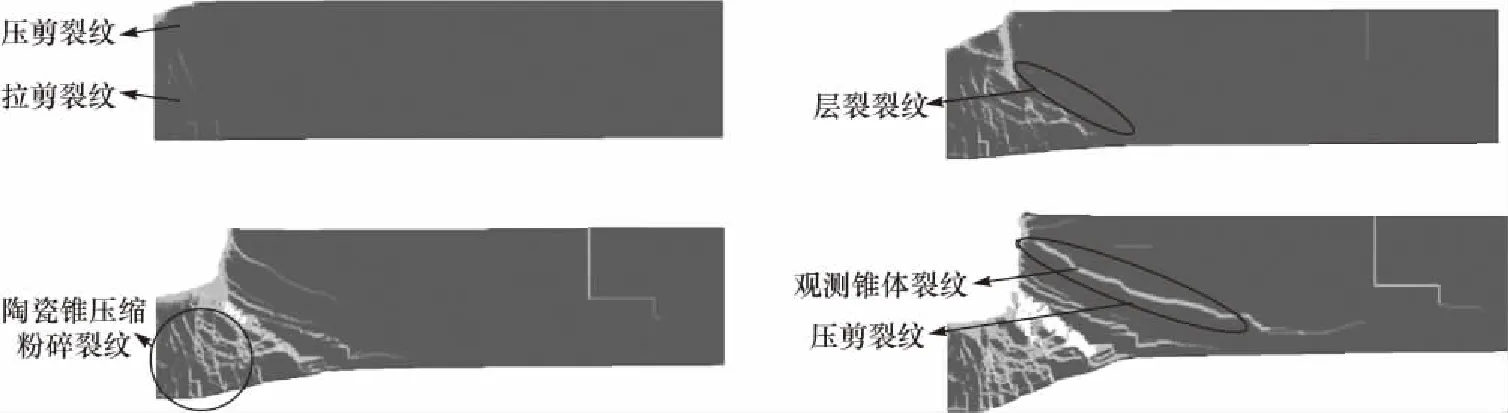
图8 复合靶中陶瓷的损伤演变过程Fig.8 Damage evolution of ceramics in composite target
在18~31 μs 时,拉剪裂纹与压剪裂纹在陶瓷厚度1/3处汇聚并贯通,形成新的自由面,之后应力波在新自由面继续发生反射形成拉伸波,进一步引起新一轮的裂纹扩展,这种过程不断循环往复的进行,从而使得层裂的现象持续发生.
在42 μs时,陶瓷锥裂纹成形,此时陶瓷板破碎损耗能量达到峰值,如图9所示,由此可知,陶瓷锥的成形在整个陶瓷抗弹侵彻过程中的能量耗散起到主导作用,这与TAN等[14]的研究结果一致.
在42~54 μs时,弹体侵入陶瓷内部,在弹体和金属背板的作用下,陶瓷锥在运动过程中受到的压缩波和金属背板反射回来的稀疏波的作用,弹体顶端的陶瓷锥不断被压馈、破碎、变小.随着时间的演化,与弹体接触一侧的陶瓷板产生大量与主裂纹几乎平行的拉剪裂纹,其中靠近弹体的裂纹不断演化,形成了可观测的锥体裂纹,即实验中回收的可观测到的陶瓷锥形裂纹.
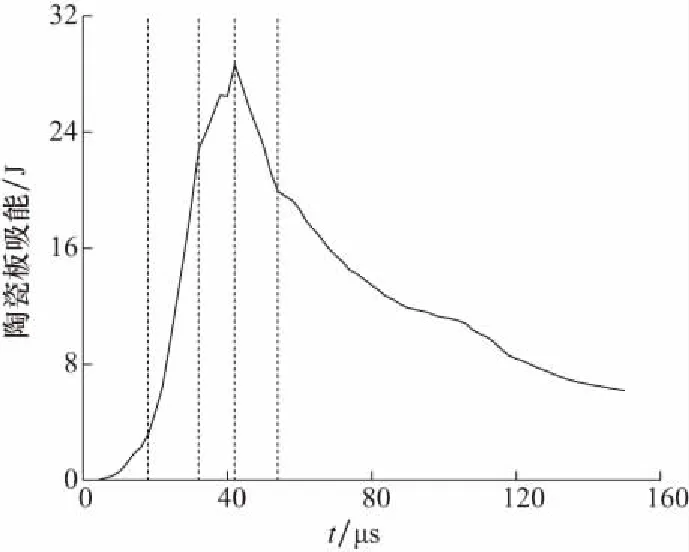
图9 陶瓷板吸能时程图Fig.9 Time-history chart of energy absorption of ceramic plate
由图10可知,形成陶瓷锥的裂纹未呈规则直线形状.早期,SHERMAN等[16]在弹体低速(≤100 m/s)冲击陶瓷靶体的实验研究中通过陶瓷上下表面圆台直径及陶瓷厚度定义了陶瓷锥锥角的大小.当弹体高速冲击陶瓷靶板时,弹着点陶瓷处出现了明显的磨蚀现象,锥形裂纹的起点不再从陶瓷的上表面开始,而是从弹坑侧边开始生长,且陶瓷锥的锥形裂纹是由压剪裂纹和拉剪裂纹贯通所形成的,其中拉剪裂纹起到了主要作用,故定义由陶瓷板背弹面开始延伸的拉剪裂纹切线与陶瓷板法线方向夹角为陶瓷锥锥角.

图10 陶瓷锥裂纹示意图Fig.10 Schematic diagram of ceramic cone crack
2.3.2不同背板厚度对陶瓷断裂锥锥角大小的影响
图11为数值仿真获得的不同背板厚度下陶瓷断裂锥锥角大小的变化趋势,并于弹道试验所测得的数据进行对比,数值模拟的结果与实验基本吻合,且误差较小,验证了模型的可靠性.
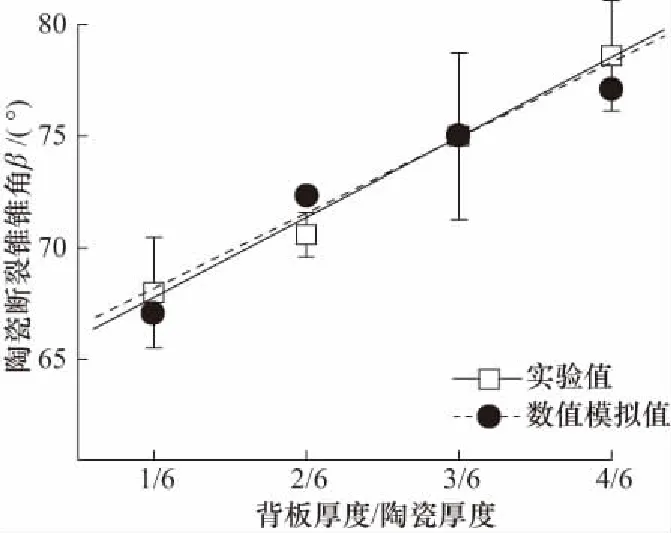
图11 不同背板厚度对陶瓷断裂锥锥角大小的数值模拟与试验验证Fig.11 Numerical simulation and experimental verification of the influence of different backing plate materials on the fracture cone angle of ceramics
图12给出了弹丸以520 m/s侵彻2 mm、4 mm、6 mm、8 mmQ235钢背板的复合靶板在70 μs时陶瓷靶板的损伤图及陶瓷断裂锥锥角大小.由此可知当背板厚度与陶瓷厚度比小于1时,厚度比每增大1/6,陶瓷锥锥角大小增加5%,即金属背板厚度越厚,陶瓷断裂锥锥角越大.从图中可知,由主裂纹所形成的陶瓷粉碎区锥角随着背板厚度的增大而增大.这是由于在陶瓷复合材料所组成的装甲结构中,陶瓷破碎的主裂纹是由弹体冲击靶板时的压剪裂纹与反射稀疏波所导致的拉剪裂纹汇聚而成的,背板厚度越大,主裂纹汇聚的交点越靠近弹靶接触面,此时拉剪裂纹的扩展起到了主要作用.而对于给定的冲击波和给定的陶瓷材料以及背板材料,由背板自由面产生的反射波强度随着背板厚度的增加而减小[17],所以背板厚度越厚,陶瓷锥破碎区的裂纹也越少.
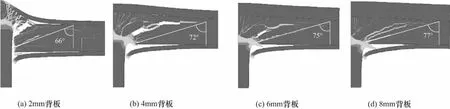
图12 不同背板厚度下陶瓷的损伤裂纹Fig.12 Damage and crack of ceramic under different thickness of backing plate
2.3.3背板材料对陶瓷断裂锥锥角大小的影响
为了进一步探究背板材料即背板波阻抗对陶瓷断裂锥锥角大小的影响,通过数值模拟建立相同侵彻条件下,背板分别以2024铝合金和Q235钢为基础定义两种不同波阻抗材料的陶瓷/金属复合装甲有限元侵彻模型.具体模型参数如表4所示.
由图13可知,当弹丸以400 m/s的着靶速度侵彻不同背板材料的陶瓷/金属复合靶时,随着界面间波阻抗之比增大,陶瓷断裂锥锥角大小随之减小,这是由于应力波在声阻抗差值较大的两界面上透射能力较弱,反射能力较强所导致的[18].与SHERMAN[19]得出的结论相符,当背板材料为低波阻抗材料时,剥落的锥形裂纹是由陶瓷/背板界面间反射的稀疏波所主导引起的结果.当背板为高阻抗材料时,应力波会从背板的自由面透射出来,从而减少了对陶瓷的损伤,所以其陶瓷锥锥角较小.此外,当波阻抗差值较小时,如图14所示,其完整陶瓷锥裂纹起源位置位于陶瓷板中部,这是由于侵彻初期高压缩应力所导致的由弹靶接触面向下传播的多重裂纹及弹体对碎裂的陶瓷的侵蚀,且此裂纹最终与反射稀疏波所形成的裂纹汇聚形成最终的陶瓷破裂锥.而当波阻抗差值较大时,界面反射回来的稀疏波相对较强,裂纹的形成主要以应力波在介质表面反射所形成的拉伸应力为主,形成拉剪裂纹并迅速呈现出完整的陶瓷锥角.
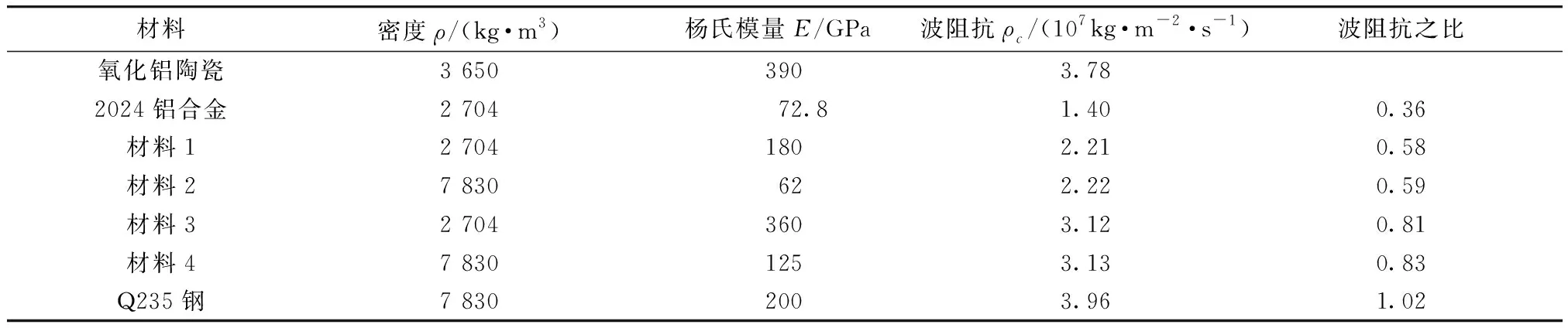
表4 不同背板及陶瓷的波阻抗

图13 背板材料对陶瓷断裂锥锥角大小的影响数值模拟与试验验证Fig.13 Numerical simulation and experimental verification of the effect of different backing materials on the cone angle of ceramic fracture cone
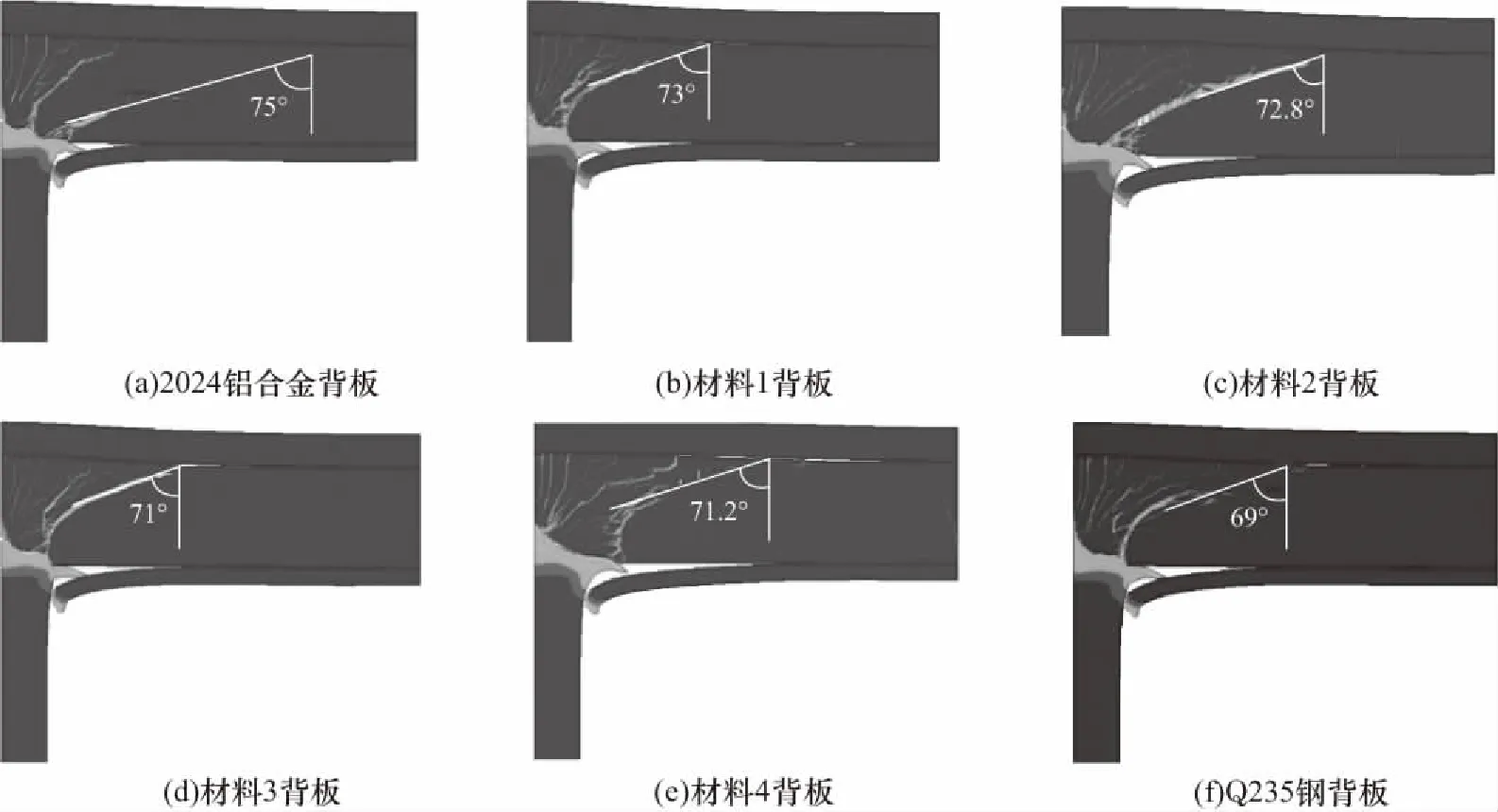
图14 不同背板材料下陶瓷的损伤裂纹Fig.14 Damage cracks of ceramics under different backing materials
3 结束语
通过12.7 mm穿燃弹的弹道实验与数值模拟,对不同背板条件下的陶瓷/金属复合靶板进行动态冲击加载,研究了背板厚度、背板材料对陶瓷/金属复合薄靶板中陶瓷锥的大小与形态的影响规律.当背板厚度增大时,背板自由面产生的反射波强度随之减小,主裂纹汇聚的交点靠近弹靶接触面,此时拉剪裂纹的扩展起到了主要作用.当背板厚度与陶瓷厚度比小于1时,厚度比每增大1/6,陶瓷锥锥角大小升高幅度在5%;当界面间波阻抗差值增大即背板材料波阻抗减小时,从界面反射的应力波增强,从而增大了对陶瓷的损伤,陶瓷断裂锥锥角大小也随之增大,此时裂纹的形成以拉剪应力为主.

