单点腐蚀船体板剩余疲劳寿命的数值计算

王慧婷，王 金，张岳林，侯志楠

(1.中国人民解放军 91404 部队，河北 秦皇岛 066001；2.海军装备部驻上海地区军事代表局驻上海地区第一军事代表室，上海 201913；3.同济大学 建筑工程系，上海 200092)

0 引 言

海水的温度、溶氧、盐度、PH 值、流速和微生物附着等因素使海洋环境成为强腐蚀性环境[1]。船体结构长期在海洋环境中服役，腐蚀不可避免。腐蚀造成船体板厚度减小，破坏结构完整性，最终导致结构失效，从而成为影响船体结构寿命的主要因素。挪威船级社（DNV）将腐蚀类型分为均匀腐蚀、点腐蚀、沟槽腐蚀和边缘腐蚀[2]。其中，由于点腐蚀会造成结构的应力集中[3–4]，所以破坏性比均匀腐蚀更大，且由于点腐蚀蚀坑形状不规则、分布不均匀，所以点腐蚀结构的剩余强度计算更为复杂。因此，近年来，对腐蚀结构剩余承载能力的研究正在从均匀腐蚀向点腐蚀转变[5]。Khedmati 等[6–7]对含双面随机分布腐蚀的钢板的单轴压缩强度进行了计算，并将双面随机腐蚀钢板在单轴压缩下的非线性弹-塑性平均应力-应变关系与无腐蚀钢板进行了对比。Soares 等[8]对严重腐蚀箱型梁的极限强度进行了试验评估，并研究了含部分深度蚀坑的方板在单轴载荷下的极限承载能力[9]。

对于腐蚀钢板的剩余强度计算，除了考虑腐蚀自身，还应计及焊接残余应力及初始缺陷等因素。Soares等[10]评估了含初始缺陷腐蚀钢板极限强度的特征值，研究了腐蚀程度对钢箱型梁极限强度的影响[11]，并分析了承受腐蚀和维修船体结构的可靠性[12]。点腐蚀蚀坑的分布是随机、不均匀的，文献[13–14]中的计算考虑了局部腐蚀的随机性。除了压缩强度[15–16]外，Soares 等还对腐蚀小尺度试件的拉伸强度进行了评估[17]。

腐蚀钢板极限强度随各影响因素变化关系的曲线拟合也是该领域的研究热点。Paik 等[18]通过计算结果的回归分析拟合了点蚀板在剪切作用下极限强度的闭合形式设计公式。Soares 等[19]提出了预报点蚀软钢板在双轴压缩下极限承载能力的闭合形式公式。张岩，黄一等分别对点蚀钢板在单轴压缩[20–22]、双轴压缩[23]和组合载荷[24]下的极限强度随腐蚀体积的变化关系进行了拟合。

综上所述，学者们对腐蚀船体结构的剩余强度进行了大量研究。然而，由于波浪载荷为交变载荷，所以只考虑极限强度是不够的，必须计及疲劳对腐蚀船体结构剩余寿命的影响。本文建立了含圆柱形蚀坑船体板的有限元模型，通过与弹性力学解析解的对比对网格类型进行了选择，对单点腐蚀船体板剩余疲劳寿命进行计算，研究蚀坑直径和蚀坑深度对单点腐蚀船体板疲劳寿命的影响。最后，对船体板剩余疲劳寿命-蚀坑深度曲线进行了拟合。

1 研究对象

本文的研究对象为200 mm×200 mm×10 mm 的方板，其中心含一圆柱形蚀坑，深度为h，直径为d，如图1 所示。薄板一端固定，另一端承受在一个工作循环内承受P=250 MPa，−250 MPa 交替变化的单轴拉/压载荷。为了使应力计算容易收敛，先在模型上施加50 MPa载荷，在疲劳分析中再将载荷缩放至250 MPa。材料牌号为SAE-950C-Manten，弹性模量E=2.03×1011Pa，泊松比u=0.3，密度ρ=7.85E−9t/mm3。

图1 研究对象的几何模型Fig.1 Geometry of the subject

2 网格类型的选择

张岳林等[3]认为：在一般静力学分析中，网格类型对计算结果的影响很大。本文以d=10 mm，h=10 mm的情况为例，选择3 种不同类型的网格，3 种工况下孔边应力集中系数与弹性力学解析解的对比如表1 所示。

表1 不同网格类型的计算结果Tab.1 Calculation results of different grid types

可见，使用线性单元计算误差较大，而使用C3D20网格计算的孔边应力集中系数与解析解误差较小。因此，本文后续计算均使用该类型网格。

3 结果与讨论

以d=10 mm，h=5 mm 的情况为例，使用Abaqus 进行应力计算，Fe-Safe 进行疲劳寿命计算。蚀坑区域的网格进行了加密，网格总数为779，如图2 所示。

图2 网格的划分Fig.2 Mesh of the subject

经计算，含d=10 mm，h=5 mm 蚀坑的船体板在单轴拉伸载荷下的应力分布如图3 所示，剩余疲劳寿命（循环次数）如图4 所示。可见，最危险位置为蚀坑边缘应力最大位置，剩余寿命为103.693=4 931.738 04次；剩余寿命最大位置为应力最小位置，剩余循环次数为107.313=20 558 905.96 次。

图3 应力云图Fig.3 Stress distribution

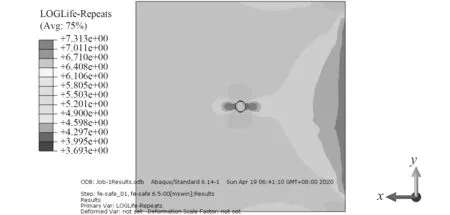
图4 剩余疲劳寿命（循环次数）Fig.4 Residual fatigue life(Cyclic number)

图5 为给定循环次数下结构能承受的载荷图，它代表要想使整个结构的剩余疲劳寿命达到1E7 次，须将载荷缩小0.495 3 倍。

图5 载荷缩放系数Fig.5 Load scale factor

3.1 蚀坑直径的影响

为了研究蚀坑直径对含圆柱形蚀坑船体板剩余疲劳寿命的影响，设计了d=10，20，30，40，50mm 共5 组仿真试验。经计算，船体板最危险位置疲劳寿命随蚀坑直径的变化如图6 所示。可见，当蚀坑深度大于板厚的一半时，含圆柱形蚀坑船体板的剩余疲劳对数寿命随蚀坑直径的增大而增大，两者之间基本上是线性关系。

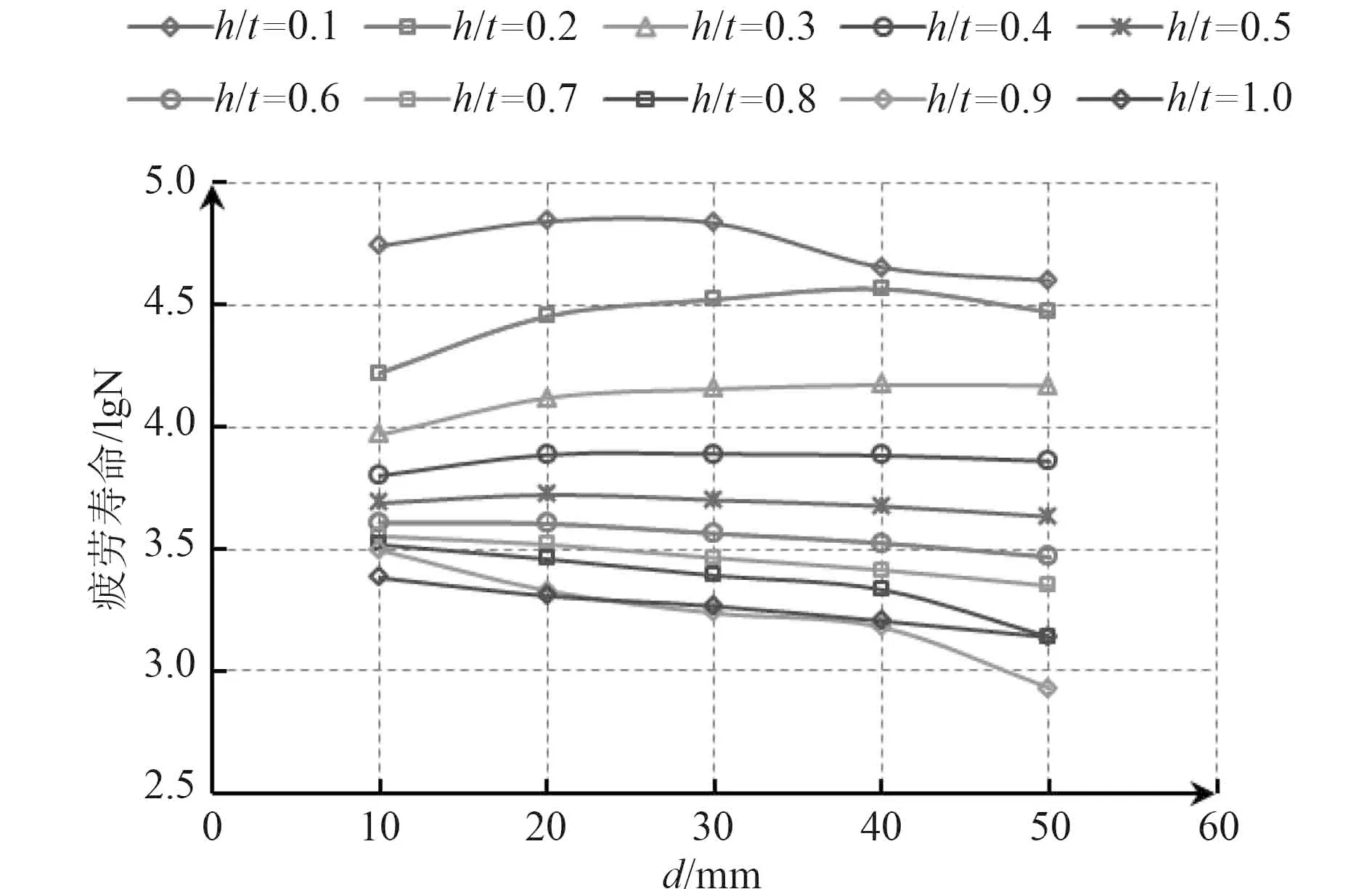
图6 船体板疲劳寿命随蚀坑直径的变化Fig.6 Fatigue life of the bull plat evs.diameter of the pit

3.2 蚀坑深度的影响

为研究蚀坑深度对船体板疲劳寿命的影响设计了h/t=0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1 共10 组仿真试验。经计算，含圆柱形蚀坑船体板剩余寿命随蚀坑深度的变化如图7 所示。可见，船体板危险位置剩余寿命随蚀坑深度的增大而减小，尤其是当蚀坑深度小于板厚的一半时，船体板疲劳寿命随蚀坑深度的增大迅速减小；当蚀坑深度大于板厚的一半时，船体板疲劳寿命随蚀坑深度的增大而减小的速度降低，两者之间基本上呈线性关系。另外，对比图6 和图7 可以发现，相对于蚀坑直径，蚀坑深度对船体板剩余寿命的影响更为显著。

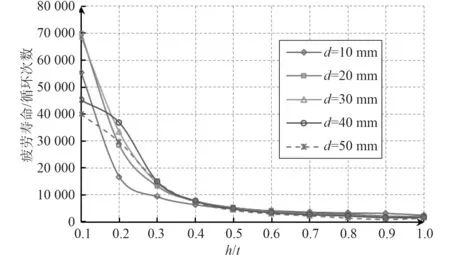
图7 船体板剩余寿命随蚀坑深度的变化Fig.7 Residual life of the hull plate vs.depth of the pit

3.3 含蚀坑船体板疲劳寿命的经验公式

由上文可知，相对于蚀坑深度，蚀坑直径对含圆柱形蚀坑船体板剩余疲劳寿命的影响较小，故可以忽略蚀坑直径的影响，对船体板疲劳寿命-蚀坑深度曲线进行拟合。该曲线与倒指数曲线相似，可用最小二乘法对其进行拟合，先将倒指数曲线变换为线性曲线，令y'=lny，x'=1/x，得y'=lna+bx'。其法方程的系数矩阵及常数如表2 所示。

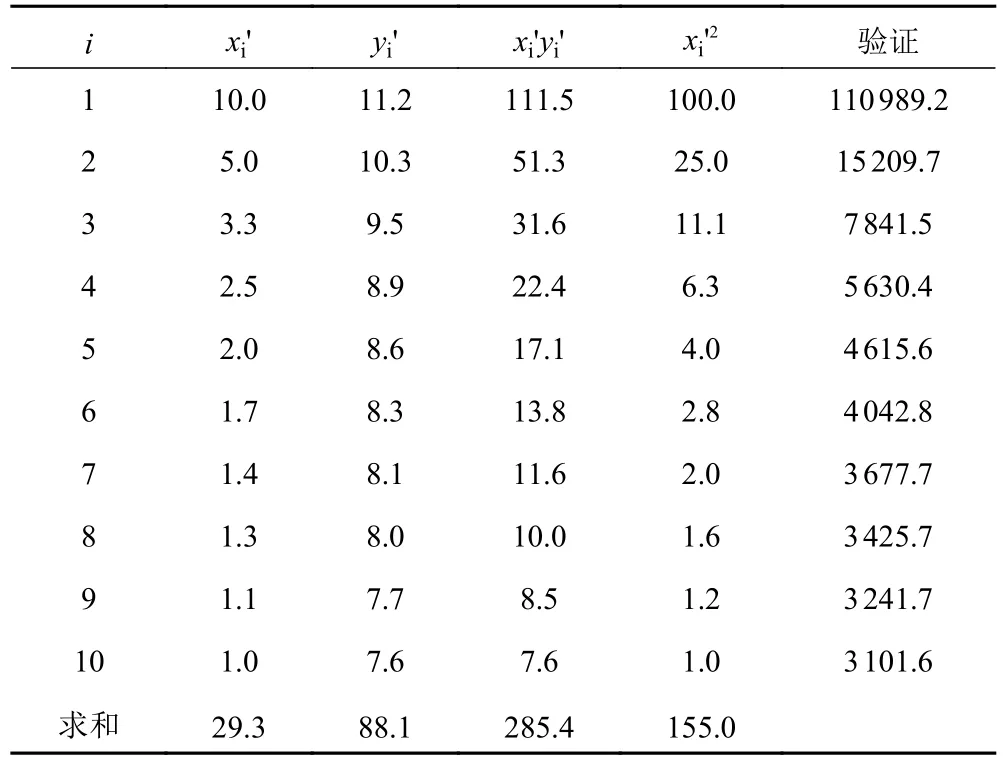
表2 倒指数函数拟合的系数矩阵与常数Tab.2 Coefficient matrix and constant of inverse exponential function fitting

当用幂函数曲线进行拟合时，令y'=lny，x'=lnx，其法方程系数矩阵及常数如表3 所示。2 种函数拟合结果分别如式（1）和式（2）所示。2 种函数的拟合曲线值见表2 和表3，可见，用幂函数作拟合曲线较好。

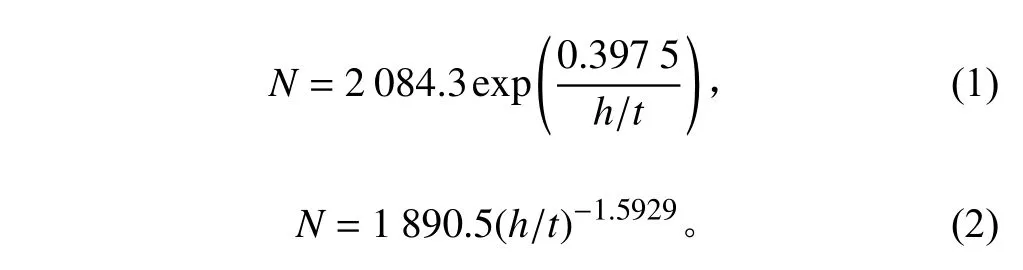
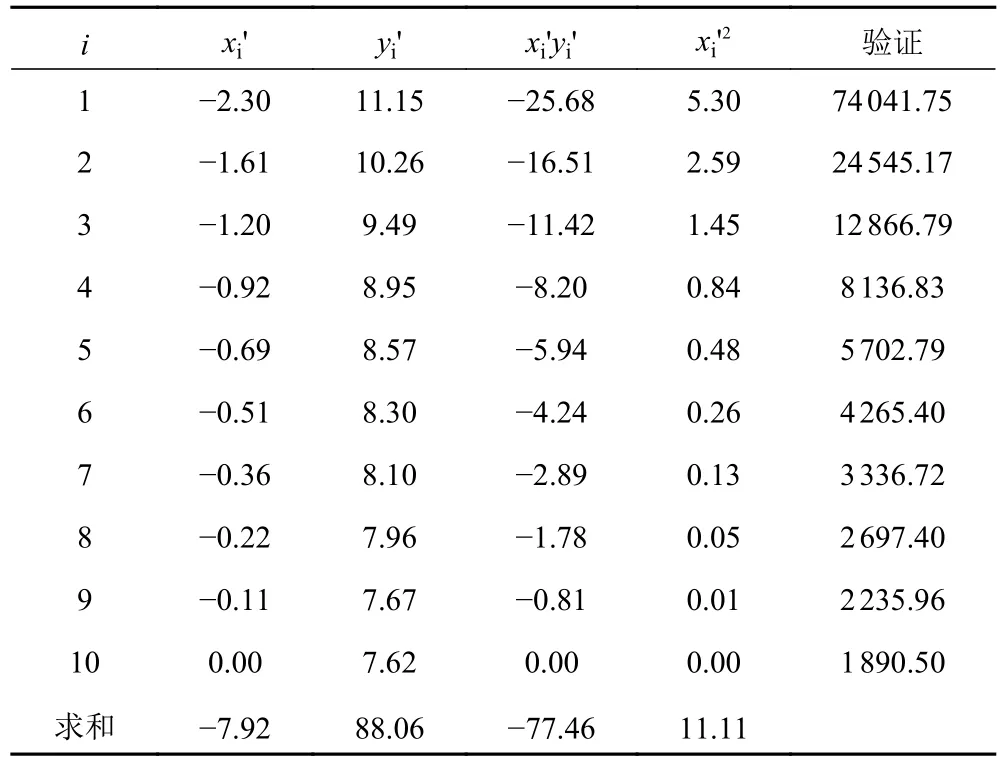
表3 幂函数拟合的系数矩阵与常数Tab.3 Coefficient matrix and constant of power function fitting

4 结 语

本文建立含圆柱形蚀坑船体板的有限元模型，通过与弹性力学解析解的对比对网格类型进行选择，对单点腐蚀船体板剩余疲劳寿命进行计算，研究蚀坑直径和蚀坑深度对单点腐蚀船体板疲劳寿命的影响。最后，对船体板剩余疲劳寿命-蚀坑深度曲线进行了拟合。根据本文的研究，可得到如下结论：

1）对于点腐蚀钢板的应力集中计算，使用而此单元比使用线性单元更准确。

2）含圆柱形蚀坑船体板剩余疲劳寿命随蚀坑深度的增大而迅速减小；蚀坑直径对船体板疲劳寿命的影响不大。

3）使用幂函数对船体板疲劳寿命-蚀坑深度曲线进行拟合比使用倒指数函数更准确。