基于线性动态规划的管材切割最优使用率优化研究
姬玉生 丁龙斌 郑晓芳 白旭光 姜杨杨 尹高冲 李悦


摘 要:当前轨道车辆管材切割技术,存在多种管路长度尺寸并存,无法通过一定手段获取最优管材切割尺寸分配和最优使用率的情况。本文设计了一种线性动态规划的求解思路,首先使用動态规划算法算出所有单根管材可能的管路尺寸分布,然后将其作为系数矩阵构建线性方程,利用线性规划算法求出最优解,最后利用One-hot算法将最优解映射到最优的管路尺寸切割分布上。设计并实现了基于该算法的GUI,能够满足生产中的使用,有效提升了管材切割尺寸的计算效率,并能在一定程度上节约管材,降低生产成本。
关键词:管材切割 最优使用率 动态规划 线性规划 One-Hot GUI开发
中图分类号:TG385 文献标识码:A文章编号:1674-098X(2021)04(b)-0066-04
Research of Optimal Utilization of Pipe Cutting Based on Linear-Dynamic Programing
JI Yusheng DING Longbin* ZHENG Xiaofang BAI Xuguang JIANG Yangyang YIN Gaochong LI Yue
(CRRC Qingdao Co., Ltd., Qingdao, Shandong Province, 266111 China)
Abstract: In the current rail vehicle pipe cutting work, there are a variety of pipe lengths and sizes coexist, and it is impossible to obtain the optimal pipe cutting size distribution and optimal utilization rate through a certain means. This paper designed a kind of linear dynamic programming to solve the train of thought, all will be the first to use dynamic programming algorithm of single pipe may pipe size distribution, and then use it as a coefficient matrix to construct linear equation, using the linear programming algorithm to find the optimal solution, and finally using one - hot algorithm to map the optimum solution to optimal cutting line size distribution. The GUI based on the algorithm is designed and implemented, which can meet the requirements of production, effectively improve the calculation efficiency of pipe cutting size, and to a certain extent, save pipe material and reduce production cost.
Key Words: Pipe cutting; Optimal utilization; Dynamic programming; Linear programming; One-Hot; GUI development
轨道车辆的制动和给水装置大多使用管路送风给水,部分电路也通过管路保护电线,管路的管长、管径等参数各有不同。在当前的管材切割工艺中,需要根据下料表将不同长度的管料在一根较长的管材上面切割出来,当管料较多时,所需要的管材数量各有不同。此时,由于存在锯片厚度、最小前端余量和最小后端余量,在每根管材切割不同的管料时,需要的管材数量可能不同,管材所能够达到的使用率也有所差异,造成管材和运输成本的增加。
本文提出了一种基于动态规划和线性规划的最优管料长度切割方案,确保在给定前后余量和锯片厚度条件下,管材数量达到最少,管材使用率达到最高,提升管路切割的效率,降低成本。
1 最优管路切割方案
最优管料长度切割方案是指,在管材总长度L一定的情况下,去除前端端部的规定最小余量长度m1,后端端部最小余量长度m2,锯片厚度造成的损失N,切割出尺寸为的k根管料时,使管材使用数量n最少、管材使用率μ最高的方案。对于第i根管路,μ的计算方法如公式(1)所示:
(1)
其中,μi为第i根管材的使用率,ki为第i根管材要切割出的管料数量。
单根管材的实际使用长度l为公式(2):
l=L-m1-m2-(ki+1)*N(2)
为最大化l,上式可化为式(3):
∑(li+N)≤L-m1-m2-N(3)
式中,l为管材实际使用的长度,li为管材上下料管路长度,N为锯片厚度。
对于多根管材的管路切割方案,对于多个管料长度的多种可行状态组合,对应着不同的管材利用率,因此需要选取合适的工作方案,使多根管材在整体上达到最优的利用率。该问题可描述为可迭代的多级决策的最优问题,对于多级决策的最优问题可利用动态规划解决,即对单根管材选择的最佳切割方案,而这里多根管材组成了一个整体系统,局部最优并不保证是全局最优,因此有必要对动态规划算法进行改进,使其能够满足多管材条件下的最优化问题[1]。
1.1 动态规划求解单根管管材切割方案
动态规划(Dynamic Programming,DP)是运筹学的一个分支,是求解决策过程最优化的过程。20世纪50年代初,美国数学家贝尔曼(R.Bellman)等人在研究多阶段决策过程的优化问题时,提出了著名的最优化原理,从而创立了动态规划。动态规划的应用极其广泛,包括工程技术、经济、工业生产、军事以及自动化控制等领域,并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解[2]。
在使用动态规划算法前,需要首先确定系统的目标函数、控制变量和状态变量。在本文中,由公式(3)可得目标函数可表示为公式(4):
(4)
设定两个状态量,当前管路所使用长度方案下的管路下料集合,控制变量为最大管路可使用长度 ,应满足公式(5):
(5)
状态量的更新方程为公式(6):
(6)
在優化过程中,需要为该问题添加可行性约束,其主要包括管材可使用长度、管路数量等,如公式(7)所示:
(7)
其中,为方案中第i中管料长度的个数,为总体中相同管料长度的个数。
根据状态方程求解,将符合约束条件的所有可能管路的数量组合储存为一个长度为k的向量中,k为总体中不重复的管路个数。最后,将这些向量合并为一个k*n矩阵M,n为所有可能的方案数量。
1.2 线性规划求解总体最优切割方案
线性规划(Linear Programming 简记 LP)是了运筹学中数学规划的一个重要分支。自从1947年G. B. Dantzig提出求解线性规划的单纯形法以来,线性规划在理论上趋向成熟,在实用中由于计算机能处理成千上万个约束条件和决策变量的线性规划问题,线性规划是现代管理中经常采用的基本方法之一[3]。
在动态规划得到的k*n维矩阵M中,每一列为单根管材可能采用的方案,记为,每一行为固定长度的管路在各个方案中的数量,记为。在总体中的固定长度管路数目记为。为使管材使用率最高,管材使用数目满足最少且满足管路生产需要的条件,即所需要的管路全部完成切割。此时,设每根管材可采用的方案ci对应的方案数量为xi,则该优化问题可描述为公式(8):
最小化:(8)
在优化过程中,需要为该问题添加可行性约束,使最后的结果满足该问题中的约束条件,主要包括切割出的管料数目需要大于或等于所需要的数目,且各个方案的个数为整数。如公式(9)和公式(10)所示:
服从条件:
(9)
(10)
求解该问题,即可得到满足给定条件的最优管材数目和此时管材的切割方案。
1.3 One-Hot 映射求解可用最优方案
One-Hot编码,又称为一位有效编码,主要是采用N位状态寄存器来对N个状态进行编码,每个状态都有独立的寄存器位,并且在任意时候只有一位有效。One-Hot编码是分类变量作为二进制向量的表示,这首先要求将分类值映射到整数值。然后,每个整数值被表示为二进制向量,除了整数的索引之外,它都是零值,被标记为1。
当得到最优管材数目和管材切割方案后,由于条件给定的管路数目大于等于给定的数目,因此还需要将所得的方案映射到满足问题给定数目的方案中,且保持尽可能多的管材使用率。基本的解决思路是在使用率低的管材方案中将多余的管路去除,即可满足要求。为解决这一问题,记管材切割方案为矩阵 P,每一行为一根管材的方案ci,每一列为固定长度管路在方案中的数量nj,管路冗余量residual如公式(11)所示:
(11)
对冗余量residual作one-hot编码,将其化为每一个样本只含有一个1的向量形式hj。然后,将cj与每个residual的向量求欧几里得距离,如公式(12)所示:
(12)
当di最小时,有ci与residual的距离最小,说明修改该方案能够尽量保证其他方案不变,即可保持尽可能多的管材使用率。迭代运算,直到residual中的剩余量全部为0。
2 GUI程序设计
2.1 最优管材切割方案算法实现
本文选用Python编程语言实现,版本为3.5.1。使用模块有数学科学计算工具包numpy,线性规划模块pulp. 算法共分为3个模块,分别为动态规划模块,线性规划模块和最后的one-hot修正模块[4-5]。
动态规划模块主要包括weights、nums和max_weight三个输入值,分别表示下料管路的长度、下料管路的个数和最大管材使用长度。在最大管材可使用长度之内,对下料管路长度进行编辑,将所有满足条的管路长度组合保存到weight_num中,最后返回该值,即得到所需要的所有可能的管路组合方案。动态规划模块的代码如图1所示。
线性规划模块包括动态规划得到的可能的组合方案weight_num,将其映射为线性规划中的num_arrs,以及各类下料管路个数nums,部分代码如图2所示。首先将num_arrs转换为矩阵形式(k*n维矩阵M),然后依据公式(8)建立线性规划问题描述,依据(9-10)建立线性规划问题的约束条件,然后计算得出可能存在的结果。结果输出后,将公式(8)中非零的xi取出,作为获得的问题的解。
在线性规划得到所有方案选择出的个数组合之后,利用one-hot算法和公式(11)计算出residual,并利用公式(12)迭代计算,直到residual为0,此时的init即为全局最优解,即最优管材切割方案,如图3所示。
2.2 最优管材切割方案GUI设计与实现
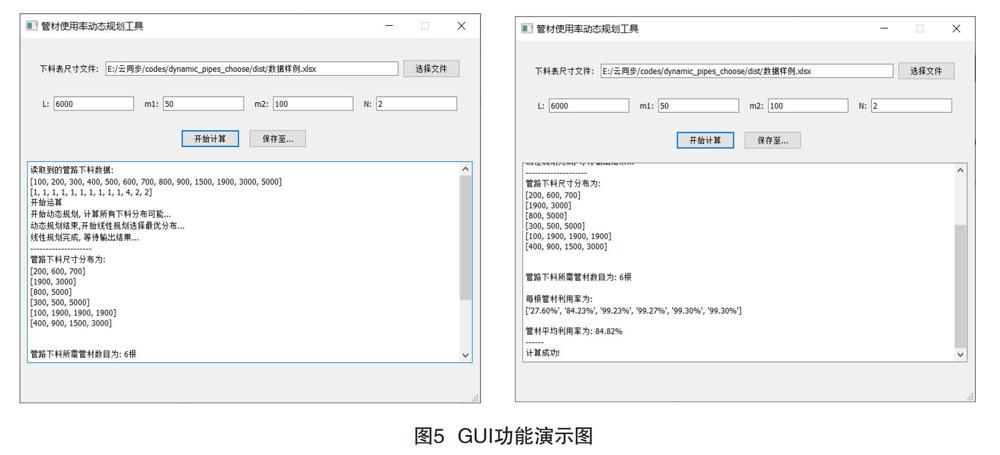
为方便班组人员使用,本文设计了人机交互界面(GUI)供给其他人员使用。如图4所示,该图为本文的GUI实现图,主要包含4个功能:从文件中取出下料管路的尺寸和数量;输入管材长度L、头部最小余量m1、尾部最小余量m2和锯片厚度N;当点击开始计算后,在下方的嵌入显示界面显示计算过程和计算结果;最后点击保存可将计算结果保存到选择的文件中。
图5为该GUI应用程序的功能描述图,当选择了读取的文件后,将在下方显示界面实时显示读取到的文件数据;点击开始计算后,程序会将计算的中间过程和计算结果实时显示在界面,包括一些出错信息等。
3 结语
本文运用Python语言设计和实现了基于线性动态规划的管材切割最优方案选择工具,该工具结合了一线管路弯管工作的生产实际,通过对管路下料选择的数学理论进行研究,利用动态规划、线性规划的优化选择算法实现了最优方案选择的功能,利用Python编程语言和科学工具包numpy,将其用编程语言实现,然后利用Qt编写GUI提供给用户使用,并添加了多种特殊情况判断,能够满足生产中的使用,有效提升了管材切割尺寸的计算效率,并能在一定程度上节约管材,降低生产成本。
今后,可在本文研究的基础上,继续深入,进一步将该解决方法应用到其他类似的场景如地板铺设、原材料尺寸选择等等。此外,针对其他问题,也可结合本次设计,选择其他相似的优化算法进行优化,以提高生产效率,提质增效[6]。
注:软件源代码可在https://github.com/dlb123/dynamic_pipe_choose获取
参考文献
[1] 俞山青,郑钧,殳欣成,等.一种真假信息传播能力评估的动态规划算法[J].小型微型计算机系统,2021,42(1):85-90.
[2] 何洪文,石曼,曹剑飞,等.基于动态规划的再生制动能量管理策略[J/OL].重庆理工大学学报:自然科学:1-8[2021-01-25].http://kns.cnki.net/kcms/detail/50.1205.t.20201222.1324.004.html.
[3] 黄红,顾炜江.基于线性规划模型的人力调配管理智能优化系统设计[J].现代电子技术,2021,44(2):135-139.
[4] 丁龍斌.随机森林入侵检测算法研究[D].兰州:兰州交通大学,2020.
[5] 苏佳丽,伍忠东,丁龙斌,等.基于IGWO-RBF的LTE-R切换算法研究[J].计算机工程与应用,2020,56(8):74-80.
[6] 丁龙斌,伍忠东,苏佳丽.基于集成深度森林的入侵检测方法[J].计算机工程,2020,46(3):144-150.

