消防体系中双目摄像机特征点提取算法浅析

许继阳

（大庆油田信息技术公司规划设计中心，黑龙江 大庆 163000）

0 引 言

利用视频技术对大空间建筑展开消防监控，需要将双目摄像机获取到的图像数据进行分析处理，从而确定火灾发生点。双目摄像机的优势在于能够从不同的视角对目标物体进行数据获取，而普通摄像机只能产生平面数据，只能提供方向数据，无法提供距离数据。双目摄像机能够实现从二维图像到三维空间的映射。在这个数据处理和映射的过程中，特征点的提取是重要根基之一。当火灾发生时，系统会首先对火源图像进行预处理，提升匹配精度，而后展开特征点的提取和匹配。该领域存在多种算法，应用比较广泛的是尺度不变特征变换（Scale Invariant Feature Transform，SIFT）特征点算法以及其他在此基础上改进的算法，都是相关研究人员关注的重点[1]。

1 SIFT算法原理分析

SIFT算法于2004年由M.Brown和D.Lowe等人提出。严格来说，这也是一种改进算法，其核心思想是利用高斯差分在图像中计算出极值点，进一步将对比度偏低以及不稳定的极值点剔除，其以极值点的邻域梯度作为主方向[2]。SIFT算法首先假设数字图像I(x,y)的尺度空间函数为：

式中：等式右侧第一个部分G函数为二维高斯函数；σ为尺度因子。则高斯函数的表达式为：

对于极值点的计算，首先将原始图像以s倍变化距离进行采样，建立图像分层结构。而后依据式（1）对图像的每一层用不同尺度因子的高斯函数计算卷积，得到数字图像的高斯金字塔，每一层高斯函数的尺度因子变化保持k倍。对于一个卷积目标来说，可以用不同尺度的高斯函数的差和输入的图像对其进行卷积，则会进一步形成数字图像的高斯差分方程：

高斯函数的卷积差能够加速局部极值点的获取速度。但是获取到极值点之后，还必须确保其能够保持稳定。为此，需要将样本像素点放在立体邻域中进行非最大值的抑制。具体来说，要将中心点与其周围的18个相邻像素点展开比较计算，确定出新的极值点并进行标记[3]。

之后，SIFT算法需要剔除不稳定的特征点，也就是对于上述获取到的极值点进行判断和剔除，主要是将对比度比较低的点和处于边缘的特征点剔除。

对于对比度比较低的点的剔除，首先在已经获取到的极值点处对尺度空间的生成函数进行泰勒展开。在精度允许的情况下忽略高次项，可以获取到：

式中：X=(x,y,σ)T为样本点偏移标记。可以进一步从式（4）获取到极值点位置：

如果由式（5）获取到的值大于0.5，则可以认为偏移量极值与其他样本点接近，可以用插值代替这个样本点，获取到插值估计值：

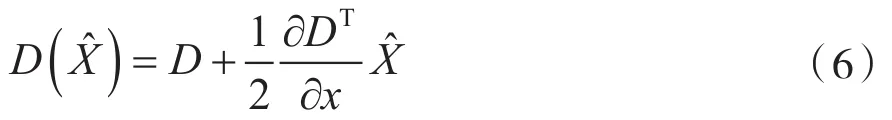
在剔除边缘特征点时，通常以极值点作为中心对其邻域展开采样，进一步通过式（7）和式（8）来计算样本点的梯度和方向：

进一步将特征点作为中心，对周围方向上的像素梯度进行计算。每间隔10°选取一个方向，共计36个方向。获取到的像素梯度值最大的方向，定为该极值点的主方向。如果存在多个相近值，则该极值点具有多个方向。

在SIFT框架下，特征点描述需要首先将描述子坐标调整到同特征点一致的位置上，并且以特征点作为中心，对其16×16个像素展开高斯加权，并且将其划分到4×4像素大小进行采样。每个样本包括8个方向信息，对应地可以获取到特征点的128维向量描述。

2 SURF算法以及原理分析

SURF算法是在SIFT算法基础上提出的，在速度和鲁棒性方面表现更优，尤其可以改善SIFT算法在面对大量数据时耗时过长的问题。SURF算法于2006年由Bay等人提出，能够保持对数字图像的平移、旋转具有不变性，而且环境中的噪声也能表现出很好的鲁棒性。总体来说，SURF算法的实现可以分为特征点检测和特征描述两步。具体来说，首先对图像积分，而后与方框滤波进行卷积，获取到Hessian矩阵，并且将每个点都与其相邻位置和相邻尺度上的Hessian值展开比较，最终获取到极值点[5]。

在图像积分环节，SURF算法通过积分在原始图像的基础上获取到新的图像。新的图像上的像素点，其值为原图上对应点与原点组成的矩阵区域的像素值之和。这个环节是SURF能够实现快速运算的根本所在。

对于原始图像上的某一点p(x,y)而言，p的积分图像可以用式（9）进行表达：

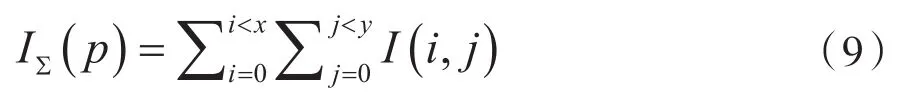
式中：I(i,j)即为对应点的像素值。通过对原始图像进行积分，原始图像中的任何一个矩形区域的像素都可以通过加工之后图像上的像素加减获取到。在此基础之上，SURF进一步用方框滤波器的方法展开特征点检测，来实现对于高斯函数的近似代替。

在SURF计算体系下，图像尺寸保持一定，通过对图像进行分层，建立起图像尺度空间，在不同的空间上展开特征点的检测[6]。具体来说，维持原始图像不变，用方框滤波器的大小对积分图像展开滤波，并且获得图像的尺度空间。之后仍然用Hessian矩阵进行特征点的计算，对图像进行积分，并且建立起图像的尺度空间，针对空间上每一层图像用Hessian矩阵计算极值点。对于图像中的任一点(x,y)，有对应的尺度空间，其尺度标记为σ，则Hessian矩阵为：

式中：Lxx、Lyy以及Lxy分别为对应像素点和高斯滤波二阶偏导卷积的计算结果。如果用方框滤波模板和原始图像的卷积对其进行近似代替，即将初始方框滤波器与σ=1.2的高斯二阶偏导近似，则Hessian矩阵行列式变换为：

式中：Dxx、Dyy以及Dxy分别表示上述用来近似代替Lxx、Lyy以及Lxy的卷积；并且将权重系数记为，通常取值0.9。而后对Hessian矩阵行列式进行计算，当其超过限定阈值时，则可以确定该点是否为极值点，方法同样是将该点与邻域8个点以及空间环境中的18个点进行非极大值抑制，如果该点比其邻域中的点响应值都大，则可以确定该点为特征点。而后进一步进行空间插值，获取特征点的具体位置和尺度值。

完成上述工作之后，即可展开特征点描述，具体包括两个环节的主要任务。

第一，需要计算特征点主方向。这主要是为了落实特征点匹配具有旋转不变性的特征，即要求以上面已经获取到的特征点作为中心，以6 s这一尺度值作为半径的区域中，计算像素点在x和y两个方向的哈尔小波响应值，并且依据欧氏距离给出对应的权值系数，对响应值进行加权计算且进一步采用直方图统计。以特征点作为中心，从x轴方向开始，对区域内60°范围内的哈尔小波响应值求和，获取到一个新的矢量，而后每5°重复该操作，获取到一个包含有72个矢量的群落，该群落中最长矢量方向即标记为该特征点的主方向。

第二，展开特征向量的确定。与SIFT算法类似，通过上述操作能够获取到两幅图像的特征点及其位置和尺度值。要正确匹配特征点，还需要进一步对其展开描述，这是有效提升特征点匹配率的重要环节。然而，SURF和SIFT两种算法仍然存在很大差异。SURF算法以特征点作为原点并且选择其周边邻域，将该区域内图像主方向旋转到与特征点一致的角度，进一步将该邻域划分成为16个子区，每个区大小约为5 s×5 s，计算图中每个像素点在x和y轴两个方向上的哈尔小波响应值，分别记为dx以及dy，对该结果进行高斯加权来增加特征点鲁棒性。之后对区域内所有点的响应值求和，分别记为Σdx和Σdy，进一步对其绝对值进行求和，分别标记为Σ|dx|和Σ|dy|，即可以与前述两个值形成4维描述向量，即（Σdx，Σdy，Σ|dx|，Σ|dy|）。则 16 个子区会产生一个16*4的特征描述向量。

从这一计算过程可以看到，SURF算法利用积分特征来实现运算速度的有效提升，既保持了尺度不变，也实现了平移、旋转等不变形，在鲁棒性方面有良好保持。

3 结 语

在消防体系中，要实现自动化系统的构建，特征点的提取是基本工作之一。总体来说，特征点的有效、快速确定，是摄像机自标定准确程度和工作效率的直接影响因素，因此必须给予充分关注，才能发现问题，不断改进。