钢-玄武岩纤维复合筋抗拉性能试验研究
孙胜江,赵 磊,2,梅葵花,李航宇,邢丽丽
(1.长安大学 公路学院, 陕西 西安 710064;2.陕西机勘工程检测咨询有限公司, 陕西 西安 710043)
0 引言
在传统建筑材料中,因钢筋混凝土优良的性能在现代土木工程中被广泛应用,但由于钢筋的耐腐蚀性差,较大程度地降低了结构整体的耐久性。而FRP材料具有高强、轻质及抗腐蚀性强等优点,其中抗腐蚀的特性可有效弥补钢筋易腐性的缺点。为了充分发挥钢筋和FPR各自的优势,可将两种材料复合制成耐腐蚀、高延性的新型复合材料。
在复合筋研究领域中,国外学者Nanni 等[1]较早提出利用杂交复合材料双线性的特点提高FRP增强混凝土结构延性。Harris等[2]通过对复合材料棒表面进行双向编织缠绕,使得界面韧性进一步增强。Ehsani等[3]通过将复合筋表面变为螺纹肋,使筋材与混凝土之间的黏结面积增大,进而达到抑制裂纹沿着黏结界面方向发展的目的。而国内在复合筋方面的研究起步相对较晚,但近年来其发展迅速。杨正光等[4]对玻璃纤维混杂筋的试验证明了可以通过结构设计提高FRP的延性。郑百林等[5]对玻璃纤维混杂筋进行了轴向拉伸破坏试验,并与其提出的理论曲线吻合较好。何振[6]、崔益华等[7]对多种纤维混杂筋进行了抗拉性能试验研究,结果表明混杂筋具体较高的弹性模量和很好的延展性。
玄武岩纤维增强复合材料(BFRP)具有耐腐蚀、耐疲劳、强度高、质量轻、绝缘性好等特点,相比于其他纤维增强材料,其延性相对较好,经济环保[8-10]。但单纯将BFRP筋应用于混凝土梁时,由于BFRP筋弹性模量相对较低,结构受到正常使用极限状态的限制,致使BFRP的材料强度无法充分发挥[11]。为此,吴刚等[12-14]首次提出将钢筋与BFRP两种材料复合,获得一种强度高、弹模高、成本低且耐腐蚀的新型结构材料:钢-玄武岩纤维复合筋(Steel Basalt Fiber Composite Bars,简称SBFCB),它的内芯为普通钢筋、外包覆盖层为纵向连续玄武岩纤维。罗云标等[15]研究了钢-连续碳纤维复合筋和钢-连续玄武岩纤维复合筋的生产制备工艺,并对其进行了单向拉伸和疲劳往复荷载拉伸试验,结合试验结果提出了在往复荷载下复合筋的应力-应变曲线关系[16]。肖同亮等[17]对不同纤维含量钢-玄武岩纤维复合筋进行拉伸和压缩试验,发现纤维含量对筋材强屈比有较大影响,并针对拉压不对称的特性,给出了建议的卸载模量退化系数。顾兴宇等[18]对高模量的钢丝与玄武岩纤维制作成的复合筋力学性能进行了研究,并从理论上对钢丝-玄武岩纤维复合筋受力机理进行了分析,根据分析结果得到复合筋的应力-应变关系曲线,发现该曲线具有双折线性特征。
尽管国内外对复合筋的受力特性开展了广泛的研究,但是对于SBFCB的力学性能研究很少,极其缺乏相应的试验数据与理论研究。研究SBFCB筋材本身的力学性能是将SBFCB应用于混凝土结构的基础,相比较单一的FRP筋和普通钢筋,SBFCB的受力状况、破坏形态以及抗拉强度的影响因素更为复杂。本研究进行SBFCB单向拉伸试验,并对SBFCB在单向加载下的应力-应变关系理论模型进行推导与评价。
1 试验方案
本次试验对3种不同玄武岩纤维-钢含量比的SBFCB进行拉伸试验,测定其初期弹性模量、二次刚度、屈服强度以及极限强度,并观察它们的破坏过程及特征。
1.1 试件规格
试验中玄武岩纤维复合筋的内芯为8 mm的螺纹钢筋,如图1所示。为考虑不同的玄武岩纤维-钢含量比对筋材力学性能的影响,使用3种不同的纤维用量试件(20束、30束、40束),相应的试件编号为B1,B2和B3,试件长度均为1.7 m,SBFCB的型号及组成材料如表1所示,组成材料的基本性能参数如表2所示。

图1 SBFCB构造图Fig.1 Structural diagram of SBFCB

表1 SBFCB试件型号Tab.1 The Type of SBFCB Specimen

表2 组成材料的基本性能Tab.2 Mechanical Properties of Component Materials
1.2 试验设备及方法
为保证拉伸试验的正常进行,试验之前必须在SBFCB两端作锚固处理。SBFCB是典型的各向异性材料,玄武岩纤维的横、纵向强度比小,无法采用传统的夹片式锚具,否则会因为外包玄武岩纤维横向强度较低导致其在锚固区提早破坏失效,故试验中采用专门设计的直筒黏结式锚具锚固SBFCB。试验之前先用除锈剂对锚具内部进行除锈处理,黏结介质采用环氧树脂胶。先对筋材一端的锚具灌胶,在灌胶过程中,通过锚具两端的定位板确保筋材处于锚具的中心线上,当锚具内部被环氧树脂胶灌满后,将锚具养护7 d,待环氧树脂完全固化后,再对筋材另一端的锚具灌胶,并将其置于相同的条件下进行养护,养护7 d后方可进行试验,最终锚固好的试件如图2所示。

图2 SBFCB试件Fig.2 SBFCB specimen
试验采用液压穿心式千斤顶进行加载,装置如图3所示。筋材的张拉力通过压力传感器来测定,筋材的拉伸应变采用YB-15数显手持式应变仪和在筋材的中间部位粘贴电阻式应变片两种方法来测量并相互校核,应变片黏贴在筋材凸起的肋处,粘贴前需要打磨平整。在筋材末端布置百分表用来测试筋材的滑移。所有的应变片以及百分表均连接到DH3817动静态应变测试系统上进行数据采集。

图3 试验装置Fig.3 Test setup
将筋材、压力传感器、千斤顶、反力架等安装完毕,一切准备工作就绪后开始加载。本次试验采用张拉力控制的加载方法,采用分级加载,但因千斤顶油压手动难以精确控制,故不是严格分级,加载速率约为0.5 kN/s,一直加载至外包玄武岩纤维破坏。
2 试件破坏过程及破坏形态
整个试验过程,以内芯钢筋屈服和外包纤维断裂为分界点,可分为3阶段:加载初期,复合筋处于弹性工作状态,此时由外包玄武岩纤维和内芯钢筋来共同承担所施加的荷载;随着荷载逐渐增大,当复合筋的应变约为0.002时,复合筋的内芯钢筋达到屈服,钢筋应力保持不变,由玄武岩纤维来承担新增的荷载,表现为筋材的应变增长减缓。随着所施加的荷载持续增大,可听到外包纤维由于断裂而发出刺耳响声;当达到极限荷载时,伴随着巨大的声响,SBFCB细丝状炸开破坏,如图4所示。随后承载力迅速下降至内芯钢筋屈服时荷载。由于试验装置的原因未能测试内芯钢筋断裂的过程。此外,试验之前将锚具进行端堵处理,防止筋材在破坏之前被拔出,试验完成后发现锚具孔口处没有明显变形和裂纹,表明此锚具对复合筋的锚固效果很好,如图5所示。试件破坏位置基本在筋材的中间区段,靠近锚具的部位几乎没有发生纤维破坏,同时也没有出现纤维与内芯钢筋剥离的现象。

图4 SBFCB破坏形态Fig.4 Failure Modes of SBFCB Specimens

图5 锚具端部状态Fig.5 The Status of Anchorage End
3 试验结果及分析
3.1 SBFCB力学性能理论分析
试验结果表明,复合筋外包纤维层与内芯钢筋在承受荷载作用的过程中黏结完好,变形一致,直至外包纤维破坏,因此可以运用复合法则求出钢-玄武岩纤维复合筋的受拉特性值,该法则假设外包纤维层与内芯钢筋在荷载作用下变形协调,同一截面处应变相等[15]。
采用理想弹塑性模型模拟内芯钢筋应力-应变曲线,即假设内芯钢筋为完全弹塑性材料;采用完全线弹性模型模拟玄武岩纤维的应力-应变曲线,即玄武岩纤维在整个过程中为完全弹性。两种材料复合后对理论应力-应变曲线进行分析:复合筋应变小于0.002时,应力-应变曲线为直线;随着荷载的增加,当复合筋应变值为0.002时,内芯钢筋开始屈服;此后,增加的荷载全部由外包玄武岩纤维来承担,表现为钢筋应力增长速度变缓。此时应力-应变曲线依然成线性关系,但斜率比钢筋屈服之前小,外包纤维应变按照此时的速率逐渐增加,直至极限应变而破坏。外包纤维破坏后,荷载突然降至内芯钢筋屈服时的量值,直至内芯钢筋断裂。在加载前两个阶段,应力-应变曲线呈现出双折线特性。
图6为SBFCB理论应力-应变关系示意图,从开始加载到钢筋屈服为第Ⅰ阶段,这一阶段复合筋的弹性模量记为EⅠ,拉应力记为σⅠ,根据材料复合法则,其表达式为:
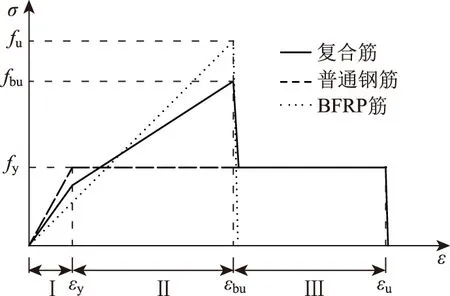
图6 SBFCB理论应力-应变关系示意图Fig.6 Theoretical Stress-strain Curve of SBFCB
EⅠ=(EsAs+EbAb)/A, 0≤ε≤εy,
(1)
σⅠ=εEⅠ=ε(EsAs+EbAb)/A, 0≤ε≤εy,
(2)
式中,Es,As,εy为钢筋的弹性模量、截面积、屈服应变,εy取0.002;Eb,Ab为外包纤维的弹性模量、截面积;ε为复合筋的应变;A为复合筋的总面积,A=As+Ab。
自钢筋屈服到外包玄武岩纤维断裂失效,记为第Ⅱ阶段,这一阶段的弹性模量记为EⅡ,拉应力记为σⅡ:
EⅡ=EbAb/Aεy<ε<εbu,
(3)
σⅡ=εyEⅠ+(ε-εy)EⅡ=(fyAs+εEbAb)/A,
εy<ε<εbu,
(4)
式中,fy为钢筋的屈服强度;εbu为外包纤维的断裂应变。
自外包纤维断裂至内芯钢筋断裂,记为第Ⅲ阶段,这一阶段的弹性模量记为EⅢ,拉应力记为σⅢ:
EⅢ=0,εbu<ε<εu,
(5)
σⅢ=fy,εbu<ε<εu,
(6)
式中εu为钢筋的断裂应变。
3.2 试验结果验证
根据材料复合法则推导的公式(1)~(6),并结合表1、表2中材料的物理力学性能,可以计算出3种规格SBFCB的弹性模量、屈服强度、极限强度等参数的理论值。利用试验数据, 计算出参数的试验值,其中屈服强度和极限强度分别由屈服荷载和极限荷载除以实测截面面积所得,弹性模量的试验值是根据试验结果采用线性回归所得,试验结果及其与理论值的比较如表3所示。

表3 试验结果及与理论值比较Tab.3 Test Results and Comparison with Theoretical Values
由加载值计算筋材应力,不同型号SBFCB试件的应力-应变曲线如图7所示。
由表3和图7可见, SBFCB的应力-应变曲线均呈明显的双折线形;钢筋屈服前,复合筋的应力-应变曲线与理论值非常接近。钢筋屈服后,复合筋表现出明显的二次刚度,因玄武岩纤维弹性模量小于钢筋的弹性模量,复合筋的二次刚度要小于钢筋屈服前的刚度。SBFCB的实测屈服应变和屈服强度与理论计算值接近,说明内芯钢筋与外包玄武岩纤维在钢筋屈服之前有效黏结,两者共同受力。SBFCB的实测极限应变和极限强度略小于理论计算值,这是因为内芯钢筋屈服后无法保证所有玄武岩纤维与内芯钢筋变形同步,少量玄武岩纤维先期达到极限应变和极限强度。SBFCB中玄武岩纤维-钢含量比越大,其初始弹性模量越小,但内芯钢筋屈服后复合筋的二次刚度越大,与理论计算结果相符。SBFCB的破坏属于延性破坏,随着荷载的增加,经历了明显的应变增大过程,其延性介于普通钢筋和玄武岩纤维之间。
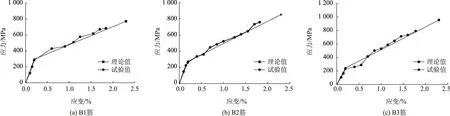
图7 SBFCB试件的应力-应变曲线Fig.7 Stress-strain Curve of SBFCB
4 结论
本研究对3种不同玄武岩纤维-钢含量比的SBFCB进行拉伸试验,并依据材料的复合法则,推导出SBFCB单向拉伸的应力-应变曲线模型,将试验值与理论值进行对比,得出以下结论:
(1)在拉伸试验过程中,随着荷载的增大,内芯钢筋先发生屈服,后由外包的玄武岩纤维承受更大的荷载,当达到外包纤维极限强度时,复合筋外包纤维突然炸裂破坏,属于延性破坏且有明显破坏预兆。
(2)钢筋屈服前,复合筋弹性模量高于纯玄武岩纤维筋,应力-应变关系为线性;当内芯钢筋屈服以后,复合筋能继续承受更大的荷载,表现出了明显的“屈服后刚度”。试验中所得到的应力-应变关系与理论值相符,均为双折线本构模型。
(3)SBFCB的实测屈服应变和屈服强度与理论计算值接近,说明内芯钢筋与外包玄武岩纤维在钢筋屈服之前有效黏结,两者共同受力。
(4)复合筋中玄武岩纤维-钢含量比越大,其初始弹性模量越小,但它的二次刚度以及极限强度更大,与理论计算值相一致。
本研究通过对SBFCB进行单向拉伸试验,得出SBFCB的破坏形态和破坏性质,证实了纤维复合筋的优越性,并根据试验数据对比理论结果,验证了双折线模型的正确性,为后续SBFCB的工程应用打下基础。本研究提及了玄武岩纤维-钢含量比对测试参数的影响,下一步还需要深入讨论其适当的取值范围。
——钢绞线的断束断丝的防治及发生时采取的措施

