生态袋包裹粉质黏土三轴试验研究
蒋希雁 许梦然* 陈宇宏 冯 峰 杨尚青
(1.河北建筑工程学院 土木工程学院,河北 张家口 075031;2.河北省土木工程诊断、改造与抗灾重点实验室,河北 张家口 075031;3.河北省寒冷地区交通基础设施工程技术创新中心,河北 张家口 075031)
0 引 言
生态护坡是在坡体种植植物与已有的工程坡体形成综合系统的护坡技术,它利用植被对坡面进行保护同时也增加了绿化效果[1-3].生态袋护坡技术是一种常见的生态护坡技术,其主要由生态袋、联结扣、土工格栅、编织土工布等几种元素构成.生态袋防护工程是与绿化工程同步进行,可以有效的缩减施工工期,同时在生态袋护坡施工过程中不使用水泥、钢筋等传统建材,不产生建筑垃圾,有效的降低了对环境的污染[4-6].钦志强[7]等通过介绍桐乡市无量桥港的生态堤岸试验工程,说明了柔性生态袋在河道生态建设中的重大作用;李润成[8]通过描述生态袋护岸工程在汾河流域生态修复中的成功案例,总结出生态袋护岸技术适应新时代绿色发展的需求,且造价低、施工技术简单,具有广泛的应用前景;刘斯宏等[9]介绍土工袋加固地基的原理、基本特性,以及土工袋在实际工程中的使用,说明了土工袋加固地基的过程中利用了土工袋在外部荷载下袋子周长变长而产生的张力,同时袋子张力引起一个附加粘聚力;白福青等[10]在此基础上对土工袋的加固原理进行分析,推导出土工袋二维和三维强度公式,通过试验研究发现,三维土工袋强度模型比二维模型更加符合实际情况;夏家南[11]等进行了土工布包裹对粗粒料三轴试验的影响研究,得到了粗粒料三轴试样包裹土工布后,试样的强度得到提高,内摩擦角基本不变,而粘聚力得到明显的提高;程飞龙[12]等对生态袋破坏机理进行分析,并给出了对于单轴压缩试验,生态袋内部土体处于极限破坏时的公式,但未进行生态袋处于三维应力状态时的研究分析.
本文以三维应力状态分析生态袋加固原理,基于Mohr-Coulomb强度破坏准则[13],推导出生态袋张力所产生的附加粘聚力的计算公式.通过在三轴试样四周表面包裹生态袋的方法来模拟粉质黏土在生态袋包裹下的环境,对包裹生态袋和未包裹生态袋的粉质黏土试验进行常规三轴不固结不排水试验,分析研究生态袋包裹对试样的应力-应变关系、强度特征的影响,并对比试验值是否与理论公式计算值相吻合.
1 生态袋强度提高原理
1.1 生态袋破坏机理
将土石材料装入具有一定规格与材料特性,一端开口的编织袋中形成的生态袋,在外力作用下,袋子被压扁,袋内填土向两侧移动,引起袋子周长的伸长,在袋子中产生了一个张力,袋子张力反过来又约束生态袋内部的土体,使得袋内土颗粒间的作用力增大,从而增大袋内土体的抗剪强度.
生态袋是一种具有蠕变性质的土工织物材料,在袋内土体共同受力的过程中,最初沿着受拉方向生态袋的应变增量与袋内土体应变增量相等.由于生态袋与土体抗拉性质的差异,当袋内土体侧向应变超过其极限应变时,土体被拉坏,将不能继续承受拉应力全部的侧向土压力将由生态袋承受.生态袋的抗拉力来源于生态袋与土体之间的摩擦力.
1.2 公式推导
为方便分析,做如下假定:
(1)生态袋压实后,侧向一般呈外凸的弧形,为了方便计算,假定生态袋受力后外观为三维的六面体,长、宽、高分别为L、B、H.
(2)作用在生态袋六面体上的外力用主应力表示,分别为大主应力σ1m,中主应力σ2m,小主应力σ3m.如图1所示:大主应力方向σ1m与生态袋z轴平行;中主应力方向σ2m与生态袋y轴平行;小主应力方向σ3m与生态袋x轴平行;

图1 三维应力状态下生态袋受力分析图
(3)生态袋强度公式的推导是基于Mohr-Coulomb强度破坏准则.主应力σ2=σ3的轴对称情况,未考虑到中主应力σ2的影响,忽略了该方向由袋子张力所产生的附加应力.在实际护坡工程中,临空面附近的生态袋,其σ2与σ3并不相等.
生态袋在外力σ1m,σ2m,σ3m作用下,袋子周长伸长,从而产生一个张力T,根据图1各中截面的受力平衡条件,可得由于张力T作用,在生态袋内部土体产生的附加应力:
(1)
式中:Δσ1、Δσ2、Δσ3分别为在H、L、B方向产生的附加应力;T为生态袋材料的张力,kN/m;L、B、H分别为生态袋六面体的宽、长、高,m.
从袋内土体中取出一微单元体,作用在该单元体上的总应力为外部应力(Δσ1m,Δσ2m,Δσ3m)与张力T引起的附加应力(σ1,σ2,σ3)之和,如图2所示:
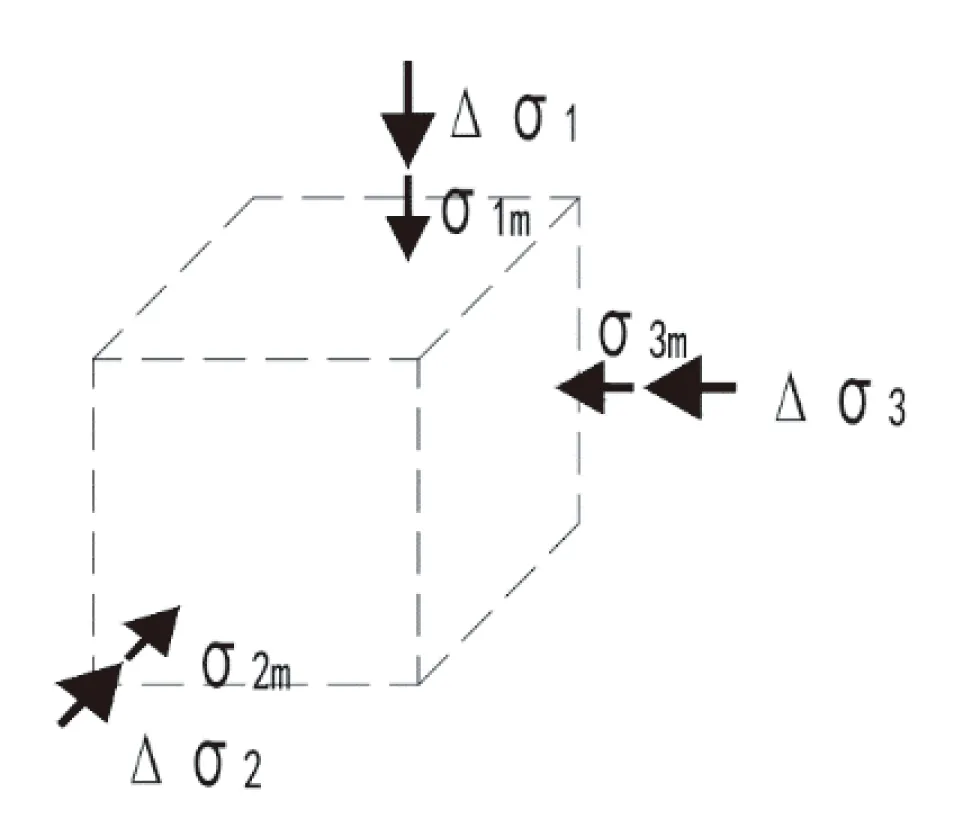
图2 袋内土单元上的应力
(2)
将式(1)代入式(2)得:
(3)
式中:σ1f,σ2f,σ3f分别为袋内土体大、中、小主应力,kPa;σ1m,σ2m,σ3m作用在生态袋上的外力,分别用大、中、小主应力表示,kPa;T为生态袋材料的张力,kN/m;L、B、H分别为生态袋六面体的宽、长、高,m.
当袋内土体处于极限平衡状态时,根据Mohr-Coulomb强度破坏准则,如图3中虚线所示:
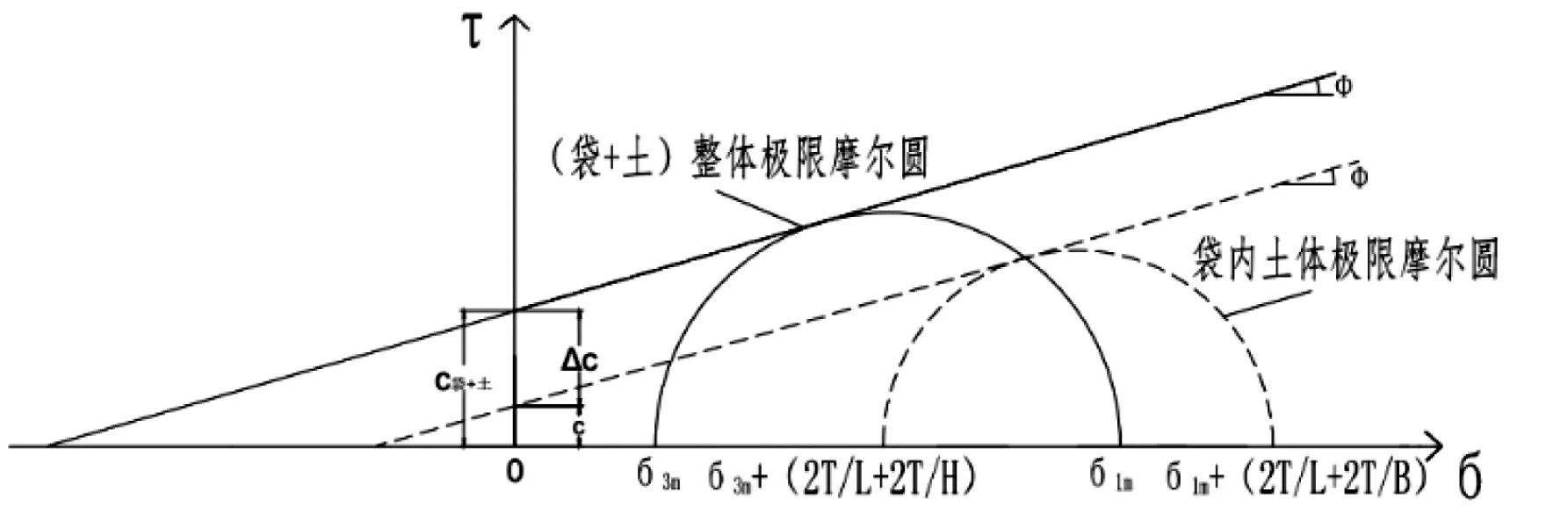
图3 极限平衡状态时的摩尔圆
可得袋内土体大、小主应力关系为:
(4)
式中:c为袋内土体的粘聚力,kPa;φ为袋内土体的内摩擦角,(°)
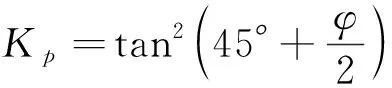

(5)
式中:Δc为由袋子张力产生的附加粘聚力,kPa;
则得:
(6)
假定土体装入生态袋后,其内摩擦角φ保持不变,此时,可将生态袋连同袋内土体作为一种复合材料,其对应的极限摩尔圆如图3中的实线所示.
由式(5),可知,生态袋整体的粘聚力为袋内土体本身的粘聚力与袋子张力所产生的附加粘聚力Δc之和,即:
(7)
由式(7)可知,生态袋的作用在于增加了一个附加粘聚力,而附加粘聚力Δc的大小与土体摩擦强度、袋体强度以及袋体尺寸有关.
1.3 附加粘聚力影响因素分析
(2)附加粘聚力与生态袋张力密切相关,生态袋张力T是在外力作用下产生的,当有外力作用时,其张力为零,生态袋不起作用;外力越大,张力T也越大,极限值为袋子的破坏强度,产生的附加粘聚力也越大,生态袋的强度越高.因此,生态袋强度提高的原动力是外力,蕴含着一个“借力打力”的道理.
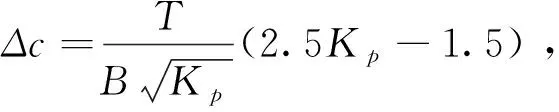
2 试验设计
2.1 试验仪器与材料
试验采用如图4所示的南京土壤仪器厂所生产的全自动流变三轴仪.三轴试样的直径为61.8 mm,截面积为30 cm2,试样的高度为125 mm.

图4 全自动流变三轴仪 图5 生态袋
本试验选用如图5所示仪征康顺土工材料有限公司所生产的生态袋,通过条带拉伸试验测定了生态袋在无侧限条件下径向和纬向的拉伸强度和伸长率,试验拉伸速率25 mm/min,其他相关性能参数见表1.

表1 生态袋基本性能参数
该实验用土为粉质黏土,其物理性质指标如表2

表2 试样土的物理性质指标
2.2 试验方法
试验土样按照《土工试验方法标准》(GB/T 50123-2019)[14]扰动样的制备程序对试样进行处理,试样用土采用最优含水率12%进行配置,按照压实度为0.85,分5层进行击实,各层接触面用小刀刨毛,每层土的质量相等,制成为直径为61.8 mm,高125 mm的圆柱体,如图6所示,将生态袋包裹在裸土试样四周并缝制,完成缝制后的试样因外部包裹生态袋,难以用常规承膜筒将橡皮膜套在试样外部,特制一个比常规承膜筒内径大4 mm的承膜筒,特制承膜筒如图7所示.

图6 包裹生态袋 图7 特制承膜筒
将制作的试样进行不固结不排水试验,模拟路堤边坡情况下,围压取50 kPa、100 kPa、150 kPa和200 kPa,相同条件下每个围压等级进行3个平行试验,剪切速率取1 mm/min,未包裹和包裹生态袋试样剪切进行至轴向应变为20%时终止试验.
3 试验结果分析
3.1 主应力差(σ1-σ3)与轴向应变(ε1)的关系
本试验共计进行2组试验,每组试验分为3个平行试验,共计24个试样.未包裹和包裹生态袋试验结果选取试样轴向应变的数据进行分析研究.图8~图10给出了未包裹与包裹生态袋试样在剪切过程的应力-应变关系曲线.由图可知:
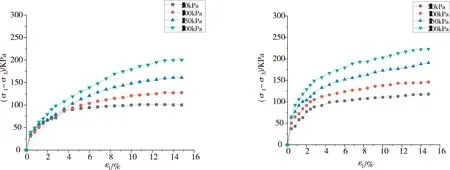
图8 未包裹生态袋试样应力-应变曲线 图9 包裹生态袋试样应力-应变曲线

图10 不同围压下有无生态袋试样应力-应变曲线
(1)随着轴向应变ε1的增加,主应力差(σ1-σ3)的值在不断增加,且无应力峰值,故包裹生态袋试样和未包裹生态袋试样的应力-应变曲线均呈现应变硬化现象.
(2)当应变较小(<3%)时,包裹生态袋试样和未包裹生态袋试样的应力-应变关系曲线很接近,生态袋作用不明显,但随着轴向应变的增大,包裹生态袋与未包裹生态袋试样的应力应变关系曲线逐渐加大且最终趋向于一定值,说明包裹生态袋的作用当轴向应变较大时才比较明显.
(3)当应变达到一定值后,在相同应变条件下,包裹生态袋试样的主应力差较未包裹生态袋试验的主应力差有显著的提高,或者在相同围压下,包裹生态袋试样的应力应变曲线位于未包裹生态袋试样曲线的上方,这说明包裹生态袋提高了试样强度.
3.2 抗剪强度指标
由于未包裹和包裹生态袋试样的应力应变曲线表现出硬化特点,因此将未包裹和包裹生态袋试样轴向应变15%对应的应力值作为其强度,在τ-σ应力平面图上绘制不同围压下(50 kPa、100 kPa、150 kPa、200 kPa)的摩尔应力圆和相应的应力圆包线如图11所示,可得未包裹和包裹生态袋试样的抗剪强度指标c、φ值,见表3.
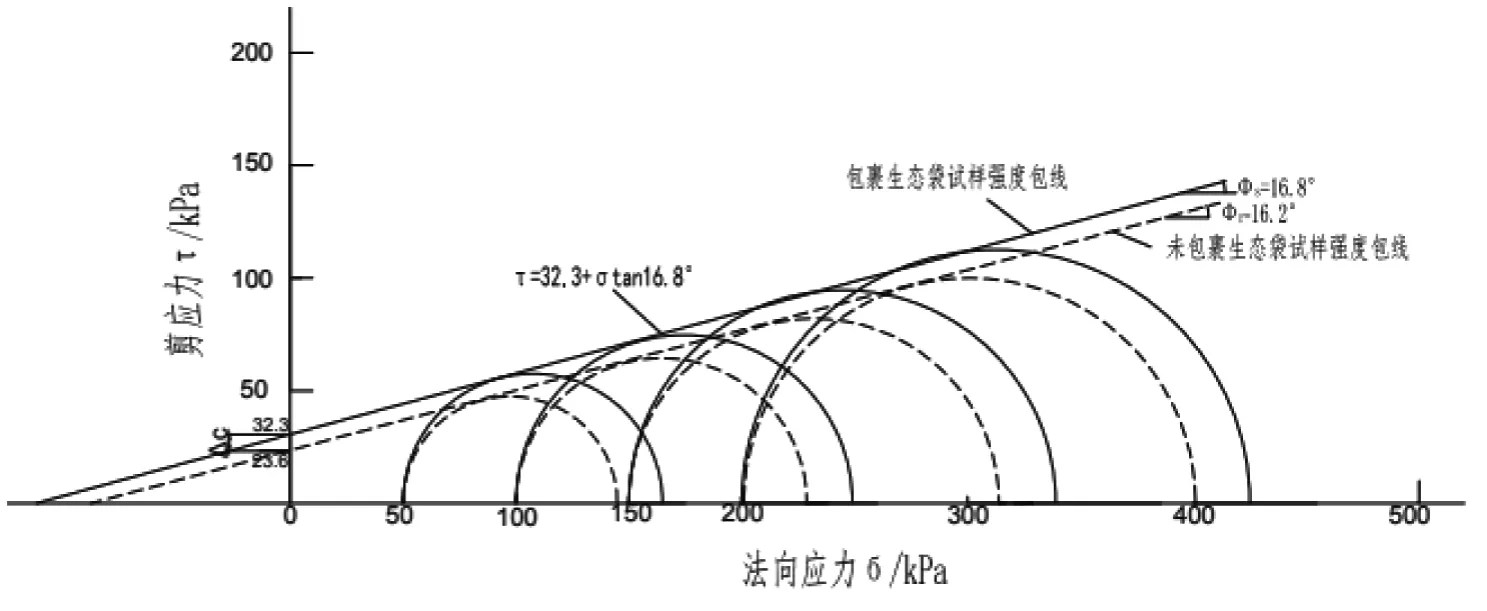
图11 包裹与未包裹生态袋试样的强度包线
为了评价生态袋包裹对粘聚力和内摩擦角的影响,设cs为包裹生态袋土的粘聚力,cr为未包裹生态袋土的粘聚力;φs为包裹生态袋土的内摩擦角,φr为未包裹生态袋土的内摩擦角;则粘聚力增长率εc=(cs-cr)/cr和内摩擦角相对误差εφ=(φs-φr)/φr变化值如表3所示.

表3 有无生态袋试样的抗剪强度指标对比
本次试验结果表明:
(1)包裹生态袋试样的内摩擦角与未包裹生态袋的基本相同,相对误差为3.7%.
(2)与未包裹生态袋试样相比,包裹生态袋试样的粘聚力有较明显的增长,增长率为36.9%.
综上所述,包裹生态袋与未包裹生态袋试样相比,在不同围压下试样的抗剪强度都有所提高,其原因在于,在试样被剪切的过程中,试样会发生变形,包裹在试样表面的生态袋也因此会被拉伸,生态袋会产生一个张力T,生态袋所产生的张力会反过来约束袋内的土体,从而使得袋内土体更不容易被剪坏.
3.3 理论公式与试验值对比
为了验证上述理论公式是否与实际相符合,故将三轴试验测得指标与数据代入理论公式.三轴试验试样为圆柱体,B=L,试样的直径为0.0618 m,高度为0.125 m.T为生态袋所产生的张力,其值最大不能超过径向/纬向拉伸强度较小值,在计算过程中,取径向拉伸强度1.37 kN/m(径向拉伸强度1.37 kN/m<纬向拉伸强度2.29 kN/m),但是在试样剪切过程中,生态袋未出现破损和拉坏现象,故对张力T乘以一个小于1的折减系数,折减系数取0.8.假定包裹生态袋后,袋内土体的内摩擦角未发生改变,取内摩擦角φ=16°.
根据上述三轴试验实际所得c袋+土(32.3 kPa)与理论公式所计算c袋+土(32.04 kPa)基本相吻合.该公式可以预测计算出生态袋附加粘聚力,为生态袋设计提供重要参考与依据.
4 结 论
(1)研究基于Mohr-Coulomb强度破坏准则推导得出了三维应力状态下生态袋强度公式,反映生态袋加固机理为生态袋张力提供了附加粘聚力,但该模型忽略了中主应力的影响,也忽略了该方向由袋子张力所产生的附加应力.
(2)根据附加粘聚力影响因素分析,可以通过调整生态袋尺寸大小、改换袋内土体材料和提高袋体强度的方式来使附加粘聚力达到一个较大值.
(3)三轴试验结果显示,生态袋包裹试样比未包裹生态袋试样的强度更高;包裹生态袋与未包裹生态袋试样的应力-应变曲线变化趋势相同,都呈硬化现象;生态袋的包裹作用只有在当应变较大时才发挥作用才明显.
(4)生态袋包裹试样与未包裹生态袋试样的内摩擦角相差甚小(可忽略不计),而粘聚力则有相应的提高,约是未包裹生态袋试样的1.37倍,说明生态袋作用在于增加了一个附加粘聚力.
(5)理论公式求得的生态袋附加粘聚力与试验测得值基本相吻合,可以通过理论公式对生态袋强度进行预测,为生态袋设计提供重要参考.

