层状场地中粘弹性人工边界古城墙地震反应分析

唐晓荣 周占学,2* 于 爽 李 杨 袁晓聪

(1.河北建筑工程学院，河北 张家口 075000；2.河北省土木工程诊断、改造与抗灾重点实验室)

0 引 言

古城墙是我国历史上建筑文化的传承，是古代劳动人民的智慧的象征，是历史传承的使者，对其抗震研究有助于古建筑的保护与发展，高衡[1]等人对西安城墙砖进行分析，研究其组成成分及力学性能，得出现存古城砖机械性能一般，高大峰[2]等人对西安城墙进行实验研究，分析结构下地震激励下的动力反应和动力特征.刘琨[3-4]等人对高昌故城内城墙墙体进行现场脉动实验，分析城墙不同部位速度放大效应，研究动力响应特征，为城墙抗震加固提供参考依据.

以张家口大境门古城墙为参考，利用ABAQUS有限元软件建立古城墙模型和土-古城墙模型，采用刘晶波教授等人粘弹性人工边界理论[5-7]添加人工边界，文中进行模态分析，得到两个模型的自振频率和周期，再选取El-Centro、Taft、天津波三种地震波进行地震分析，得到两个模型的位移时程曲线和加速度位移时程曲线.

1 有限元模型建立

1.1 模型概况

大境门的古城墙是用夯土筑建而成，土层比较均匀、紧密，处于坚硬和应诉状态，土体夯筑后在夯土的两侧包上数层的青砖，城墙砖尺寸大于普通的烧结砖，城墙砖之间的接缝采用白灰浆砌筑，白灰浆在古代是将糯米加入到石灰砂浆中搅拌而成，城墙地基多采用条石地基，基础埋深1.5米，模型全长100米，高度10米，城墙下部宽度为6.4米，上部宽为5米，中间门洞为拱形门，整体宽度为5米，高度为6.5米，城墙下部土层取长度100，土层厚为40米.有限元模型如图1所示.

图1 有限元模型

1.2 模型材料及参数

大境门古城墙结构采用的是内部夯土筑建外部包砖的形式，属于砖土结合，通过对城墙土的实验研究8]得到古城墙夯土材料参数如下表所示：

(a)古城墙模型 (b)土-古城墙模型

表2 城墙砖砌体材料参数表

在进行土—古城墙相互作用分析时，截取城墙下一定范围的土层，在不同土层施加相应的人工边界来替代古城墙结构下部无限土域，由于大境门城墙附近的地质资料不够充分，现有条件不允许进行钻孔勘察，所以采用天保·蔚州城岩土工程勘察的蔚县县城的地质勘察资料，其土层参数见下表：

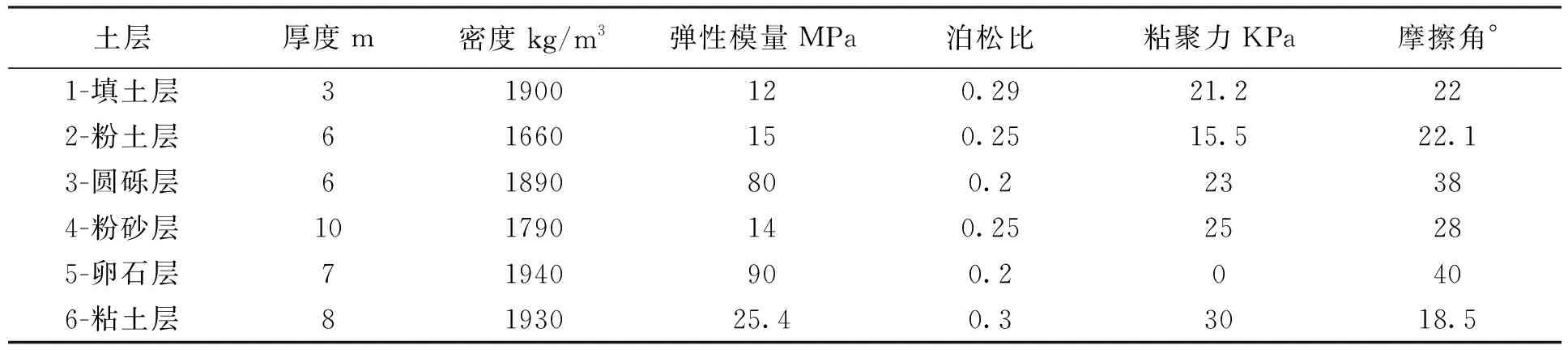
表3 层状土层参数

1.3 本构关系

城墙结构采用外部包砖、内部夯土的形式，有效提高城墙防水能力，防止风雨侵蚀，同时提高城墙的坚固程度.由于城墙外包砖的极限强度和弹性模量远大于内部夯土，考虑包砖与夯土相互作用，将包砖砌体模型简化成各向同性且材料均匀的线弹性模型，城墙夯土采用Mohr-Coulomb模型.

由于城墙下的土体材料、参数不同，对应采用本构关系也不同，考虑到土体的动力非线性，文中采用了等效线性模型，该模型通过迭代来近似反应土体的非弹性和非线性，是土层地震动反应分析的主流方法，在水平成层场地应用广泛.

利用ABAQUS提供的用户子程序作为二次开发平台，在输入文件中，使用关键词定义用户材料，在用户材料子程序中可以实现定义材料的本构关系，文中利用其基本原理编制Fortran程序，在ABAQUS有限元软件中调用子程序，作为土体的本构关系.

1.4 人工边界的条件及选择

人工边界是对人们在处理无限连续介质问题时人为引用的虚拟边界，目的在于简化问题，便于计算，现实情况下，建筑结构并不是处在封闭的空间中，它是半无限的状态之下，在有关有限元模拟分析中，有限元软件只能将模型定在一定范围之内，模型所包含的范围场地称之为自由场，从而引入了人工边界的研究，为了确保分析结果的精确性和严谨性，国内外众多学者进行了大量的研究与分析，并取得了许多有价值的成果，本文采用的是刘晶波教授粘弹性人工边界理论.其中弹簧元件的弹性系数KB和阻尼系数CB计算公式如下：

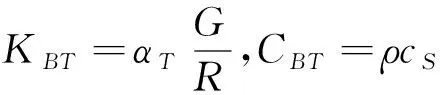
其中，G为介质的剪切模量；ρ为介质的质量密度；R为散射源到人工边界节点的距离，cs是介质中的S波波速，cp是介质中的p波波速，参数α为人工边界参数.取值参考下表4

表4 粘弹性人工边界αT、αN取值范围

2 结构动力特性分析

模态分析是一种研究结构动力学特性的方法，模态分析又称为自由振动分析，模态分析是一种处理过程，是根据结构的固有特性，包括频率、阻尼和模态振型，这些动力学属性去描述结构的过程，通过模态分析可以确定结构的固有频率、周期及振型.是结构进行动力分析首要考虑的问题.

模态分析的目的在于求系统的固有频率和振型.在有限元处理主要步骤大概有：建立模型、施加边界条件、求解设置、后处理等，模态分析是线性分析，忽略非线性.

对于模态分析，动力平衡方程：

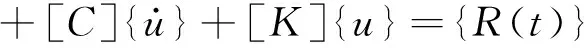
这里[M]是结构总质量矩阵；[C]是阻尼矩阵；[K]是结构总刚度矩阵；{u}是结构位移向量；{R(t)}是强迫力矩阵

2.1 结构模态分析

下面对古城墙模型、土-古城墙模型分别进行的模态分析，确定各个模型的动力特性，并提取前十阶模态振型，其固有频率及固有周期如图所示：

(1)古城墙自振频率.

(2)古城墙前六阶振型.

第一阶振型

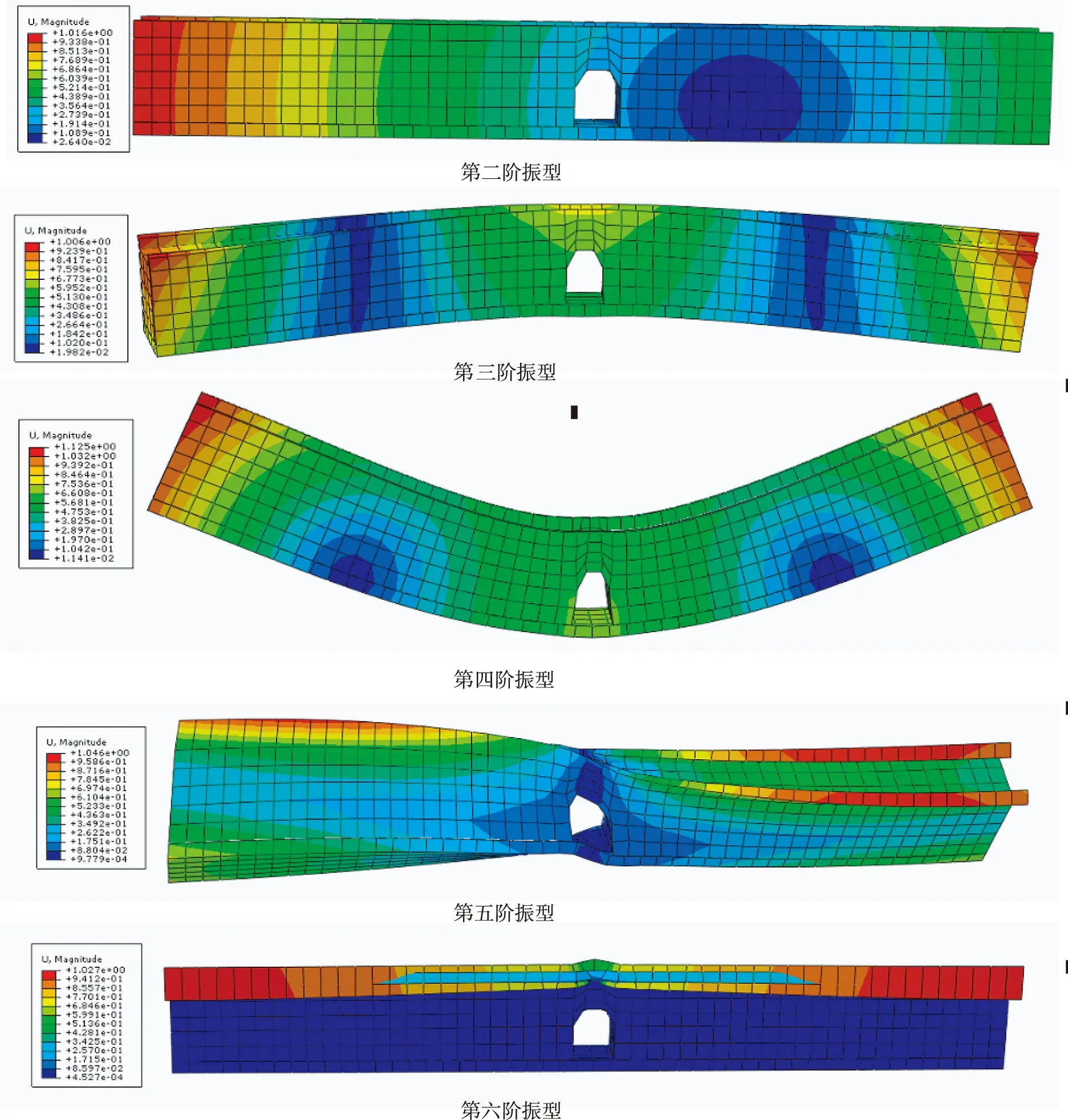
图2 古城墙结构模型前六阶振型

由表5及上列各图可得，大境门古城墙结构的基本频率为0.945，基本周期为1.058，结构的第一、二、三阶次自振频率数值相近.前十阶振型介于0.945～5.355之间，古城墙结构布置较为规整，一、二阶振型主要以沿着X方向平动为主，从第三阶振型开始出现了明显的扭转特性.各阶模态变形最大值均以城墙顶部变形为主，可知城墙顶部在结构固定频率下容易发生变形.

表5 古城墙模型自振频率

(3)土-古城墙自振频率.

(4)土-古城墙前六阶振型.

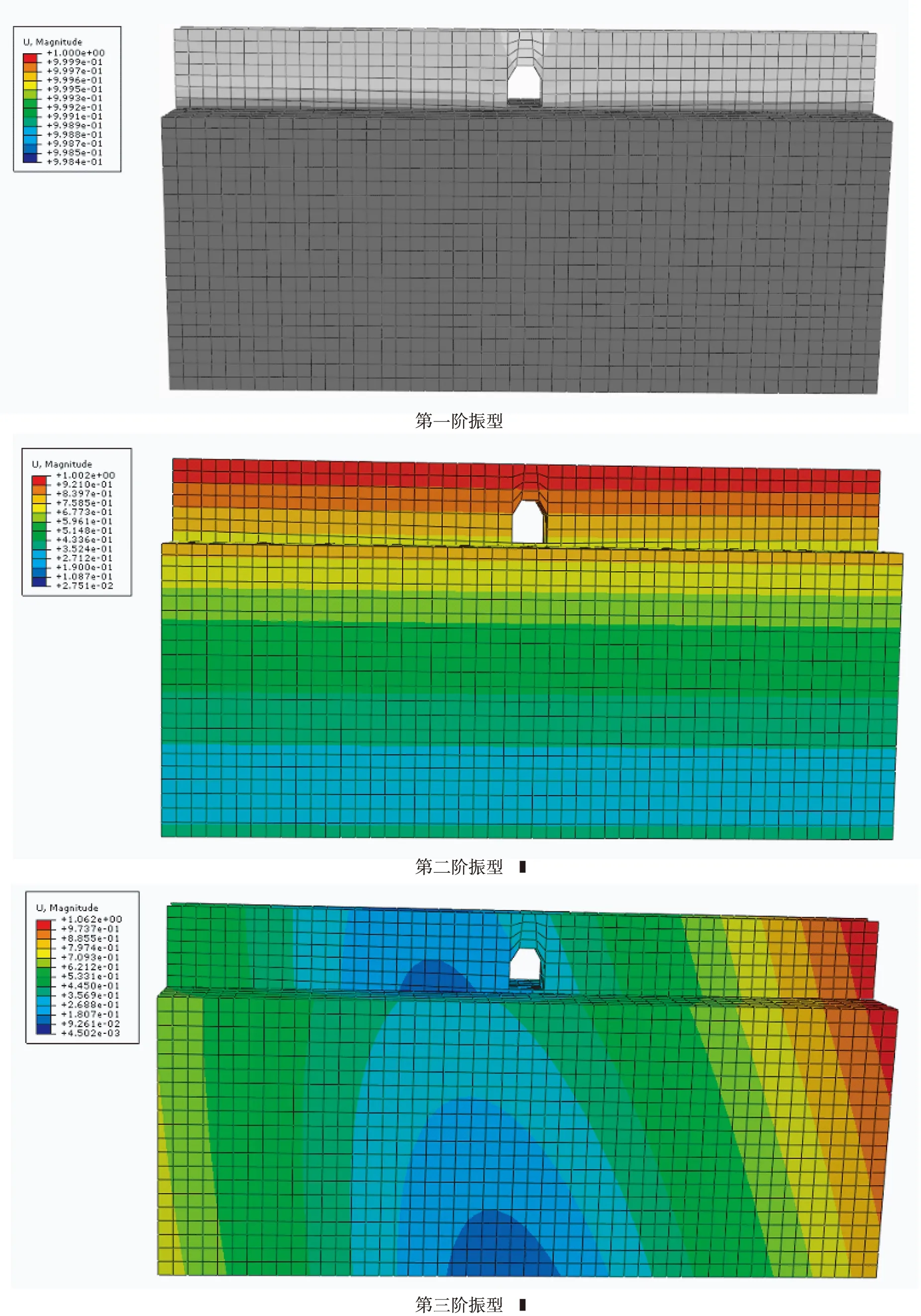
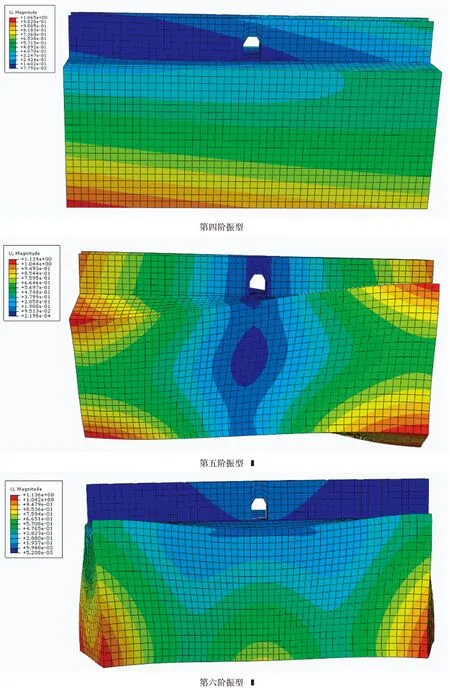
图3 土-古城墙结构模型前六阶振型

由表6及上列各图可得，土-古城墙结构的基本频率为0.522，基本周期为1.916，前十阶振型介于0.522～1.143之间，第一、二、三阶自振频率数值相近，主要以古城墙模型振动为主，从第四阶次开始振动主要是由土层带动了上部结构共同振动.

表6 土-城墙结构模型自振频率

2.2 模型模态结果分析对比

将城墙结构模型与土-城墙结构模型的自振频率绘制成如下图所示，对比如下：

通过分析图4可以得出：与古城墙模型相比，土—古城墙模型自振频率相对于古城墙模型较小，第一、二、三阶振型主要表现为古城墙结构模型的振动，第四阶开始振型基本上是下部土层和上部古城墙结构共同参与振动，随着阶次的增加，土-古城墙结构自振频率的增加幅度相比较而言更为平缓，考虑到土与结构共同作用时对结构频率影响较大，即土层结构存在改变了古城墙结构的自振特性，土-古城墙模型的频率较小而周期较长，这是由于土层的柔性而使得结构的自振周期延长.

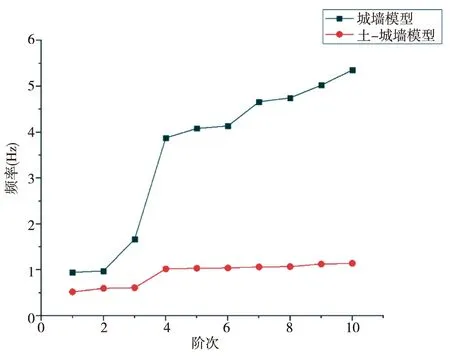
图4 两种结构频率变化对比曲线

3 地震分析

根据《建筑抗震设计规范》GB50011-2010中可以得到，张家口市区的抗震设防烈度为7度，设计基本加速度为0.15 g，设计地震分组为二组，大境门古城墙所在场地为二类场地，本文选取地震波El-Centro波、Taft波及天津波，通过调幅，对模型输入三种地震波，进行时程分析，输入节点的加速度和位移时程数据.

3.1 El-Centro波激励下结构反应

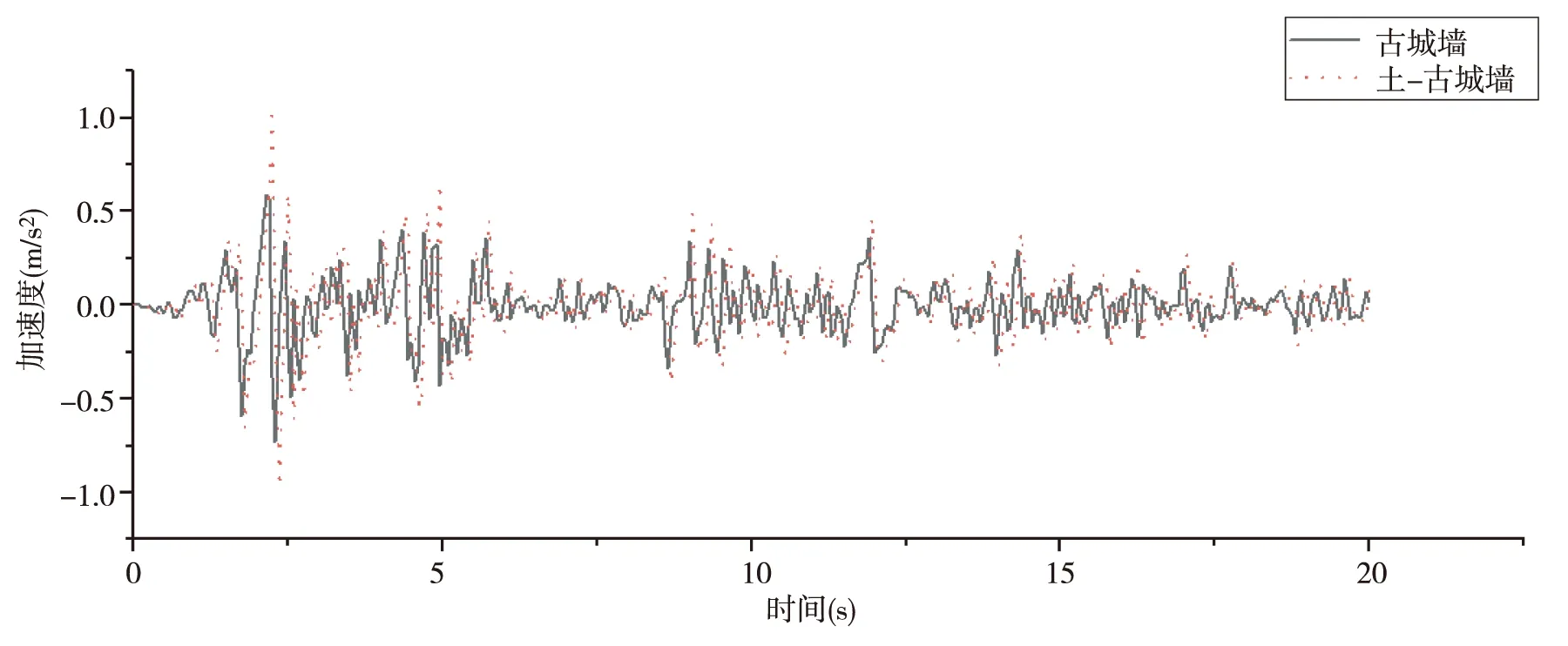
图6 El-Centro波激励下顶部节点加速度对比

由图5、6可以看出，输入修正后的时间20 s的El-Centro地震波，上部结构古城墙顶部最大位移为10 mm，其发生的时刻为2.65 s，最大加速度值为0.73 m/s2，其发生的时刻为2.3 s，土-古城墙整体结构城墙顶部最大位移为12 mm，其发生的时刻为2.75 s，最大加速度值为1.02 m/s2，其发生的时刻为2.25 s.

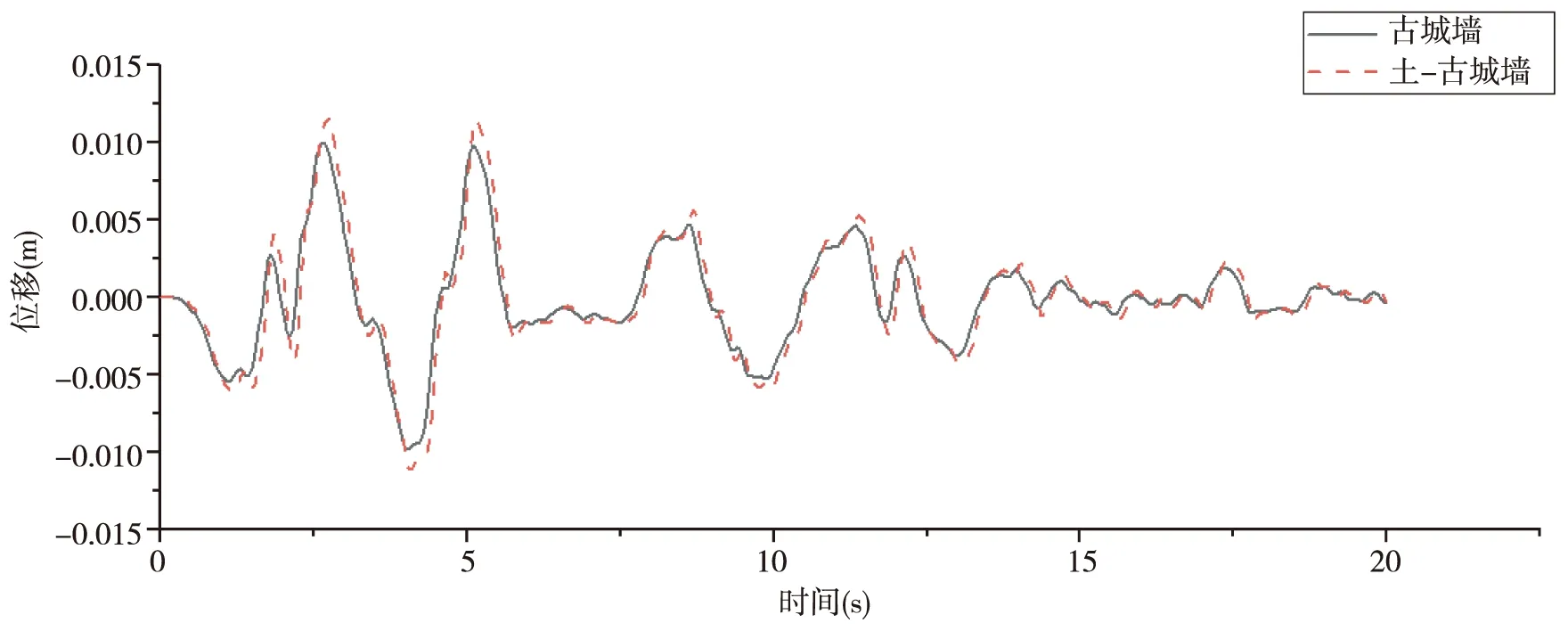
图5 El-Centro波激励下顶部节点位移对比

3.2 Taft波激励下结构反应

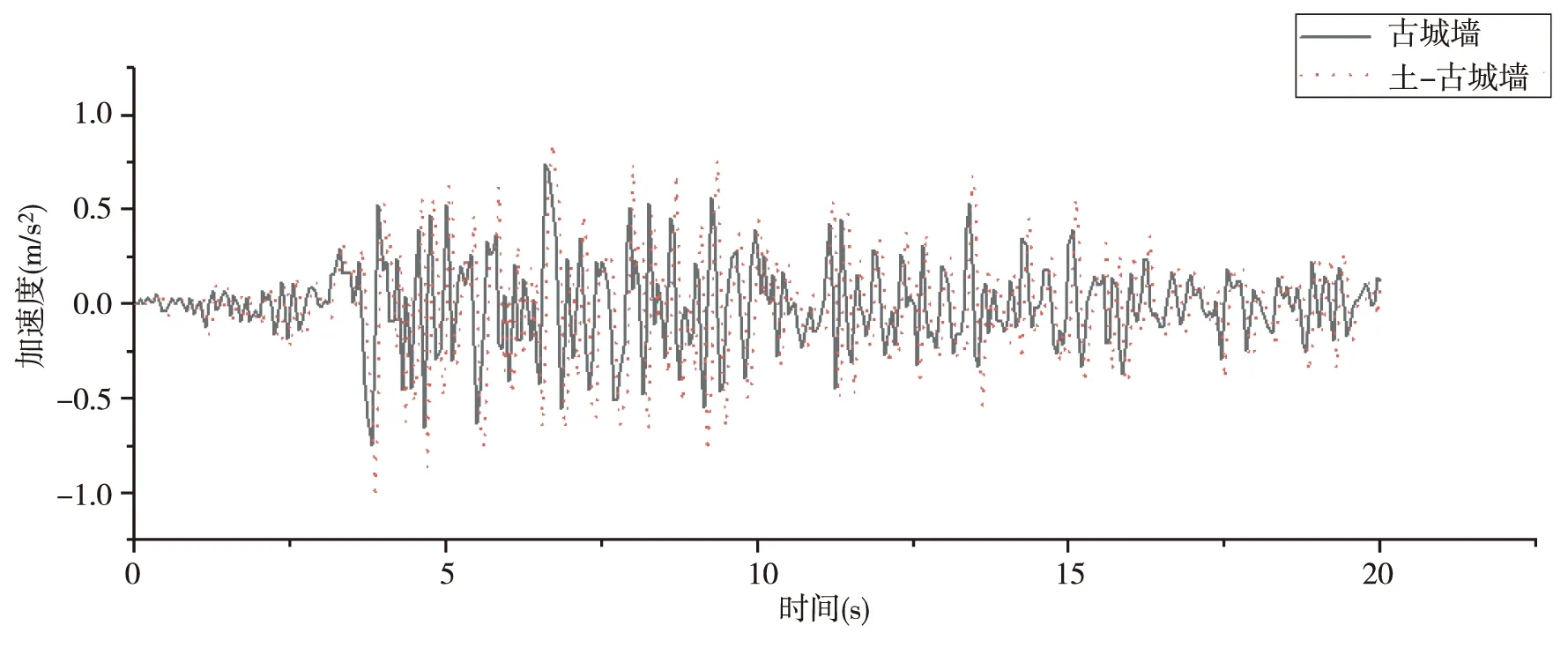
图8 Taft波激励下顶部节点加速度对比

由图7、8可以看出，输入修正后的时间20 s的Taft地震波，上部结构古城墙顶部最大位移为14 mm，其发生的时刻为6.65 s，最大加速度值为0.75 m/s2，其发生的时刻为3.8 s，土-古城墙整体结构城墙顶部最大位移为17 mm，其发生的时刻为6.7 s，最大加速度值为1.03 m/s2，其发生的时刻为3.85 s.

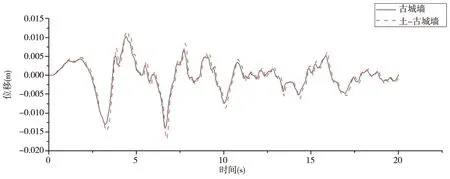
图7 Taft波激励下顶部节点位移对比

3.3 天津波激励下结构反应

由图9、10可以看出，输入修正后的时间20 s的天津地震波，上部结构古城墙顶部最大位移为34 mm，其发生的时刻为7.65 s，最大加速度值为0.91 m/s2，其发生的时刻为7.65 s，土-古城墙整体结构城墙顶部最大位移为40 mm，其发生的时刻为7.7 s，最大加速度值为1.01 m/s2，其发生的时刻为7.7 s.

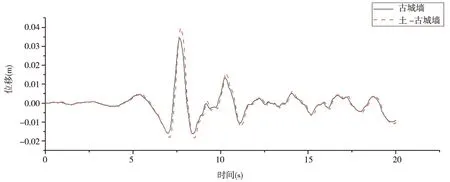
图9 天津波激励下顶部节点位移对比

由表7和5-10图可知，通过数据对比可以得出，存在土层作用时，古城墙模型的位移和加速度反应同时被放大，El-Centro波作用时，整体结构土-古城墙顶部位移是上部结构古城墙模型顶部位移的1.2倍，整体结构土-古城墙顶部动力系数是上部结构古城墙模型顶部动力系数的1.39倍，Taft波作用时，整体结构土-古城墙顶部位移是上部结构古城墙模型顶部位移的1.21倍，整体结构土-古城墙顶部动力系数是上部结构古城墙模型顶部动力系数的1.38倍，天津波作用时，整体结构土-古城墙顶部位移是上部结构古城墙模型顶部位移的1.17倍，整体结构土-古城墙顶部动力系数是上部结构古城墙模型顶部动力系数的1.15倍.

表7 三种地震激励下模型位移和加速度峰值

4 结 论

通过对古城墙和土-古城墙建立两种模型，用有限元进行结构动力特性分析，输入三种地震波激励，得出两种模型的位移和加速度，进行比较研究，得出以下结论：

(1)通过模态分析，分别得到古城墙和土—古城墙两种模型的自振频率和周期，两种模型前三阶振型较为接近，主要是以上部结构振动为主，但是从总体趋势可以看出，土层的存在改变了上部结构的自振特性，主要是下部土层带动上部城墙共同振动，频率减小，周期变大.

(2)在El-Centro波、Taft波、天津波的激励下，分别得到古城墙和土—古城墙两种模型顶部节点的位移和加速度时程，通过比较得以得出，土—古城墙模型的顶部节点位移和加速度均比古城墙模型增大，所以在进行古城墙抗震性能分析的同时，考虑结构与下部土层的相互作用才能使得结构地震时更加安全.