带两对对称平板的圆柱绕流问题研究
张雪娇, 刘官厅,2
(1.内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022;2.内蒙古师范大学 应用数学中心,内蒙古 呼和浩特 010022)
绕流现象是生活生产和工业工程中非常普遍的现象,无论是气体还是液体绕流都会对物体产生一定的影响[1-4]。因此,研究绕流现象具有重要的现实意义。目前,关于圆柱绕流的研究在数值和实验上都有许多成熟的结果[5-8]。此外,人们一直致力于研究具有简单边界的物体绕流。Zhou等[9]对带有上游分流板的圆柱体周围的流动进行了实验研究。纪雪林等[10]对椭圆柱绕流问题进行了分析,得出了椭圆柱周围流场的压强和速度的一些特征。
与圆柱绕流运动相比,带有板的圆柱绕流运动要复杂得多,这是由于板与圆柱之间相互影响,并且板包含端点。本文研究了无粘性不可压缩流体的带有两对对称平板的圆柱绕流运动问题。该模型的实际应用也非常广泛,海底石油钻井平台就是一个典型例子。对于具有复杂边界物体的绕流运动,使用奇点迭代方法和镜像法很难求出此种复杂绕流问题的复势函数。因此,根据复势函数的特征,用复变方法中的保角变换[11]来得出本文所研究问题的复势函数,然后利用复变方法得到速度势函数和流函数。进行对比分析发现本文的研究结果与实际流动非常吻合。
1 问题陈述
速度为V∞、流动冲角为α的无粘性不可压缩均匀流体绕带有两对对称平板的圆柱体流动。圆柱的半径为R,平板的长度分别为a-R和c-R。流体做平面运动,并把该平面看作物理平面z,设在z平面的流动是平面定常无旋的且不考虑环量。流动形式如图1所示,分析该流场的速度和压力分布。
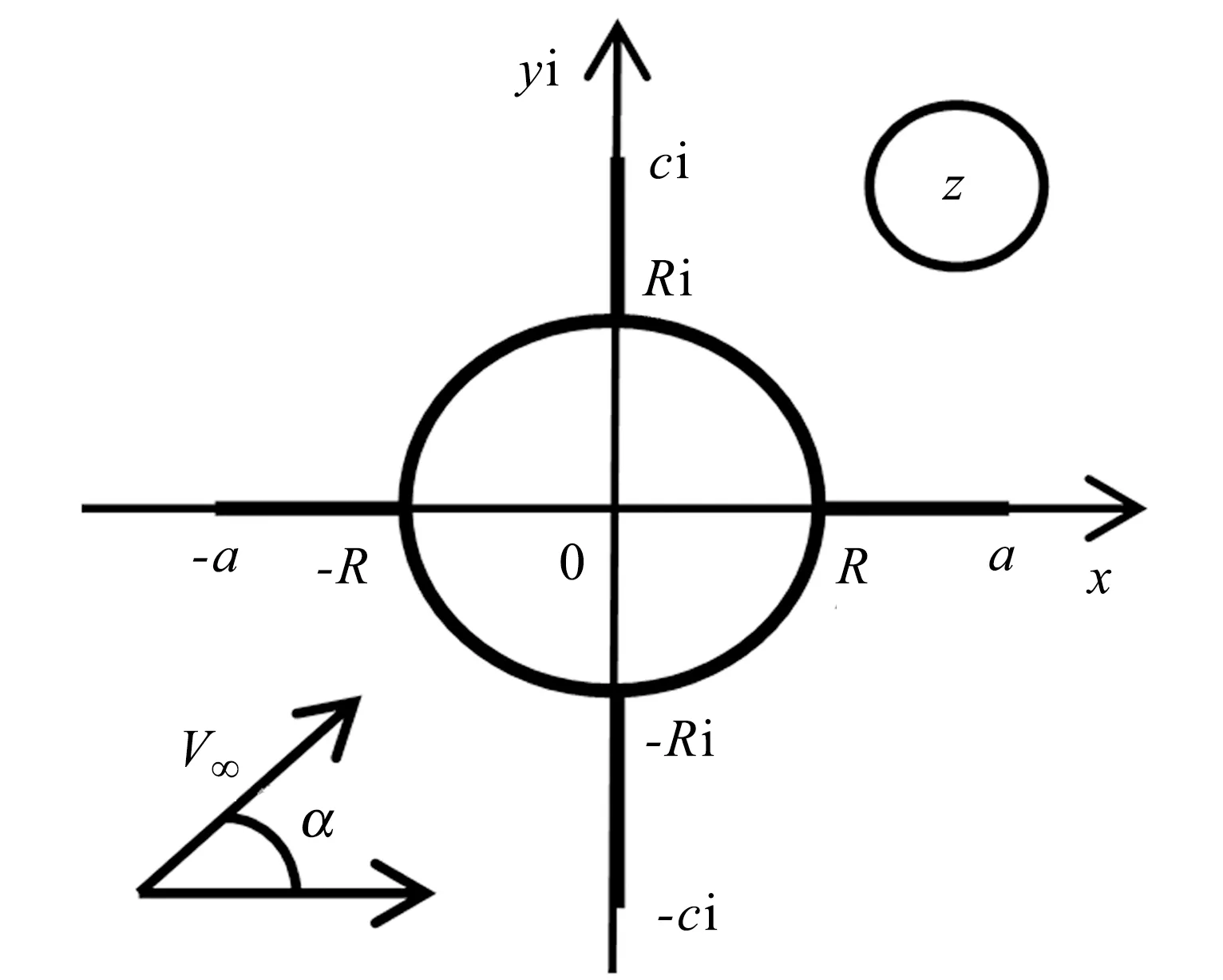
图1 物理平面zFig.1 Physical plane z
2 基本方程
2.1 无粘性不可压缩流体无旋运动的速度势函数
无粘性不可压缩流体的无旋运动是真实流体运动在一定条件下的简化,其研究具有重要的实际意义。无粘性不可压缩流体运动满足连续性方程[12]
divv=0
(1)
和运动方程
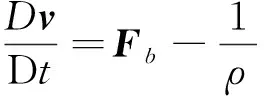
(2)
其中v是流体速度,Fb是质量力,ρ是流体密度,p是流体压强。此外,还应满足边界条件。显然这组方程是非线性的,而且速度和压强耦合,直接求解比较困难。
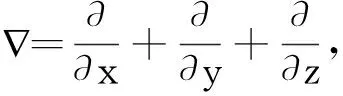
∇2φ=0。
(3)
这是一个拉普拉斯方程,在一定的边界条件下可以求解。对于正压流体和体力有势的情况,当流动无旋时,有拉格朗日积分
(4)
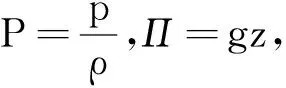
这样,无粘性不可压缩流体无旋运动的基本方程组变为
∇2φ=0,
(5)
(6)
边界条件视具体边界而定。方程(5)是拉普拉斯方程,数学上已有许多方法可求其通解。当流体在流动过程中,各场变量不随z方向发生变化时,其流动可看作是平面流动,本文只讨论平面无旋流动。
2.2 不可压缩流体平面运动的流函数
如果流体做平面运动,取此平面为x-y平面,则连续性方程可以写为[12]
(7)
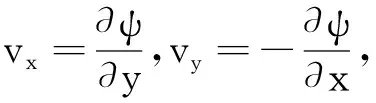
对于平面流动,流体涡量ω只有z轴方向上的分量,记为ω=ωk。从而有ω=-∇2ψk,又可以写为
ω=-∇2ψ。
(8)
且在无旋运动的情况下,方程(8)化为
∇2ψ=0。
(9)
于是,对于本文所讨论的无粘性不可压缩流体的平面无旋运动,流函数ψ(x,y)也满足拉普拉斯方程。
2.3 平面无旋运动的复势
无粘性不可压缩流体的平面无旋运动可以引进速度势函数φ或流函数ψ来求解,且从上述讨论可知道其满足拉普拉斯方程。根据定义,在直角坐标系中有[12]
(10)
即这两个调和函数还满足柯西-黎曼条件。因此它们可以组成一个解析函数,即
W(z)=φ(x,y)+iψ(x,y),
(11)
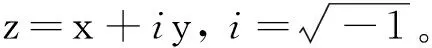
2.4 流场中的速度及压强分布
平面运动流场中任意一点处的流体速度大小为
(12)
流场中任意一点处的压强p可由伯努利方程求出
(13)
其中V∞、p∞、ρ∞分别为均匀来流的速度、压强和密度。此处定义压强系数[12]
(14)
以此来描述流场中的压强分布。
3 带两对对称平板的圆柱绕流问题的解析解
3.1 基本思想
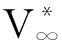
如果C*是半径为r的圆,则ζ平面上的复势函数为[12]
(15)
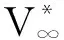
W*(ζ)=W*(F-1(z))=W(z)。
(16)
3.2 保角变换和复势函数
对于图1所示的流动问题,利用如下保角变换[11]
(17)
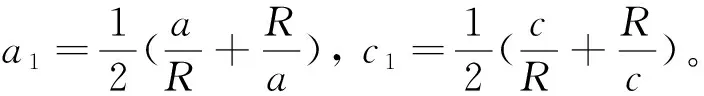
(18)
该逆变换把z平面上带两对对称平板的圆柱的外部区域映射到ζ平面上单位圆的外部区域,如图2所示。
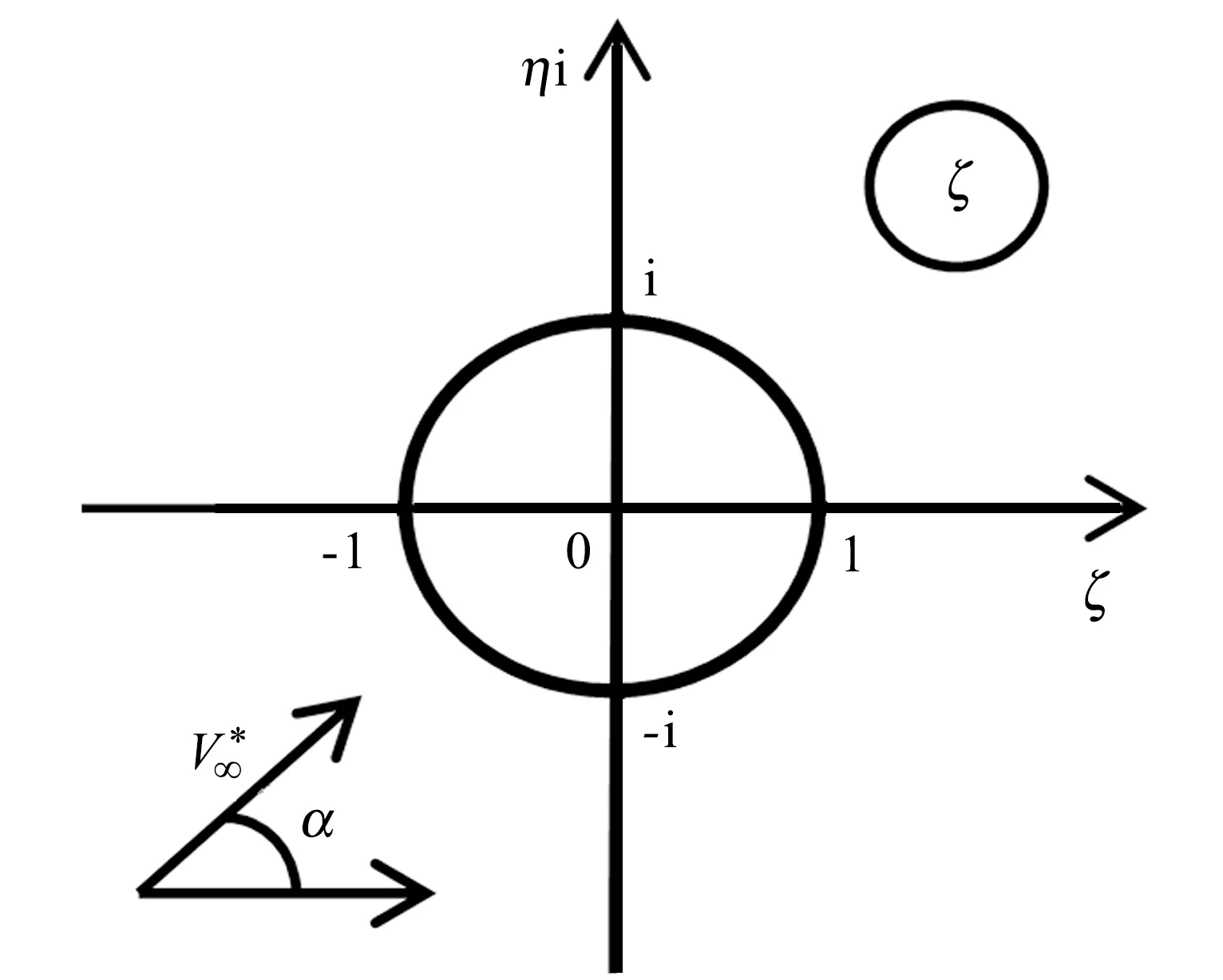
图2 辅助平面ζ Fig.2 Auxiliary plane ζ
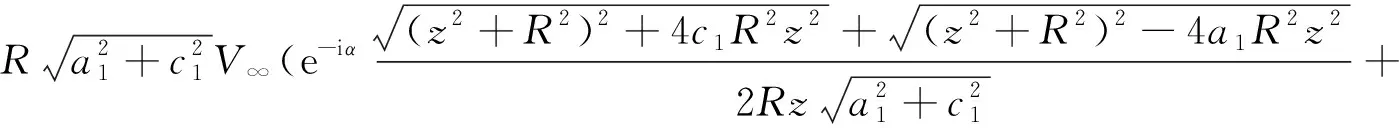
(19)
分离W(z)的实部和虚部,有
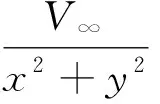
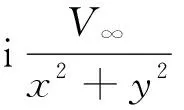
(20)
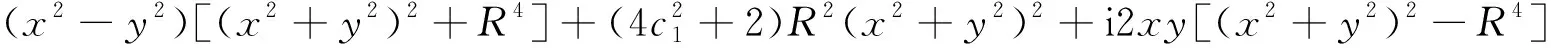
3.3 速度势函数和流函数
从(20)式,可得φ(x,y)和ψ(x,y)分别为
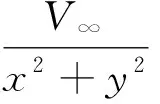
(21)
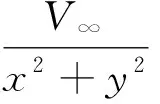
(22)
其中:θ,β,k1和k2与上述相同。由此可见速度势函数φ(x,y)和流函数ψ(x,y)与θ,β,k1和k2是相关的。
根据势函数和流函数的定义,令φ(x,y)=const,可以得到等势线。同理,令ψ(x,y)=const,可以得到流线。再由(12)式-(13)式,根据势函数和流函数可以得到压强系数,并且可以据此分析流场的速度和压强分布。
4 数值算例
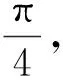
4.1 速度势函数与流函数的计算
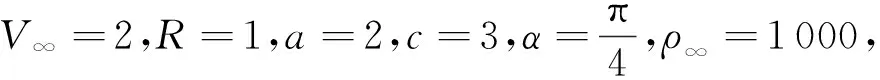
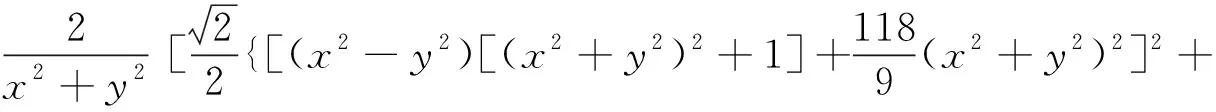
(23)
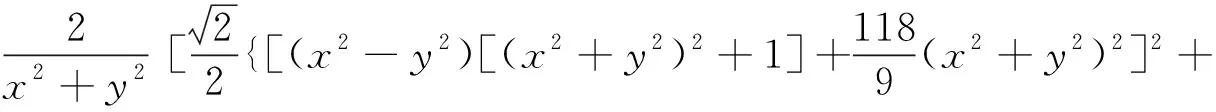
(24)
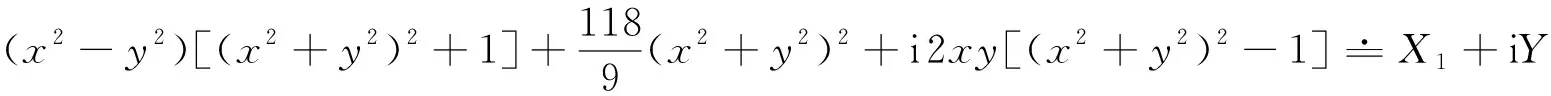
根据θ和β的不同取值,将物理平面z(除圆柱外)分为几个不同区域,如图3所示。

图3 几个不同区域Fig.3 Several different areas
为了保证物理平面z和辅助平面ζ的一一对应,需要对k1和k2的值进行讨论,在区域1至区域5取k1=k2=1,在区域6至区域10取k1=k2=0。
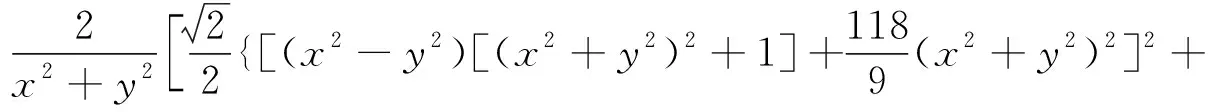
(25)
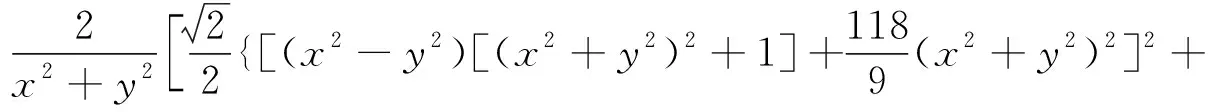
(26)
同理,可以得到其他9个区域的速度势函数和流函数,不再赘述。
4.2 流线图和等势线图
根据每个区域中流函数的表达式,令ψ(x,y)=const并取适当的const值,可以绘制出每个区域的流线图,进而可以得到完整的流线图,如图4所示。类似地,可以得到完整的等势线图,如图5所示。
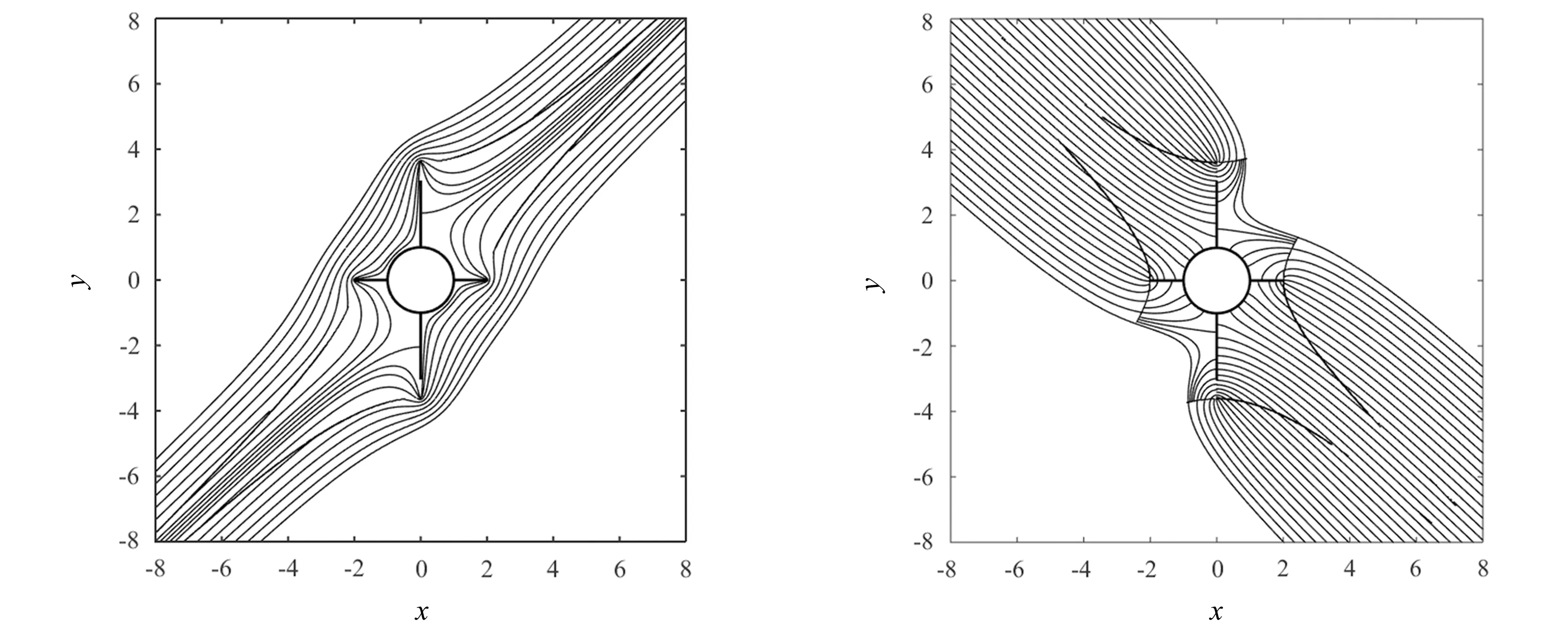
图4 完整流线图 图5 完整等势线图Fig.4 Complete streamline diagram Fig.5 Complete equipotential line diagram
由图4可知,流动情况与实际流动相符,在点(-1,0),(1,0),(0,-i)和(0,i)没有流线通过,因此这四个点处的流体速度为0 m/s。在大约(0,-2.1i)和(0,2.1i)处,流线垂直于竖直方向的平板,因此这两点的流体速度也为0 m/s。这些点称为流场的驻点。流线在(-2,0),(2,0)和大约(0,-3.5 i),(0,3.5 i)点处汇集,因此理论上在这些点处的流体速度是无穷大的,这些点称为流场的奇点。如图5所示,物体附近的等势线垂直于平板,远离物体的等势线逐渐变直。
4.3 压强系数
不同区域的压强系数不相同,从图3可以看出,水平板的下侧在区域7中,因此可以利用区域7的势函数,根据(12)式-(14)式,可以得出位于区域7中的水平板下侧的压强系数为
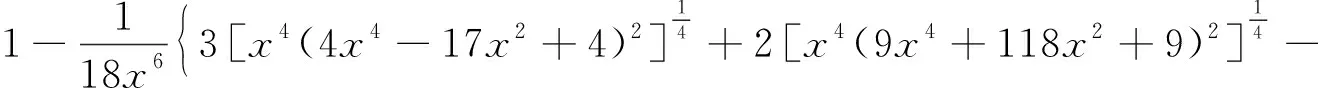
(27)
然后,绘制出区域7中水平板下侧的压强系数图,如图6所示。类似地,可以绘制出区域7中的圆柱表面的压强系数图,如图7所示。
从图6和图7可得,在x=-1和x=0处cp=1,这是cp的最大值。表明压强也达到最大值2 000+p∞,在这里的流体速度是0 m/s。大约在x=-1.77处,cp=0,压强等于p∞,速度等于V∞=2 m/s。在x=-2处,cp=-∞,压强为负无穷大,速度为无穷大。这与流线图反映的流动情况一致。
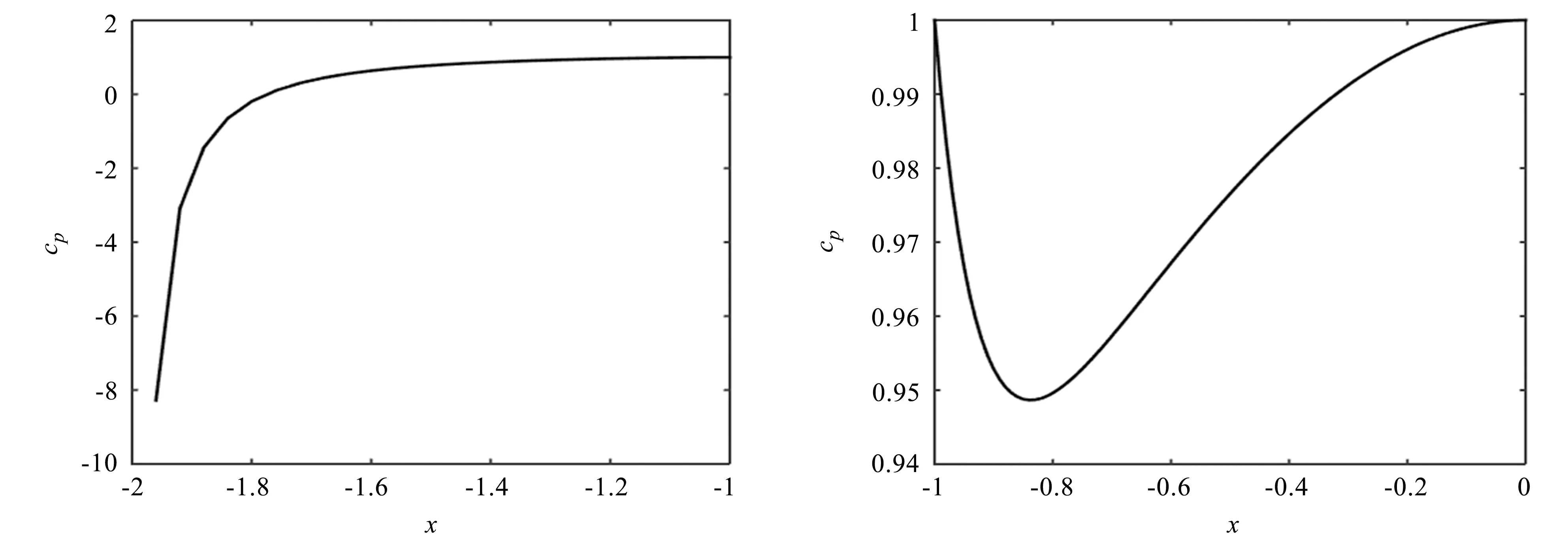
图6 区域7中水平板下侧的压强系数图 图7 区域7中圆柱表面的压强系数图Fig.6 Pressure coefficient diagram of the lower Fig.7 Pressure coefficient diagram of side of the horizontal plate is in area 7 cylindrical surface in the area 7
同理,可得其他区域的压强系数图,进而分析出特殊点处的压强和速度,此处不再赘述。
5 几种流动冲角取其他值的情形
5.1 流动冲角α=0
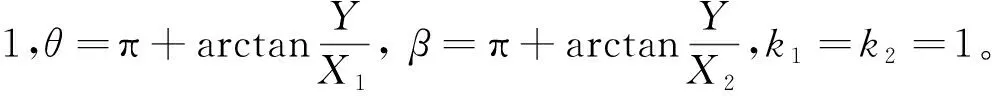
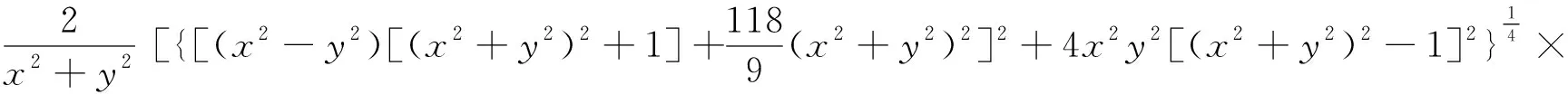
(28)
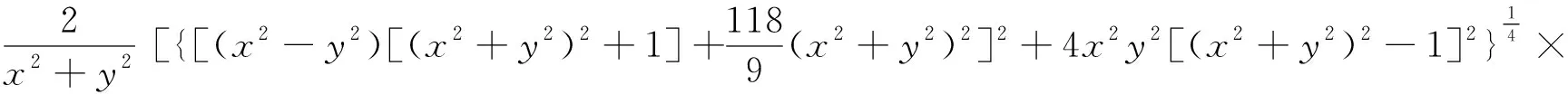
(29)
同理,可得到其他几个区域的速度势函数和流函数,并绘制流线图和等势线图,如图8和图9所示。
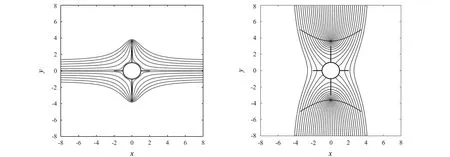
图8 α=0时的流线图 图9 α=0时的等势线图Fig.8 Streamlines diagram of α=0 Fig.9 Equipotential lines diagram of α=0
如图8、图9所示,在这种情况下,水平平板对流场没有影响。在点(-1,0),(1,0),(0,-i)和(0,i)没有流线经过,这四个点的流体速度为0 m/s。在点(-2,0)和(2,0)处,流线垂直于水平平板,这两点的流体速度也为0 m/s,这些点称为流场的驻点。流线在(0,-3.5 i)和(0,3.5 i)处汇集,理论上在这些点处的流体速度是无穷大的,这些点称为流场的奇点。
利用相同的方法,绘制区域7和区域9中y轴左侧和圆柱表面的压强系数图,如图10所示。
根据图10(a)和(c),并结合计算,可知大约在y=±3.6处,cp取最小值负无穷大,这表明此处的速度为无穷大,压强为负无穷大。通过图10(b),可知在y=0和y=±1处,cp取最大值1,此时压强也取最大值2 000+p∞,流体速度为0 m/s。这与流线图中的结果一致。
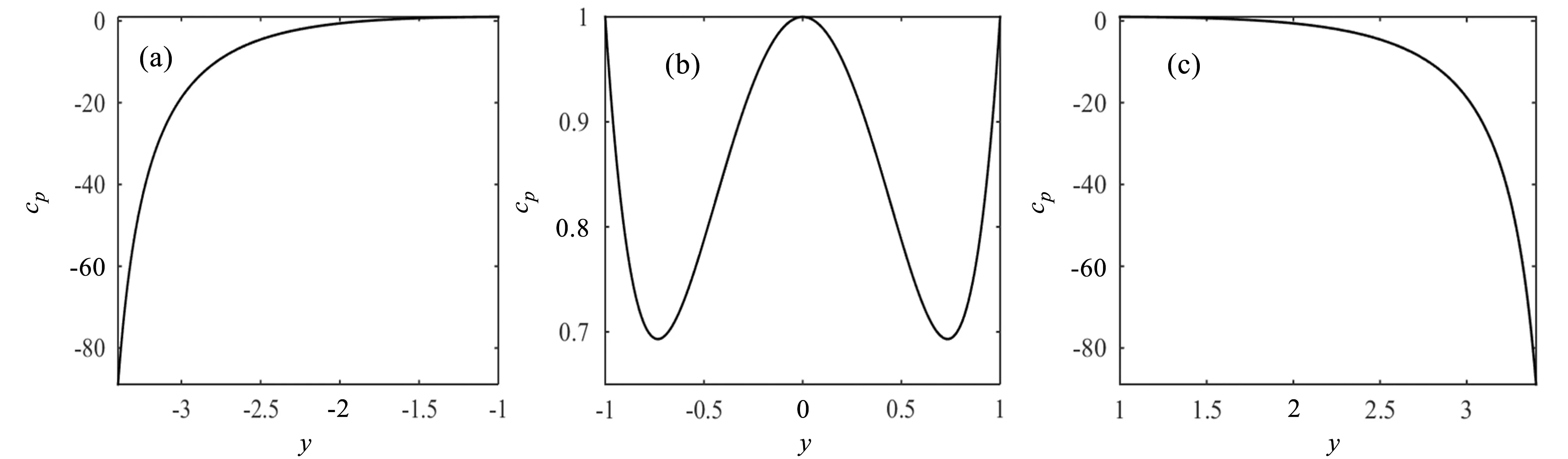
图10 区域7和区域9中的压强系数图Fig.10 Pressure coefficient diagram in regions 7 and 9
5.2 流动冲角
与上述算例相同,这种情形下区域1中的速度势函数和流函数分别为
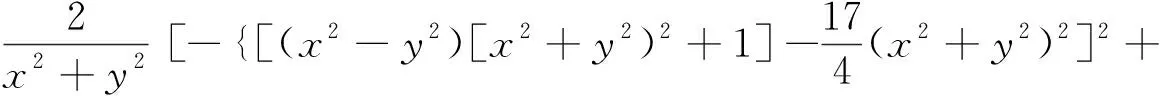
(30)
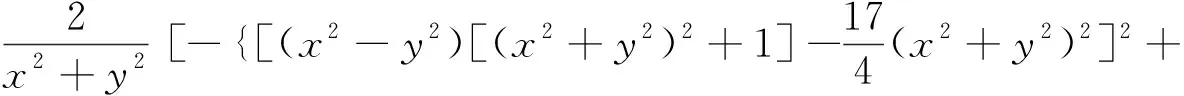
(31)
流线图和等势线图如图11-图12所示。流线图中,在点(-1,0),(1,0),(0,-1)和(0,1)处没有流线,表明当流体流过这些点时,流体速度等于0 m/s。在(0,-3 i)和(0,3 i)处,流线垂直于竖直平板,这两点的流体速度也为0 m/s,这些点称为流场的驻点。在(-2,0)和(2,0)处流线汇集,此处的流体速度等于无穷大,这两个点称为流场的奇点。流动形式与实际情况相符。
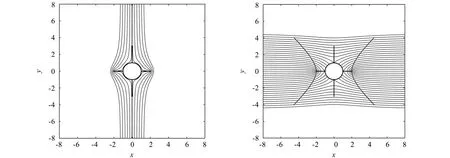
图11 α=π/2时的流线图 图12 α=π/2时的等势线图 Fig.11 Streamlines diagram at α=π/2 Fig.12 Equipotential lines at α=π/2
区域4和区域7中的平板和圆柱表面的压强系数如图13所示。从图13(a)可知,在x=-2处,cp=-∞,这表明此处的流体速度为无穷大,压强为负无穷大。从图13(b)可知,在x=±1和x=0处,cp=1,这是cp的最大值。此处压强也取最大值2 000+p∞,流体速度为0 m/s。这与流线图中的结果一致。
6 十字型平板绕流问题
6.1 保角变换、速度势函数和流函数
下面研究无粘性不可压均匀流体的十字型平板绕流问题。流动形式如图14所示。
保角映射退化为
(32)
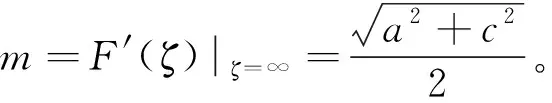
(32)式的逆映射为
(33)
该逆映射把十字型平板外部区域映射到单位圆外部区域,如图15所示。
(34)
分离W(z)的实部和虚部,得到速度势函数和流函数如下
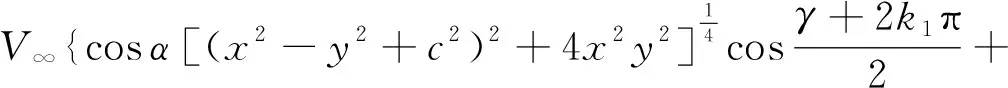
(35)
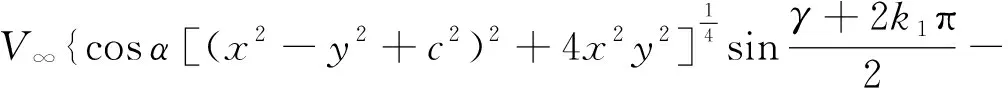
(36)
其中γ是(x2-y2+c2)+i2xy的辐角,k1=0或1。λ是(x2-y2-a2)+i2xy的辐角,k2=0或1。
6.2 数值算例
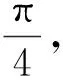
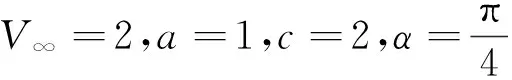
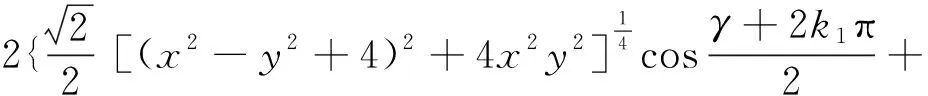
(37)
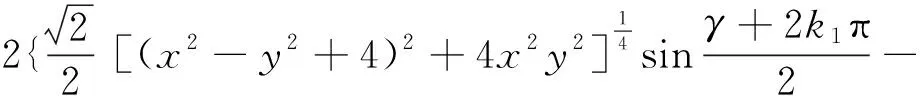
(38)
其中:γ是(x2-y2+4)+i 2xy≐X1′+iY′的辐角,k1=0或1;λ是(x2-y2-1)+i 2xy≐X2′+iY′的
辐角,k2=0或1。根据γ和λ的不同取值,将平面分成如图16所示的几个区域,并且在区域1-区域5令k1=k2=1,在区域6-区域10令k1=k2=0。
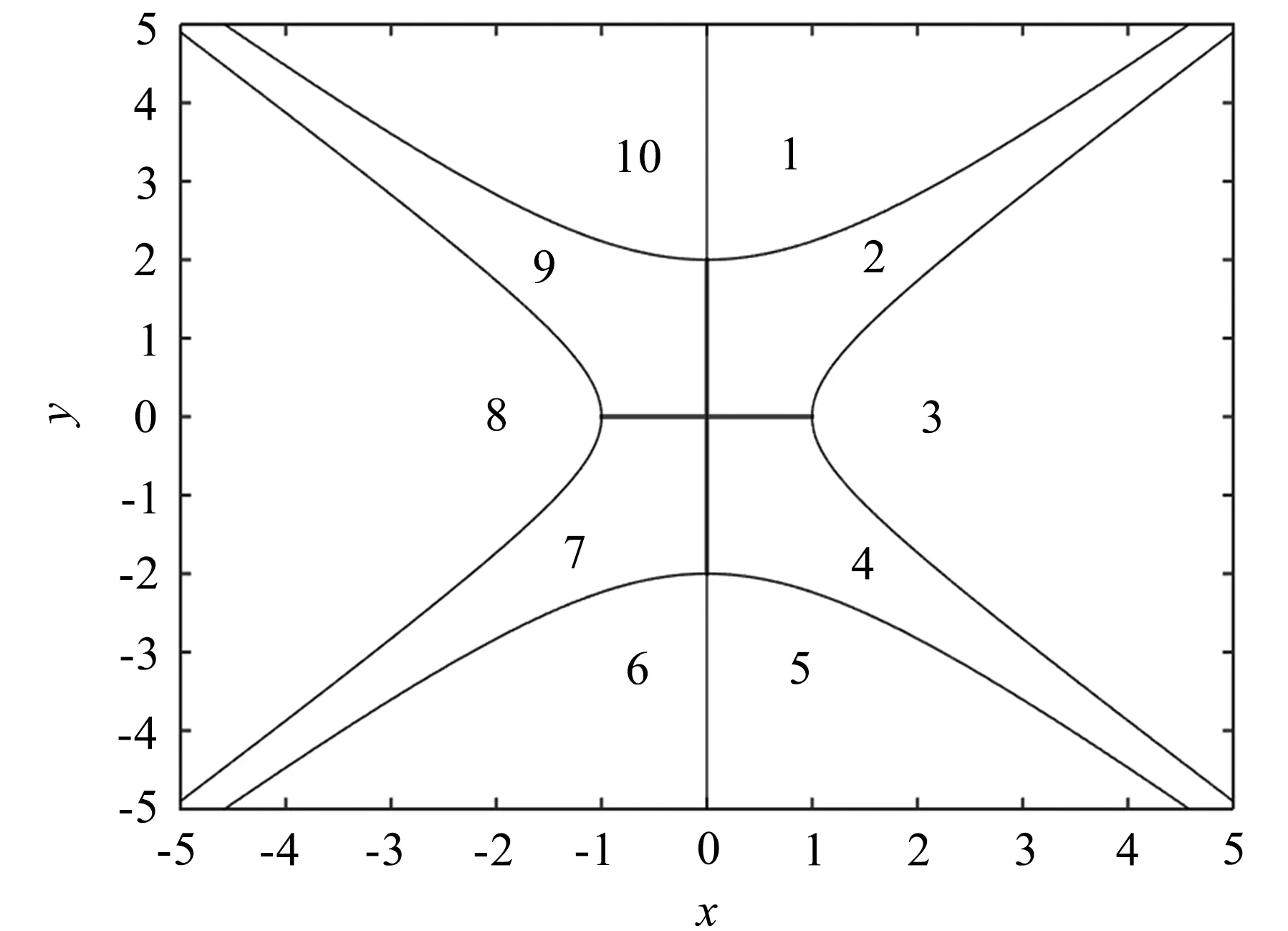
图16 不同区域Fig.16 Different regions
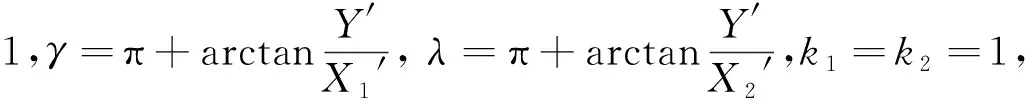
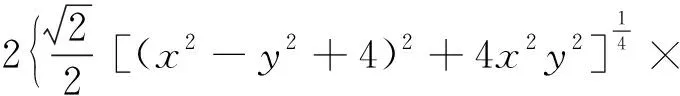
(39)
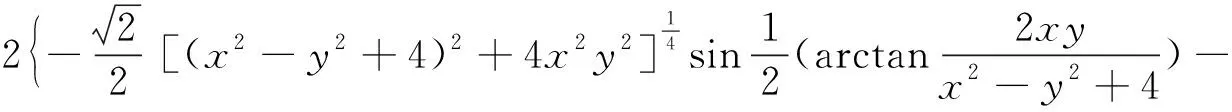
(40)
同理,还可以得出其他区域的速度势函数和流函数,并绘制出流线图和等势线图,如图17和图18所示。如流线图所示,原点处不存在流线,并且在(0,-1.25 i)和(0,1.25 i)处流线垂直于平板,因此这三个点处的流体速度均为0 m/s。在(-1,0),(1,0),(0,-2 i)和(0,2 i)处流线汇集,这表示此处的流体速度等于无穷大。
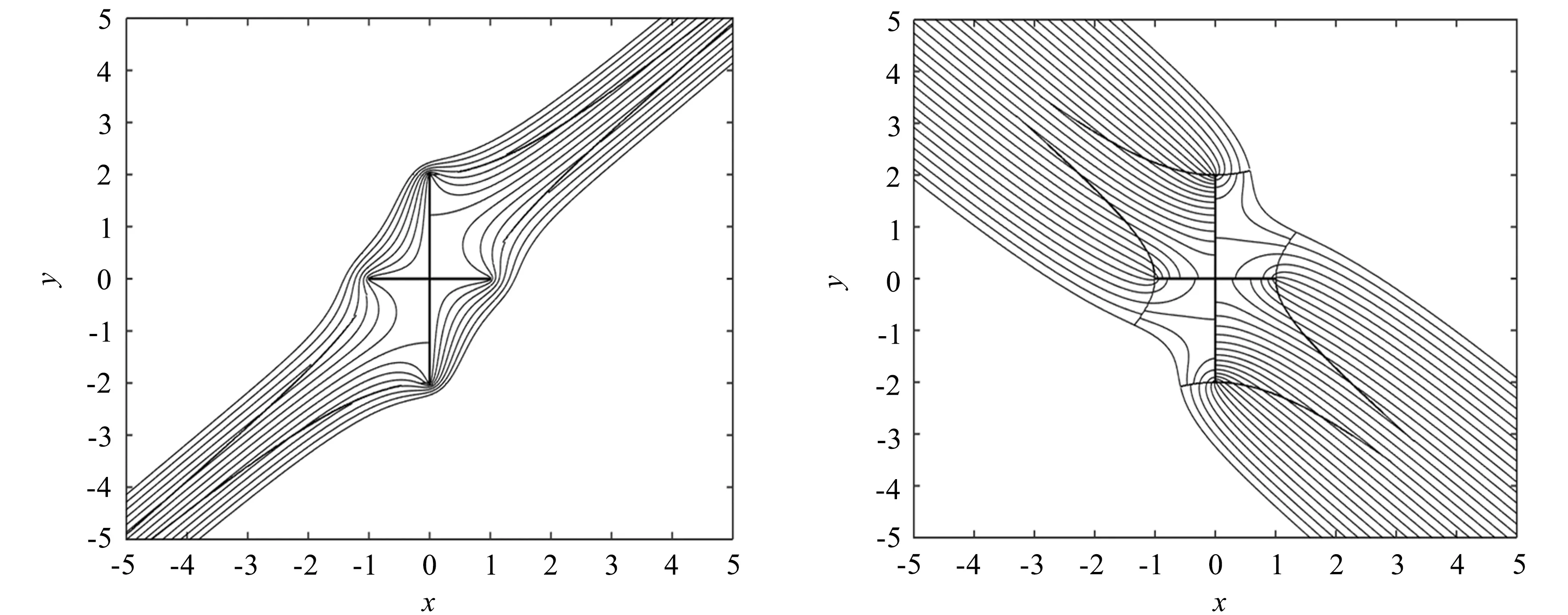
图17 流线图 图18 等势线图Fig.17 Streamline diagram Fig.18 Equipotential line diagram
区域7中物体表面的压强系数如图19所示,在x=-1处,cp=-∞,这表明此处流体速度为无穷大,压强为负无穷大。在x=0处,cp=1,这是cp的最大值。此处压强也达到最大值2 000+p∞,速度为0 m/s。这些均与流线图的结果一致。
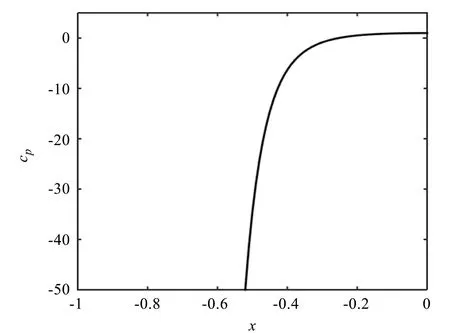
图19 区域7中水平平板的压强系数图Fig.19 Pressure coefficient diagram of horizontal plate in area 7
7 结论
本文通过共形映射方法,研究了无粘性不可压缩均匀流体绕带两对对称平板的圆柱和十字型平板流动的问题。可以得到以下结果:
(1) 在流场驻点处,流体速度为0,压强达到最大值;
(2) 在流场奇点处,流体速度是无穷大,压强是负无穷大;
(3) 当均匀来流的方向平行于平板时,平板对流场无影响;
(4) 不同的流动冲角对压强系数的影响不同,对流场中压强和速度的影响也不同。
这些结果为后续研究提供了理论基础,从流线图和等势线图可以看出,本文的流动情况与实际流动情形吻合较好。

