基于小波相干的“碳中和”概念股联动研究

陈德财, 米宇平,2, 王桂霞,2, 张宏坤

(1.内蒙古师范大学 数学科学学院,内蒙古 呼和浩特010022;2.内蒙古师范大学 应用数学中心,内蒙古 呼和浩特 010022;3.美国马萨诸塞大学 数学与统计学院,马萨诸塞 阿默斯特 01003)

自2020年9月中国在联合国大会上提出“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”的目标后,“碳达峰、碳中和”成为整个社会关注的焦点。2021年3月,中央财经委员会第九次会议研究了促进平台经济健康发展问题和实现碳达峰、碳中和的基本思路和主要举措,这为“碳中和”概念股带来新的机遇和挑战。在碳中和背景下,企业生产经营活动带来的碳排放量、碳减排措施等信息将引起国内外投资者和相关机构广泛关注,国家政策的推进和公众意识的提高使企业碳信息直接影响到企业财务绩效。数据显示,2021年3月16日,中材节能、深圳能源等龙头股由绿盘翻红,碳中和主线不断爆发,并继续扩散,碳中和龙头呼之欲出,碳中和各概念股的走势是否存在联动效应值得研究探讨。

对联动效应及相关性的研究方法由常相关到动态相关、一元到多元、线性模型到非线性模型,特别是GARCH模型族和Copula理论的提出和应用,极大地促进了该问题的研究,但这些方法不涉及频域,一般是针对时间维度进行分析。而小波分析多尺度分解方法在时频域的分析效果良好。

本文选取2017年9月1日至2021年4月13日国内5支不同类别、不同行业“碳中和”概念股,包括深圳能源(公用事业)、中泰化学(化工)、东珠生态(环保工程及服务行业)、华测检测(综合III)及中材节能(技术服务),以各股的日数据作为样本,每只股票时间序列的数据皆为877个。通过连续小波变换分析说明各股价格指数的波动情况,进一步用互谱小波分析实证各股价格指数间的相干性,旨在跟踪龙头股并分析龙头股对其余股票的联动效应。

1 预备知识

从宏观上看,小波变换[1-6]具有良好的时频局部化特性,可使多自由度系统的模态自动解耦,因而被广泛应用于结构模态参数识别领域。

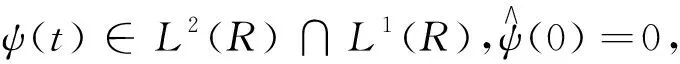
(1)

称{ψa,b(t)}a,b为连续小波,相应地称ψ(t)为小波函数或母小波,其中,a为尺度因子,b为平移因子。ψa,b(t)也常称为连续小波基函数,变量a反映了函数的宽度,变量b检测小波函数在t轴上的平移位置。

常见的小波基有十多种,由于小波基不具有唯一性,对同一信号采用不同小波基处理的结果有一定差别,因此利用股票时间序列数据进行多尺度小波变换时,小波基的选取很重要。Morlet小波是一种连续小波,作为小波母函数,是一个周期函数,并且是高斯包络下的单频率复正弦函数,其不但克服了离散小波在时间域上对信号离散化所造成的特征信息遗漏现象,而且还克服了二进小波变换在尺度空间上二进分割过于粗糙的情况。Morlet小波具有良好的时间聚集性、较高的频率分辨率、包含相位信息等特点,因此被广泛应用于分析两个非平稳时间序列的关联性。

定义2[2,7](连续小波变换) 假设函数ψ(t)为一个母小波,ψa,b(t)由(1)式定义,信号s(t)∈L2(R)的连续小波变换为

(2)

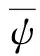
(2)式的离散形式为

(3)

(4)

(5)

其中:s代表平移尺度;δt代表对数据的采样频率;sj为平移尺度的具体取值情况;N为时间序列的长度。对(3)式进行取模运算,即可得到小波功率谱,小波功率谱表达了时间序列在给定小波尺度和时间域内的波动量级。

定义3[7](Morlet小波) Morlet小波在时域上的表达式为

(6)

在频域上的表达式为

(7)

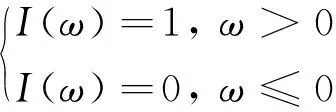
(8)

是一个指示函数。(7)式最终为关于ω的函数。

若无特殊说明,在进行连续小波变换时,本文皆取δt=1/12,α=12,ω0=6。

通过连续小波变换(CWT),可以将多自由度系统的自由响应分解为各个单自由度系统的自由响应,从每个单自由度对应的小波系数中可获得各阶模态的频率和阻尼比。

定义4[8](小波相干谱)

(9)

基于小波相干谱,定义

(10)

为中心权重矩阵[8];

(11)

为中心权重表达式[8]。

定义5[9-11](相位差) 定义

(12)

为各尺度成分之间的相位差[7,9-11]。通过变量之间相位差可以了解变量之间的相干性。

若无特殊说明,在进行连续小波变换时,本文皆取δt=1/12,α=12,ω0=6。

2 数据分析

若无特殊说明,本文所有插图中时间序号对应的时间见表1。所选5只股票2017年9月1日至2021年4月13日的时间序列可视化结果如图1。

图1 所选5股的可视化结果Fig.1 Visualization of selected 5 stocks

表1 时间序号与具体时间的对应关系Tab.1 The corresponding relationship between serial number of time and specific time

2.1 股票波动分析

对所选股票分别进行连续小波变换,连续小波变换功率谱图如图2至图6所示。图中横坐标代表时间,纵坐标代表周期T=1/f,即对应频域的倒数。

图2后半段块状区域较多,但面积较小,纵坐标对应的数值也比较小,说明该股有过短期波动,但持续时间不长。表明深圳能源股的整体波动不大。其原因之一是受到了国家政策的影响,中国在2020年9月提出了碳中和政策,且实现的主要方式是植树造林、开发新能源和节能减排等,深圳能源集团的主要业务是新能源开发,在2020年9月以后得到了国家项目支持。

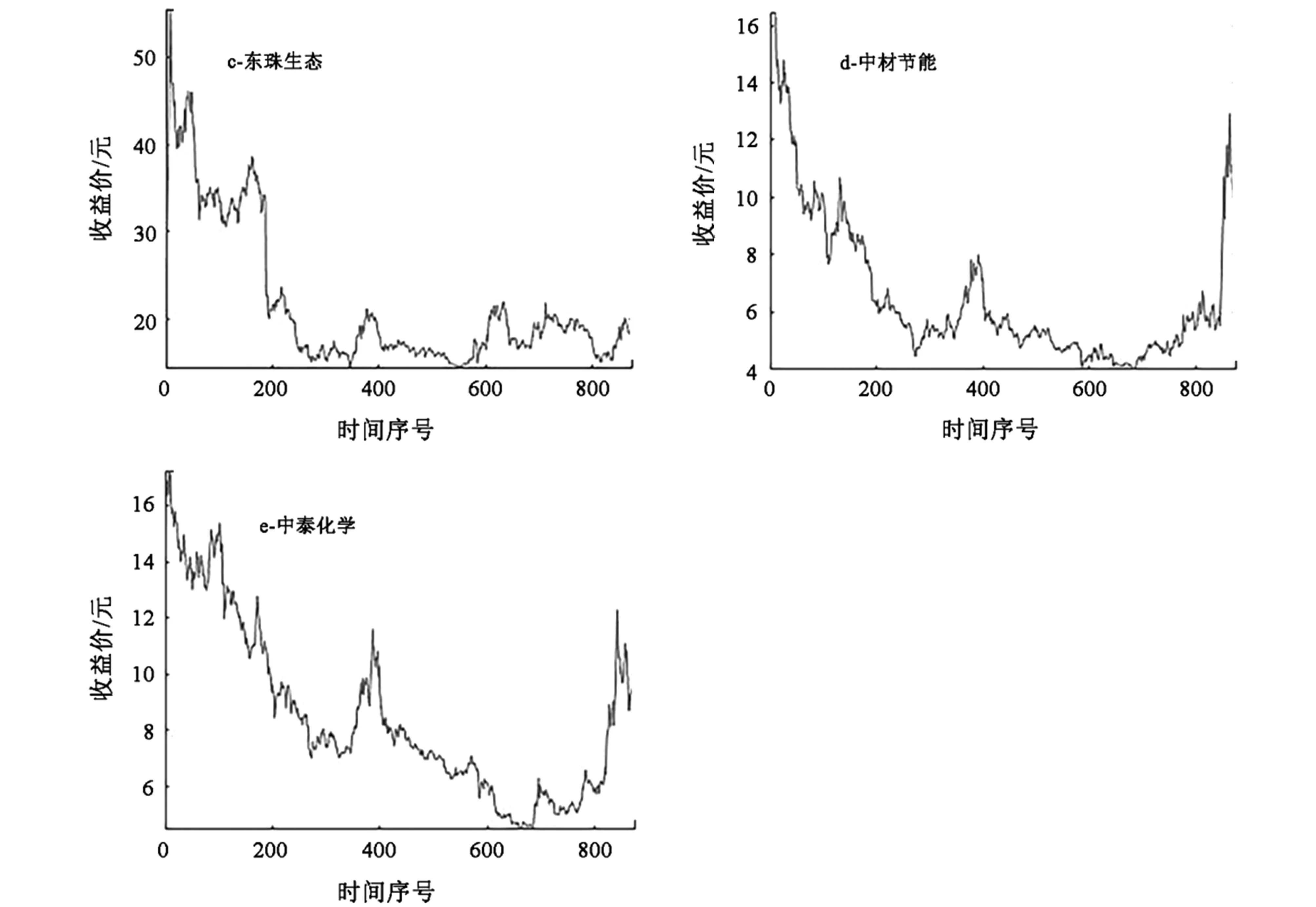
续图1 所选5股的可视化结果Continued Fig.1 Visualization of selected 5 stocks

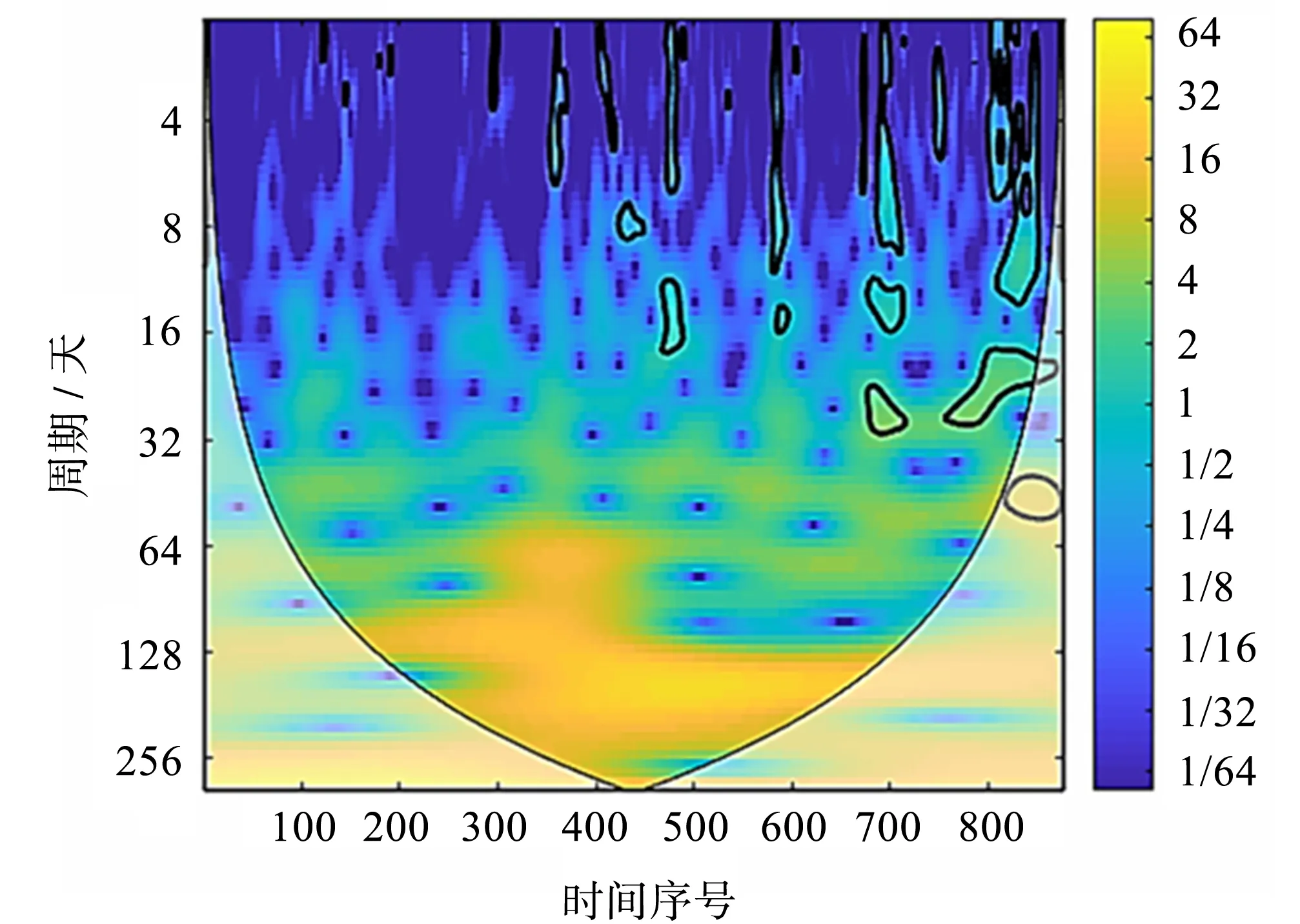
图2 深圳能源CWT小波功率谱图Fig.2 CWT wavelet power spectrum of Shenzhen Energy

图3和图4中上部都出现了一些不规则块状区域。特别是2020年7月以后,图4的不规则块状区域数量明显增多。此外,中泰化学有一处颜色较深的不规则块状区域。这表明中材节能股和中泰化学股虽然整体波动不大,但比较而言,中泰化学比中材节能波动明显。2020年7月以后中材节能不规则块状区域增多的原因之一是中材节能集团主要在工业节能、建筑节能、能源综合管理及环保服务等领域为客户提供技术、工程和投资服务节能服务,符合节能减排要求,得到国家支持和投资者信赖。

图3 中材节能CWT小波功率谱图 图4 中泰化学CWT小波功率谱图Fig.3 CWT wavelet power spectrum of Fig.4 CWT wavelet power spectrum of Sinoma Energy Saving Sino Thai Chemical

图5内不规则区域对应的纵坐标数值较大,图6内不规则块状区域分布在上部,纵坐标对应的数值较小,这一结果表明东珠生态股的波动性较强且持续时间较长,整体表现不稳定,而以检测、认证、审核、培训服务为主的华测测股表现平稳。

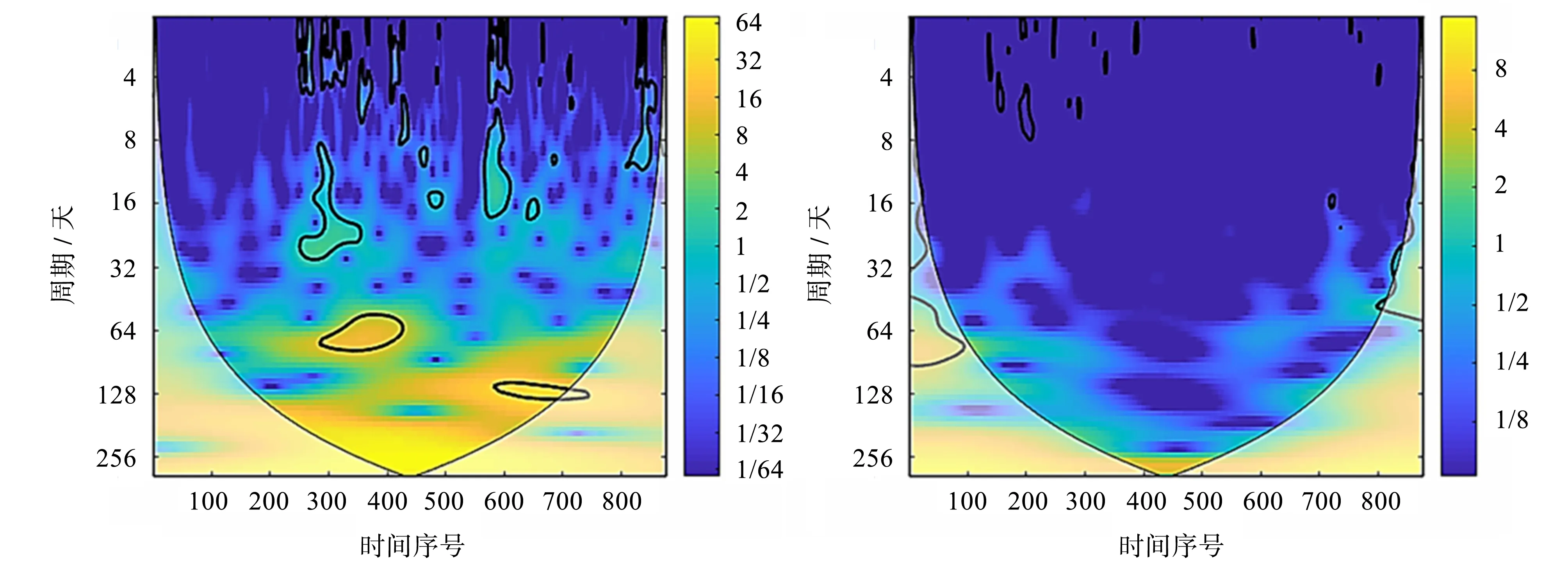
图5 东珠生态CWT小波功率谱图 图6 华测检测CWT小波功率谱图Fig.5 CWT wavelet power spectrum of Fig.6 CWT wavelet power spectrum of Dongzhu Ecology Centre Testing International

2.2 小波相干性分析

本节对5只股票时间序列进行DWT(离散的小波变换)及去噪处理,对处理后的数据进行尺度为5的CWT(连续小波变换),利用(9)式-(11)式求出以上5只股票中心权重,确定权重值最大的是深圳能源股。深圳能源权重最大的原因有: (1) 受燃料成本降低的影响,火力发电主营业务利润同比上升; (2) 因新项目投产,固废处理项目利润同比增加; (3) 因南油工业小区拆迁补偿款,营业外收入大幅增加; (4) 2020年8月将迎来深圳特区建立40周年,为了致敬深圳改革开放历史性成就,将会对杰出公司进行政策扶持。

将深圳能源集团的权重曲线与其余集团股票分别进行对比,结果如图7至图10。

图7 深圳能源与东珠生态数据权重对比图 图8 深圳能源与华测检测数据权重对比图 Fig.7 Comparison chart of data weight of Shenzhen Fig.8 Comparison chart of data weight of Shenzhen Energy and Dongzhu Ecology Energy and Centre Testing International

图9 深圳能源与中材节能数据权重对比图 图10 深圳能源与中泰化学数据权重对比图 Fig.9 Comparison chart of data weight of Shenzhen Fig.10 Comparison chart of data weight of Shenzhen Energy and Sinoma Energy Saving Energy and Sino Thai Chemical

结合深圳能源集团2017-2020年的企业年报,可以发现其清洁能源占总公司能源的60%,具有持久的环境保护价值和市场竞争优势。近些年来,深圳能源积极探索新能源业绩良好。

利用(9)式和(12)式分别计算深圳能源股和其余4只股票小波相干值、联动性和差异性,结果如图11至图14。图中横轴代表时间,纵轴代表周期,具体相关系数值由图中右例的颜色对比条给出。

由图11至图12可以发现在漏斗状区域内不规则块状区域较多,说明深圳能源与这2只股票相干性较高,但仍有小一部分区域颜色呈现冷色,说明深圳能源股票与这2只股票在该区域联动程度不显著。图中,大部分块状区域的箭头朝向右方,且角度位于[-π/2,π/2]之间,说明深圳能源与这2只股票的相位差较小,会保持同相运动。

图13不规则块状区域数量最多,且面积最大,说明深圳能源与中材节能集团的相干性最大,而且该时间段内的不规则区域的箭头指向右,与横坐标偏差小,全部在 [-π/2,π/2] 之间,说明在国家政策影响下,中材节能与深圳能源基本同步前进。图14中不规则块状区域较少,说明深圳能源与华测检测的相干性最弱,这是因为华测检测受政策影响较弱,不规则块状区域的箭头角度大部分在 [-π/2,π/2] 之间,说明几段时间内深圳能源与华测检测同相运动。

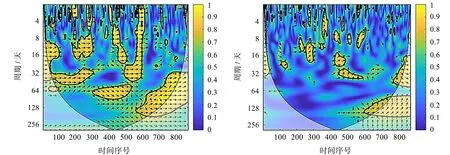
图13 深圳能源与中材节能 图14 深圳能源与华测检测 Fig.13 Shenzhen Energy and Sinoma Energy Saving Fig.14 Shenzhen Energy and Centre Testing International

3 总结

本文选择Morlet小波作为母小波,通过设定相应参数,对五组数据进行连续小波变换,根据中心权重公式确定了影响最大的碳中和概念股; 利用连续小波变换功率谱,讨论了各股波动情况; 基于小波相干和小波相位差同时分别在时频两域定量分析了证券市场碳中和概念股各股间收益率的联动效应。该工作为更大范围内甄别与碳中和相关的碳中和概念股以及确定概念股中的“龙头”,树立在碳中和中起到示范引领作用的标杆企业提供科学的方法。

通过小波相干和小波相位差的对比分析得到了一致的结论:

(1) 深圳能源与华测检测在大部分时频空间上不存在显著的联动效应,图中纵坐标较大的不规则块状区域较少,在几段时间内华测检测会与深圳能源同相运动;

(2) 深圳能源与东珠生态及中泰化学的联动性较强,图中漏斗形以内,不规则块状区域数量较多,深圳能源与东珠生态及中泰化学同相运动;

(3) 深圳能源与中材节能在绝大部分时频空间内存在显著的联动效应,图中漏斗形以内,不规则块状区域数量最多,面积最大,且不规则区域的箭头指向右,与横坐标偏差小,全部在 [-π/2,π/2] 之间,中材节能与深圳能源基本同步前进。