滚动转子压缩机排气流噪声数值计算与机理分析

李天宇，蒋伟康，王海军

（1.上海交通大学 振动冲击噪声研究所，上海 200240；2.上海海立电器有限公司，上海 201206）

0 引言

滚动转子式压缩机作为家用空调和其它小型制冷设备常用的制冷压缩机［1］，其压缩机主体内噪声源主要分为气流噪声、电机噪声和机械噪声。其中气流噪声由冷媒在压缩机内的压力脉动引起，其产生的不良噪声影响到低中高等较宽的频率范围，而且其不仅影响压缩机本身的噪声，还会沿冷媒管道传播从而导致空调室内机的异常噪声，形成空调客户尤为关注的“传递声”。

在传统的关于滚动转子压缩机排气阶段气流噪声分析中，人们一般根据噪声产生的不同结构将其分为涡流噪声、喷射噪声、冲击噪声、旋转噪声和共鸣噪声等［2］。然而这些不同种类的噪声在声源机理上互相有重合之处，同时我们缺乏定量的方法分析它们各自对整体噪声的贡献度和特性。对压缩机主要噪声源机理的认识将有助于提出针对性的降噪方案。

流体力学数值方法日趋成熟，CFD逐渐应用于研究压缩机压力脉动。例如黄曌宇［3］通过大涡模拟（LES）方法计算排气压力脉动并与试验结果对比，得到了压力脉动的主要频率峰值；JANG 等［4-7］使用 CFD 针对不同的气道设计，计算了压缩机内的压力脉动，用以优化排气通道。

目前，对于压缩机CFD计算所聚焦于流场和压力脉动分析，但对于压力脉动和流场与气动噪声关系，尚未有一致认识，为了研究压缩机排气压力脉动的机理和主要成分，本文使用CFD结合声学有限元方法，对某型号滚动转子压缩机排气过程进行了气动声学分析。

1 排气过程的物理模型及分析方法

本文研究使用的样机为一款单缸立式滚动转子压缩机，结构如图1所示，其使用R32作为冷媒，选取工况的转速为3 600 r/min。其内部流动通道复杂，排气过程流经区域可分为泵腔、消声器空腔、电机前腔、定转子通流气隙和电机后腔。研究所关注的频段为5 000 Hz以下。

图1 样机剖面Fig.1 Profile of the prototype

假设流动为单相，压缩机内的冷媒流动和噪声传播都由Navier-Stokes方程描述为：

在压缩机内，冷媒自储液器管道吸入，经泵腔压缩，温度急剧升高。随后在排气通道内，经过多级空腔膨胀，其温度也随压力波动和湍流传热而变化。将工质的状态方程写作密度与压力P和熵s的关系式，由热力学状态函数之间的微分关系可得出：

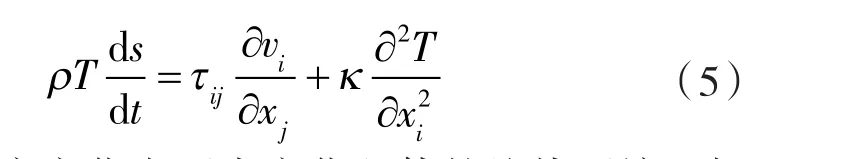
式中 α——热膨胀系数；

cp——等压热容；

μeff—— 考虑湍流涡黏性的有效黏性系数，μeff= μ+ μt；

U——流场内流速尺度；

L——压缩机部件的特征尺寸；

κeff—— 考虑湍流传热的有效热导率，κeff= κ+ κt；

T0——排气温度。

研究所用冷媒的普朗特数Pr约为1，而湍流普朗特数Prt也在同一量级。基于式（6）的保守估计，在计算中将使用等熵假设即可满足对压力脉动的计算要求，从而不引入温度或焓等热力学量。这样做的优点是在没有因为简化物理模型而使关心的物理量（速度和压力）产生较大偏差的前提下，不需要求解能量方程，从而既能节省计算时间，同时也避免了温度或焓因为边界条件或网格质量等问题难收敛的情况。在排气温度和压力附近状态方程可等熵线性近似成：

式中 c——声速。

将式（7）代入式（1）和（2）中并忽略黏滞应力τij后可得到Curle方程为：

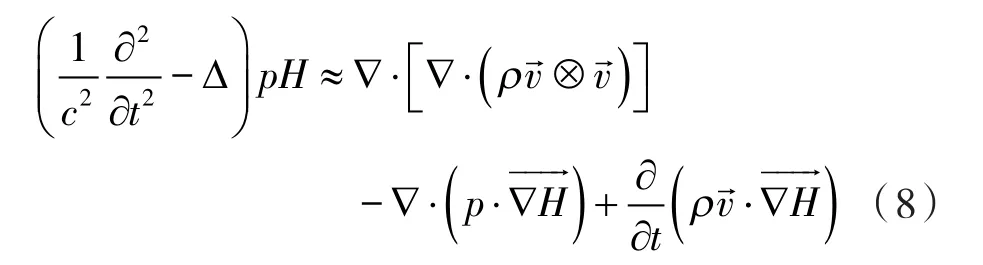
式中 H—— 指示计算实体区域内部的Heaviside函数。

等式右边3项分别表示脉动速度产生的四极子声源、壁面脉动压力产生的偶极子声源和入口质量流入产生的单极子声源。

2 排气过程的气动声学数值模拟

可压缩CFD计算使用商业求解器STARCCM+完成，计算区域为从消声器入口至压缩机出口排气通道，其中转子附近区域使用滑移网格方法以额定转速旋转，且忽略排气阀片的存在。计算采用基于SST k-ω的分离涡模拟（DES）方法作为瞬态湍流计算模型［8］，压缩机出口延伸一定长度设置平均压力出口边界条件，消声器入口以一个通过简单绝热压缩热力学计算得到的类似三角波的质量流率曲线作为入口边界条件。

为了能够有效地捕捉湍流涡结构和声波，数值求解式（1）（2）（7）使用二阶 SIMPLE 格式，对流离散格式为混合二阶迎风/有界中心差分。网格采用多面体单元，单元总数约300万，平均尺寸Δx约1 mm，满足在最高目标频率下每波长内离散点数 PPW=c/（fmaxΔx）＞20。时间步长Δt为0.2CAD（曲轴转角），可以满足声学CFL数cΔx/Δt＜1。该配置比较适合近场低频段的气动噪声求解［9］。

2.1 压力脉动性质分析

CFD计算获得的流场如图2所示，可以发现除消声器、转子和压缩机出口管道内流速较高外，腔内其他部位的流速较低。其中上部空腔内由于冷媒从转子随转动甩出而形成绕腔体周向流动的涡。

图2 排气时刻流线Fig.2 Flow lines at the moment of exhaust

由于湍流脉动导致的四极子体声源功率与脉动速度对应马赫数8次方成正比，壁面偶极子声源功率与脉动速度对应马赫数6次方成正比，因此在电机前后腔内因湍流马赫数小于0.01，其作为噪声源产生的声压远远小于因流动变化产生的湍流压力［10-11］；通过选取机内离中心不同测点观察其压力与速度变化的相关性，如图3，4所示。

图3 3个周期内电机后腔测点压力脉动Fig.3 Pressure fluctuation at measuring points on rear chamber of the motor within 3 cycles

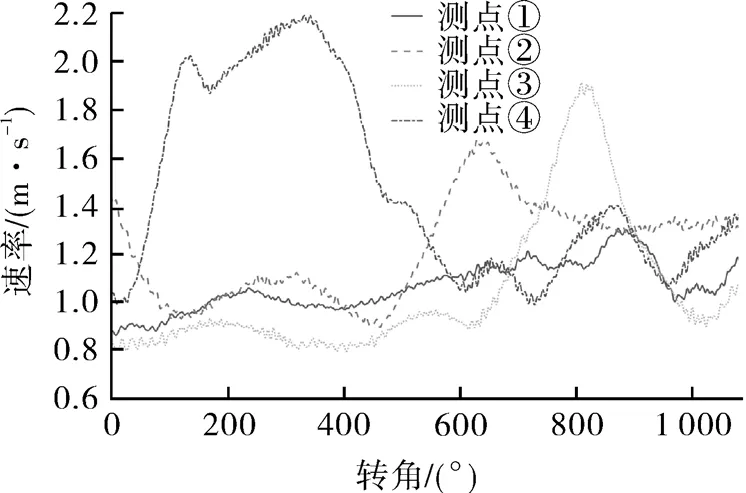
图4 3个周期内电机后腔测点速度幅值变化Fig.4 Velocity fluctuation at measuring points on rear chamber of the motor within 3 cycles

从图可以发现：

（1）压力脉动以旋转频率周期性变化，但速度并不呈现出周期性，且脉动的时间尺度也大于一个周期；

（2）压力脉动整体幅度在160 dB以上，其中在能量集中的频段内幅值也在120 dB以上。而速度的脉动幅度除消声器排气阀膨胀腔及消声器出口外量级小于1 m/s，根据文献［12］提供的估算方法湍流脉动压力在110 dB以下；

（3）腔体内压力等值面的分布与其低阶声学模态表现出一致性，如图5所示。

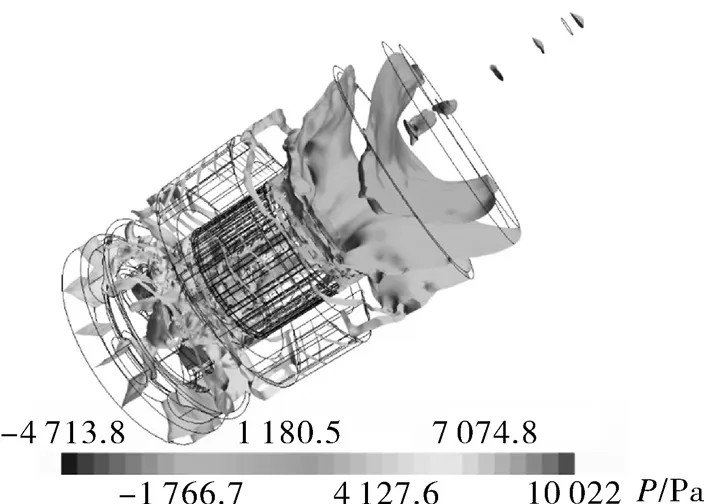
图5 压缩机内部压力等值面Fig.5 Isosurfaces of pressure inside the compressor

湍流产生的压力脉动较声压小10～40 dB，且二者无相关性。电机前、后腔内压力脉动主要是声学响应，在关注频段内表现为峰值皆为工作频率的倍频，而湍流压力频带较宽且频率较低。因此，湍流对压力脉动产生的直接影响可以忽略，主要声源则来自消声器内部。

2.2 压缩机腔内的声压特性分析

采用声学有限元分析压缩机腔内的声压特性，气动噪声源主要在消声器内部，可分为消声器入口（即泵腔出口）质量流入的单极子声源（或活塞面声源）、壁面尤其是挡板和阀座所受流体力的偶极子声源以及挡板涡脱落形成的四极子声源。该压缩机所用消声器为单层四瓣双出口抗性消声器。

通过观察如图6所示计算所得消声器内外涡结构发现从挡板分离出的湍流涡只集中在挡板所在膨胀腔内且涡量较高尺寸较小，一般在6 kHz以上。因此在关注频域内湍流涡不是主要声源，湍流涡产生的压力脉动仅存在于挡板所在膨胀腔内，并不表现出传播性质，如图7所示。由此可以判断在低频段内压缩机内压力脉动系周期脉冲性排气的单极子声响应。为验证该推断，用LMS Virtual.lab对包括和不包括消声器的排气通道分别进行了声学有限元建模和计算，其中消声器入口和出口施加面速度边界条件，其数值由CFD计算结果FFT后所得。

图6 排气时消声器内Q准则等值面Fig.6 Q-criterion isosurfaces in the muffler during exhaust

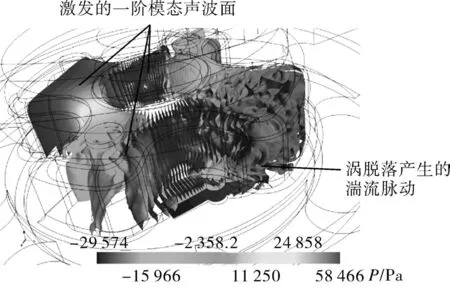
图7 排气时消声器内压力等值面Fig.7 Isosurfaces of pressure inside the muffler during the exhaust

通过选取压缩机顶盖上某点比较声学计算声响应与CFD监测压力变化结果，如图8所示，从图可以发现：（1）CFD计算所得压力脉动在频域不存在110 dB以上非倍频的峰值，说明了宽频噪声的影响在该数值之下。（2）在700 Hz以下频段，二者均与CFD结果吻合较好。该频段满足条件f＜c/2D，其中D为压缩机的高度，即在该频段内为近场声传播。（3）超过上述频率的声学有限元的结果尤其是在声模态频率附近与CFD计算吻合程度较差，但整体趋势基本一致。其中不包括消声器的声学计算在1 600 Hz以上实现了对CFD结果更好的包络。

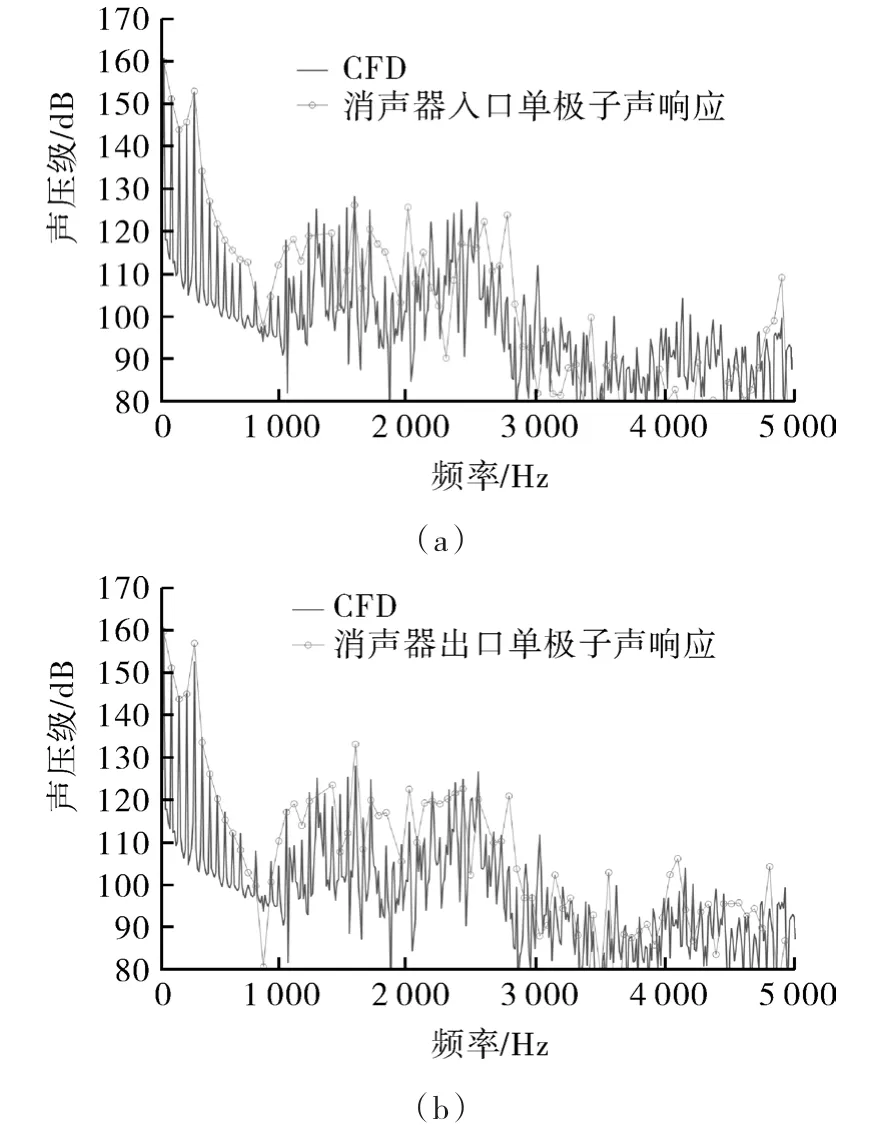
图8 压缩机顶盖压力脉动CFD结果与单极子声响应计算比较Fig.8 Comparison between CFD results of pressure fluctuation of compressor top cover and acoustic FEM under the monopole sound assumption

通过两者比较可以证实消声器之外的排气通道没有显著的声源，说明了泵腔出口的周期性质量注入为导致压缩机内压力脉动的主要声源，在满足近场声传播的低频段内压力脉动完全由其决定。

3 泵腔排气单极子源特性的CFD分析

上述计算中，使用的泵腔出口流量是简化的热力学计算结果，不包含实际几何结构和流动的效应。为更准确分析泵腔出流特性，此处只针对泵腔及消声器区域使用第2节所述方法进行了CFD计算。其中泵腔压缩过程使用动网格方法，忽略阀片运动产生的影响［11-19］。

通过监测泵腔出口的质量流率，可以发现其曲线形状在多个周期内会有变化，并不是严格的周期函数。而在每个周期的排气阶段又存在两大特征，如图9所示。在排气开始的约60°曲轴转角内，质量流率曲线会有幅度较大频率较低的波动，该波动频率与消声器一阶模态的频率相符合；在排气的剩余阶段，会存在幅度较小但频率较高且不断升高的波动，系压力波动在压缩腔内反射产生共鸣的效果。

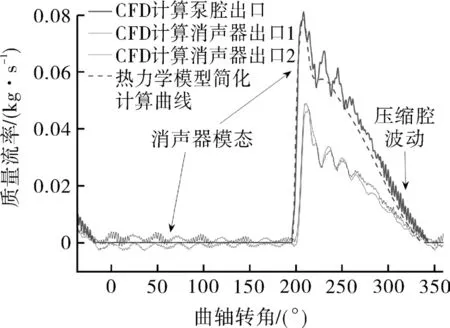
图9 泵腔和消声器出口质量流率Fig.9 Mass flow rate at pump cavity and muffler outlet

通过比较第3节计算采用的基于热力学简化模型所得及该节CFD计算所得的泵腔出口速度的频谱，如图10所示，可以看出消声器可有效降低在其一阶模态频率处的泵腔出口单极子声源强度，而3 500～5 500 Hz频段声源强度有所提高，6 000 Hz以上频段则是压缩腔内压力波动的影响为主。

图10 泵腔出口速度频谱Fig.10 Spectrum of velocity at exit of pump cavity

4 数值分析结果的试验验证

为验证所建立的数值模型，针对计算采用的工况进行了试验测量，在压缩机的排气口放置了动态压力传感器用来记录压力脉动。由于CFD计算在排气出口设置的压力边界条件会使一部分压力波动反射，这里仅将试验测量所得压力脉动的功率谱密度与由第4节所得质量流率进行声学有限元计算结果进行比较，如图11所示。从该频谱中可以看出115 dB以上压力脉动确以工作频率的倍频为主，4 500 Hz以下没有宽频噪声。而在5 820 Hz的峰值则对应了泵腔一阶模态的频率。声学计算结果虽然在数值上与实验结果有一定差异，但其基本趋势符合2 500 Hz以下频段压力脉动系泵腔排气的单极子噪声的判断。

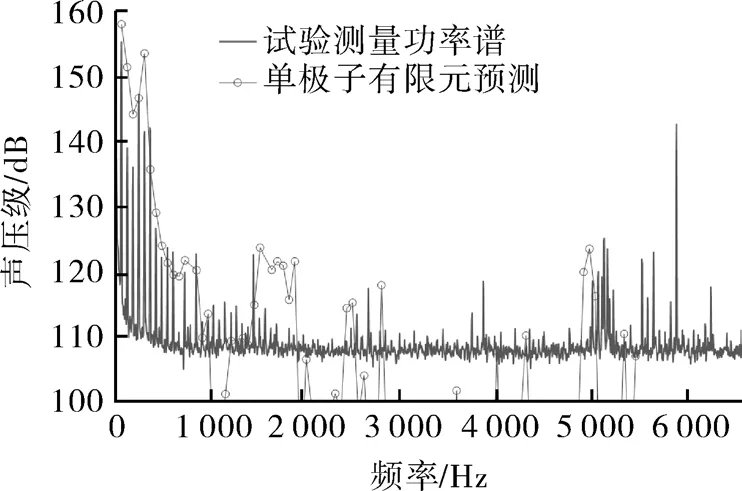
图11 排气压力脉动试验结果与声学计算对比Fig.11 Comparison between the experimental result and acoustic FEM prediction of exhaust pressure pulsation

5 结论

（1）排气过程的压力脉动中声压大过湍流压力约10～40 dB。

（2）声压以泵腔周期性排气的单极子源主导，在满足近场声传播的低频段声学有限元结果与CFD一致。

（3）腔体的声模态对泵腔排气单极子源有影响：消声器可有效降低其消声频率下该声源强度，而压缩腔内波动在高频段是该声源的主要成分。

对于该压缩机而言，湍流噪声不是主要的气动噪声成分，采取措施抑制涡流的产生或促进涡流耗散对降低噪声的作用不大。主要的降噪工作仍需围绕提升排气通道的声传递损失展开。