冲击射流冷却高功率电子元件的试验研究

吕 静，黄伶俐，刘洪芝，吕艈昶

（上海理工大学 环境与建筑学院，上海 200093）

0 引言

21世纪以来，电子设备的发展呈现出微型化、高性能、高集成、高频率的发展趋势，热流密度越来越大，达到100～1 000 W/cm2的高热流密度［1］。电子元件温度过高会危及半导体的结点，损伤电路的连接界面，增加导体的阻值，形成机械应力损伤［2］。研究表明高热流密度电子元件温度每上升 10 ℃，其寿命将减少 50%［3］。

对冲击射流冷却的研究主要集中在结构参数、射流参数和物性参数对换热性能的影响。结构参数主要包括喷嘴直径、喷嘴与壁面间距离、喷嘴与换热面的夹角、换热面的形状、单喷嘴或阵列喷嘴以及是否空间受限等；射流参数主要包括射流出口速度、射流温度等；物性参数主要包括射流介质的密度、黏度、比热等。CHOO等［4］研究了风机的功耗以及射流喷口和风机发热板间的距离对空气冲击射流换热特性的影响。GARIMELLA等［5］对圆形冲击射流进行了试验研究，研究了喷嘴长度与喷嘴直径之比、雷诺数对换热特性的影响。WEN等［6］对圆形喷射管冲击射流进行了试验研究，研究了雷诺数、喷射导管内螺旋线形状、喷口与换热面间距离对换热效果的影响。

国内外的学者将冲击射流冷却与喷雾射流冷却进行了对比研究［7-9］，发现低热流密度下，单相喷雾射流冷却与冲击射流冷却具有相当的冷却效果，而当热流密度较高时需采用多相喷雾射流冷却才能达到与冲击射流相当的冷却效果。GARIMELLA等［10］对浸没式受限冲击射流冷却的流动特性和传热特性进行了试验研究。当换热面积较大时，采用大直径单孔喷嘴进行冲击射流冷却，在热流密度较高时冷却效果不佳且无法覆盖换热面。一些学者提出了阵列冲击射流冷却，可同时满足高射流速度和大覆盖面的要求。FABBRI等［11］采用阵列喷嘴冲击射流冷却电子芯片，芯片热流密度为310 W/cm2，冷却介质温度为23.1 ℃，最终可将芯片温度控制在73.9 ℃。WEATHERS等［12］对多喷结构的高热流密度受限冲击射流进行了试验研究，热流密度高达10 MW/m2，换热系数最高可达到50 kW/（m2·K）。采用阵列喷嘴冲击射流可大大提高整个换热面的换热效率，且壁面温度分布也更加均匀。

冷却技术主要存在两方面的问题：冷却热流密度不能达到要求及冷却不均匀产生热应力。密集冷却和相变冷却是解决以上两个问题的有效手段，相关的冷却技术主要有微通道冷却技术和射流冷却技术。微通道技术虽然有较高的冷却热流密度，但存在压降大的问题。以空气为介质的冲击射流冷却具有散热效率高、结构简单、可靠度高、灵活性强等优点，非常适用于高功率电子设备的散热，在尖端科技中具有很大的应用前景。本文设计搭建一套单束圆形空气冲击射流冷却试验装置，包括射流发生装置、发热元件、数据采集和处理系统，进行空气冲击射流冷却试验，通过改变加热功率、射流温度、喷嘴与壁面间距离和喷嘴直径，得出换热面的温度分布及局部和平均换热系数，并对各因素对电子元件冷却性能的影响进行分析。

1 空气冲击射流理论分析

1.1 空气射流原理

冲击射流是指气体或液体在高压下，通过圆形或狭缝喷嘴垂直或成一定角度喷射到被加热表面，强化对流换热［13］。单个圆形喷嘴冲击射流如图1所示，其主要几何参数有：喷嘴直径、喷嘴与壁面间距离、喷嘴与壁面的夹角（图中所示为90°）、换热面的形状等。冲击射流的流场按流动特性可分为3个特征区域：自由射流区（主射流区），滞止区（驻点区），壁面射流区（贴壁射流区）。自由射流区的流动特性与自由射流相同，下面对滞止区、壁面射流区的换热特性进行分析。

图1 单个圆形喷嘴冲击射流示意Fig.1 Schematic diagram of single round nozzle impinging jet

1.2 空气射流的流动特性

如图1所示，从射流出口到距离壁面Z0的这段为自由射流区，有研究表明，对于圆形冲击射流Z0≈d，d为出口断面直径。流体从半径为R0的喷嘴以初速度u0喷出，出口断面上的流速视为均匀分布。沿着射流方向，由于卷吸作用将周围物质不断带入到射流流场中，使得流量沿程增加，射流断面不断扩大且射流主体的速度逐渐降低，湍流度增强。如图1中所示锥形体部分，该区域速度等于出口速度u0，称为射流核心区（或势流核心区），其余部分速度小于u0，称为边界层。边界层随射程的增大同时向外和向内扩散，直到扩散至射流轴心线处，此时核心区消失，只有轴心点上的速度为u0，这一断面称为过渡断面（或转折断面）。从射流出口至过渡断面为射流起始段，起始段射流轴心线上的速度一直为u0。过渡断面后称为射流主体段（或基本段），主体段轴心速度沿射流方向不断降低，直至为0，主体段完全被边界层占据。

1.2.1 射流运动特征

射流的运动特性是其各横截面上的速度分布具有相似性，射流各横截面上的无因次速度分布可用半经验公式表示为：

式中 u——y点上的速度，m/s；

um——截面轴心速度，m/s；

y—— 横截面上任意一点至轴心线的距离，m；

R——截面上的射流半径，m。

由此可得出y/R从轴心或核心区边界到射流外边界的变化范围为0→1；u/um从轴心或核心区边界到射流外边界的变化范围为1→0。

1.2.2 射流运动分析

（1）轴心速度。

式中 u0——出口速度，m/s；

Qw—— 紊流系数，本文中采用圆形喷射，aw=0.08；

R0——出口圆断面半径，m。

（2）起始段核心长度Sr。

当 um=u0，S=Sr时有：

式（2）说明无因次轴心速度与无因次距离成反比，即主体段轴心速度随射流距离的增大而减小。式（4）说明核心长度与出口断面半径R0成正比，出口断面半径越大，核心区就越长。若喷嘴与壁面间距离H＜Sr，即换热面处于核心区内，此时虽然断面平均流速随射流距离的增大而减小，但相差不大，射流湍流度随H的增大而增大，湍流度增大促进换热，理论上换热效果应增强，并在H=Sr时达到最大。喷嘴与壁面间距离H继续增大，当H＞Sr时，随H的增大，射流速度明显减小，湍流度增大，此时若湍流度促进作用大于速度的削弱作用，则换热效果增强，若速度的削弱作用大于湍流度的促进作用时，换热效果减弱。

1.3 空气射流的传热特性

1.3.1 驻点区

滞止区又称驻点区，在这一区域，流动速度迅速滞止为0，射流方向由轴向转为径向，产生很高的压力梯度，使得滞止区的参数变化最为剧烈，局部换热强度非常高，这也是冲击射流相较于平行剪切射流的优势所在。热边界层内，温度分布可用四次多项式近似表达［14］：

式中 Pr——普朗特数；

Z——射流口到壁面距离，m；

Δ——温度边界层厚度，m；

h——对流换热系数，W/（m2·K）；

d——喷嘴的直径，m；

λ——导热系数，W/（m·K）。

1.3.2 壁面射流区

壁面射流区又称贴壁射流区，在滞止区压力梯度的作用下，流体贴壁面向外流出，在该区压力逐渐恢复为静压，流动逐渐接近于平行壁面［15］。壁面射流区的努塞尔表达式［14］为：

式中 r ——滞止点为圆心的圆的半径，m。

由式（1）（2）可得：影响冲击射流冷却效果的因素主要包括喷嘴直径、喷嘴的出口高度、换热面的形状、射流介质、射流出口速度、射流温度等。

2 试验系统

2.1 试验台

以空气、单束、圆形喷嘴、紊流射流为重点，设计搭建了一套冲击射流冷却试验系统。由于采用空气为冷却介质，无需回收，故设计为更加安全稳定的开式系统，主要包括空气处理系统、模拟加热系统、数据采集和处理系统，其基本流程如图2所示。空气处理系统为上海理工大学焓差室，可将空气处理至试验所需状态；空气由焓差室处理后进入空气压缩机，通过调节空压机转速和阀门开度可控制空气出口流量；发热元件采用加热棒加热紫铜块，由变压交流电供电，通过调节输入电压可控制热源表面热流密度；喷口与加热表面的距离可通过升降支架调节。主要测量采集的参数有气体流量、射流空气温度、加热表面温度等，试验数据由数据采集仪采集并由计算机输出。射流送风管道采用直径为20 mm的不锈钢圆形管道。

图2 冲击冷却试验系统基本流程Fig.2 Flow chart of shock cooling experiment system

2.2 试验部件及仪器

2.2.1 试验仪器

试验采用空压机为试验系统提供所需压力，系统配备一台小型空压机。根据喷头最大流量为138.5 L/min，并选择合适的气体质量流量计。试验选用圆柱形喷嘴，其直径分别为1.2，1.4，1.6，1.8，2.0，2.2 mm。选择一台可控硅电子调压器，换热表面温度采用 Agilent34970A与计算机连接采集数据，软件采用Agilent自带的 Benchlink Data Logger II，所得数据用Excel 表格输出。各仪器的相关参数见表1。

表1 仪器参数Tab.1 Instrument parameter table

2.2.2 电子元件及测点布置

试验采用热棒加热紫铜块作为发热元件，选用3根加热功率为90 W的加热棒，理论最大热流密度为175.3 W/cm2；采用紫铜块作为导热体，导热体由基座和颈部两部分组成，导热体颈部设计直径为14 mm，长20 mm，3根加热棒间呈120°均匀布置在导热体基座中。测点温度由自制的直径为0.5 mm的T型热电偶测量。由于无法直接在换热表面布置热电偶测其温度分布，故在导热体颈部距换热面2 mm处布置6个热电偶，相邻热电偶间呈60°，由于温度分布对称，因此6个测点布置如图3所示。

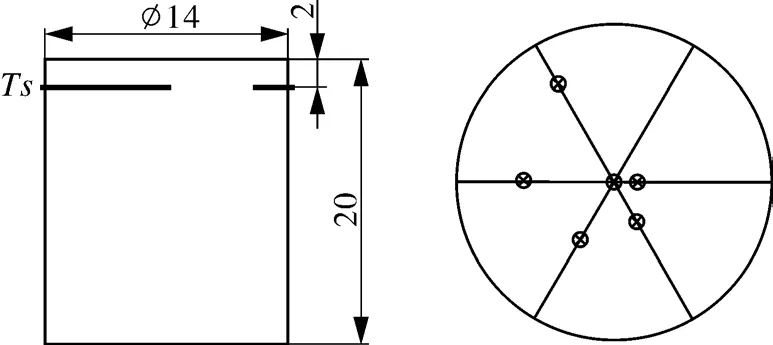
图3 温度测点布置Fig3 Layout of temperature measuring points

3 试验结果与分析

通过改变加热功率p、射流温度T、喷嘴与壁面间距离H和喷嘴直径d（定流量），气体流量都为75 L/min，得到24组工况见表2，试验测量见表中的24个工况，每种工况下测量的试验数据为3次测量值的平均数，计算得到各工况下壁面温度的分布、壁面局部换热系数和平均换热系数，分析以上4个因素对射流冲击换热效果的影响。

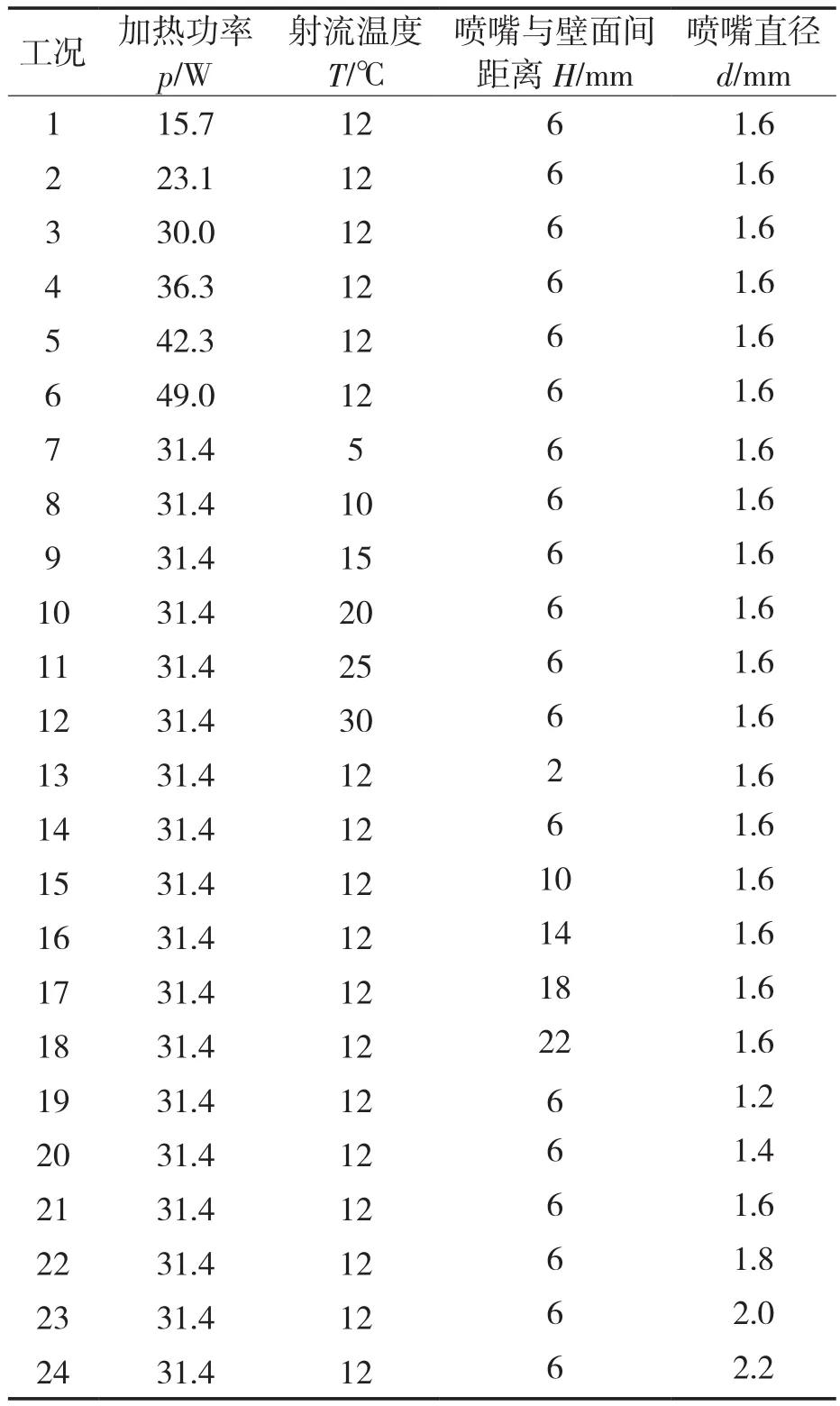
表2 试验工况Tab.2 Experimental conditions

3.1 加热功率的影响

在不同加热功率的工况下，对应的换热面实际热流密度为 9.13，13.47，17.44，21.10，24.58，28.46 W/cm2，换热面各测点的温度见表3。在不同加热功率下，壁面温度最低点的位置均在r=2 mm处，最高点的位置均在r=5 mm处。随着加热功率的增大，壁面平均温度近似线性增长，相对增长率约为2.89%，说明当电子元件的发热功率很高时，若不采取更有效的冷却措施，元件温度将快速升高。不均匀度随着加热功率的增大而增大，即换热面温度分布越不均匀。

表3 不同加热功率工况下各测点温度Tab.3 Measuring point temperature under different heating power conditions

由图4可以看出，不同加热功率时局部换热系数分布曲线几乎是重合的，即局部换热系数的大小和径向分布基本不随加热功率发生变化。r=2 mm处的局部换热系数最大，r=5 mm处的局部换热系数最小。不同加热功率时的平均换热系数的变化不大，最大值与最小值相差26.27 W/m2·K，几乎不变，因此加热功率对冲击射流换热系数几乎没有影响。

图4 不同加热功率时的换热系数Fig.4 Measuring point temperature of different heating power

3.2 射流温度的影响

在不同射流温度工况下，对应换热面实际热流 密 度 分 别 为 18.38，18.26，18.14，18.02，17.91，17.78 W/cm2，换热面各测点的温度如表4所示。在不同射流温度下，壁面温度最低点的位置均在r =2 mm处，最高点的位置均在r=5 mm处。壁面平均温度随着射流温度的增大而增长，相对增长率0.91%，升高幅度较小。不均匀度随着射流温度的升高而减小，即射流温度越高，壁面温度分布越均匀。

由图5可以看出，不同射流温度时局部换热系数最大值均位于r=2 mm处，最小值均位于r=5 mm处。可以发现，改变加热功率和射流温度，局部换热系数沿径向的分布规律始终不变，因为局部换热系数的径向分布主要取决于壁面上速度和湍流度的分布，而加热功率和射流温度的改变均不会对速度和湍流度产生影响。平均换热系数随着射流温度的升高而增大，但增大幅度较小，相对增长率仅0.14%。射流温度升高导致换热效果略有提高是由于空气物性参数随空气温度升高而有所变化，但影响作用不大。

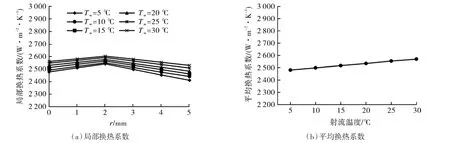
图5 不同射流温度时的换热系数Fig.5 Heat transfer coefficient of different jet temperature

3.3 喷嘴与壁面间距离的影响

在不同喷嘴与壁面距离工况下，对应的换热面实际热流密度为 18.10，18.07，17.91，17.70，17.46，17.20 W/cm2，换热面各测点的温度如表5所示。壁面温度呈现出两种不同的分布情况。距离H为2,6 mm时，在r=2 mm处温度达到最低，在r=5 mm处达到最高，两者温差随距离增大而增大；在其他的距离，温度在驻点（r=0）处达到最低，在r=5 mm处达到最高，两者温差随距离的增大而减小。壁面平均温度随距离的增大而升高，距离由2 mm增大到6 mm时，平均温度的相对增长率为0.27%，温升幅度很小；而距离由6 mm增大到22 mm时，平均温度的相对增长率为1.80%，温度幅度较大。不均匀度随着距离的增大，先增大后减小，H=10 mm时温度分布最不均匀。

表5 不同喷嘴与壁面间距离时各测点温度Tab.5 Measuring point temperature of different distance between nozzle and wall

由图6可以看出，距离H为2，6 mm时，r=2 mm处的局部换热系数最大，r=5 mm处最小，两者的差值随距离增大而增大；其他的局部换热系数分布相同，驻点处的局部换热系数最大，沿径向减小，换热系数最大值与最小值的差值随距离增大而减小。可以发现，当距离增大时，局部换热系数最大值的位置发生移动，这是因为距离的变化引起了壁面上速度和湍流度的变化。平均换热系数随着距离的增大而减小，间距离由2 mm增大到6 mm时，平均换热系数下降不明显，相对增长率为-0.35%。而当距离大于6 mm时，平均换热系数明显减小，相对增长率为-2.34%。计算喷嘴直径为1.6 mm时射流的核心长度［16］为：Sr=6.71 mm。因此，距离分别为2和6 mm时，换热面所处位置在核心区以内，而在其他距离时，换热面所处位置在核心区以外，这就导致距离H分别为2，6 mm时换热面的换热特性较为接近。

图6 不同喷嘴与壁面间距离时的换热系数Fig.6 Heat transfer coefficient of different distance between nozzle and wall

3.4 喷嘴直径的影响（定流量）

在不同喷嘴直径工况下，对应的换热面实际热流密度为 18.70，18.46，18.13，17.78，17.44，17.05 W/cm2，换热面各测点的温度见表6。壁面温度沿径向均先降低后升高，均在r=5 mm处的壁面温度最高，但温度最低点位置有所不同。直径d为1.2，1.4 mm时，r=1 mm处的壁面温度最低；在其他直径时，r=2 mm处的壁面温度最低。壁面平均温度随直径增大而增大，相对增长率约为59.80%，说明在不改变射流流量的情况下，略微增大喷嘴直径就会导致壁面温度急剧升高。不均匀度随着直径的增大而减小，即随着喷嘴直径的增大，换热面温度分布越均匀。

表6 不同喷嘴直径时各测点温度Tab.6 Measuring point temperature of different nozzle diameter

由图7可以看出，当直径为1.2 mm和1.4 mm时，r=1 mm处的局部换热系数最大，r=5 mm处最小；在其他直径为时，r=2 mm处的局部换热系数最大，r=5 mm处最小。射流流量不变时，随着直径的增大，局部换热系数最大值的位置有外移的趋势，差值减小，换热越均匀。随着直径的增大，各测点的局部换热系数均减小，减小程度降低。射流流量不变时，平均换热系数随着喷嘴直径的增大而减小，当喷嘴直径增大到1.8 mm时，减小趋势减缓。

图7 不同喷嘴直径时换热面局部和平均换热系数Fig.7 Local and average heat transfer coefficients of different nozzle diameters

4 结论

（1）加热功率在15.7～49.0 W范围内，沿径向壁面温度均先降后升、换热系数先增后减；随着加热功率增大，壁面径向温度分布越不均匀、平均温度升高，加热功率对换热系数没有影响，最大换热系数的位置不变。

（2）射流温度一定，沿径向壁面温度先降后升、换热系数先增后减；随着射流温度从5℃升高到30℃，壁面平均温度小幅升高、径向温度分布越均匀，空气物性发生变化，换热系数略有提高，但换热系数的最大值位置不变。

（3）通过以上研究得出，径向温度和局部换热系数的分布规律主要受壁面上速度和湍流度的影响，而这又取决于射流到达壁面时的速度和湍流度。改变加热功率和射流温度对速度和湍流度均没有影响，因此温度最小值和换热系数最大值的位置始终不变。