精密单波束测深分析与实践
郭志金 何雯 罗晔


摘要:随着对多波束系统组成单元的研究不断深入,多传感器集成技术已从传统单波束测深向精细化方向发展。在分析普通单波束测深精度因子的基础上,重点针对延时效应、动吃水效应和波束角效应进行了分析和试验。试验结果表明:对于中高速运行的测船测深作业,应进行延时改正;采用波束角小的换能器以无验潮模式进行单波束测深可有效提高测深精度。得出了测深传感器实时姿态对测深精度的影响,以及水下不同地貌对测深传感器的敏感性。
关键词:精密测深;单波束;精度因子;地貌敏感性
中图法分类号:P332 文献标志码:A DOI:10.15974/j.cnki.slsdkb.2021.05.005
文章编号:1006 - 0081(2021)05 - 0019 - 04
影响水深测量精度的因素很多,如定位误差、验潮误差、动吃水误差、声速误差、测船姿态变化导致的误差等。以往的研究证实:采用RTK三维水深测量的无验潮模式测深能有效解决定位、验潮和动吃水误差[1],同时声速剖面改正能有效减弱声速效应引起的测深误差。但实际工作中,也不能只追求测深精度而大量搭载各种传感器,应依据地形特征分析各传感器对测深精度提升的贡献率,然后选择搭载。应在分析普通单波束测深精度因子的基础上,重点针对延时效应、动吃水效应和波束角效应进行分析和试验,选择最优的测深传感器组合。
1 精密测深主要精度因子
不同于普通测深,分析了影响精密单波束测深精度的因素,并对采集到的数据处理进行优化。单波束测深精度的主要影响因子如下[2-4]。
1.1 延时效应和动吃水效应
测深系统性延时包括测深数据延时、定位数据延迟、采集软件处理时间及定位和测深单元安装偏差[5-6]。延时效应导致岸坡等区域等高线呈现锯齿状,与实际平顺的岸坡地形特征严重不符。一般采用如下3种方案减弱延时效应:①降低船速,以减小延时导致的定位点和测深点位置偏差。②测前先验算时延值,然后开始作业,选取坡比较大区域进行往返测,调整时延值达到往返断面的最佳吻合。③通过后处理软件对原始数据进行延时补偿。
动吃水效應主要表现为起伏水流导致的船体垂荡,以及测船行进速度变化时船体吃水的变化。采用无验潮测深模式时,垂荡值已在GNSS高程信息中体现[7-8],可不用考虑;采用验潮测深模式时,宜加装涌浪传感器,以改正测深值[9-10]。
1.2 波束角效应
由于传播过程中能量的衰减,测深换能器发射的波束中,只有一定开角内的回波才能被换能器接收。根据底跟踪原理,换能器只记录此开角范围内最早的回波作为计算水深的依据,因此水深值可能是开角范围内水底任意点至换能器的距离,即波束角效应。以下从不同地形角度分析波束角效应对测深精度的影响。
(1)坡向不变区域。如图1所示,在波束角效应影响下,实测水深并非测船定位点正下方水深,河底地形坡度的存在导致地形测量值失真,总体上表现为坡面向坡脚方向平移。
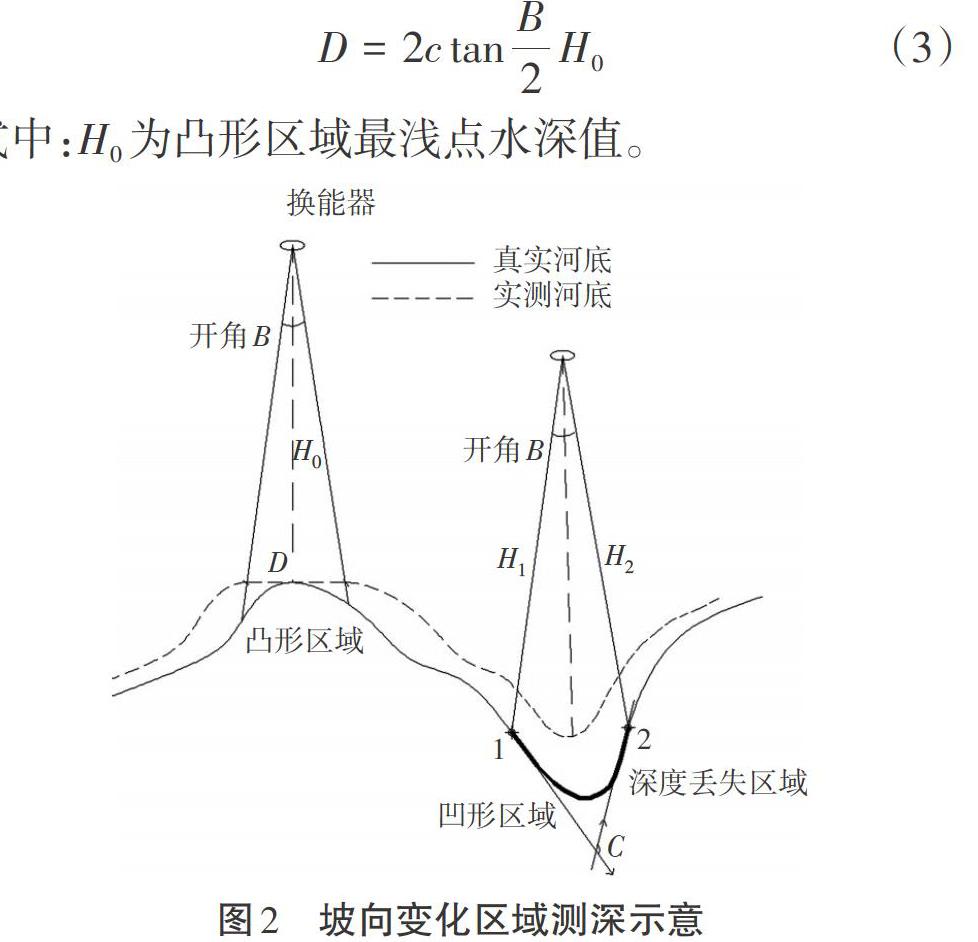
(2)坡向变化区域。如图2所示,对于凸形水底,波束角效应在一定区域内表现为顶部加宽变平,两侧在坡向不变区域表现为平移。顶部平滩宽度为
对于凹形水底,测船前进过程中,当出现波束脚印范围内非平坦地形但边缘波束水深[H1=H2]时,必然导致凹槽底部黑色区域部分水底数据丢失。由图2可知,只有当凹槽底部平缓,点1和点2切线对应夹角C小于开角B时,凹槽最低点深度不会丢失。
综上所述,波束角效应带来的测深误差与波束角和水深成正比,随地形起伏程度的加剧而增大。波束角效应的关键在于波束脚印大小,因此在进行水下地形施测时,宜先调查测区水深范围,根据测图比例尺测点间距要求和脚印大小选择合适开角的换能器。
1.3 姿态效应
在测深作业中,受风浪等影响,测船颠簸造成换能器无法保持垂直向下,必然有横摇α和纵摇β,导致定位点和波束脚印平面位置不重合,需要进行平面坐标改算和深度改正。
(1)平面坐标改算。首先以GPS相位中心为原点,船体前进方向为x轴建立船体的左手坐标系,波束脚印的船体坐标系平面坐标为
(2)深度改正。
2 试验与分析
2.1 试验组织实施
试验选择在长江中游河段进行,水深区间为(4 m,45 m),坡度区间为(0°,35°),分别采用单波束测深系统配合8°开角和3°开角的换能器,以无验潮模式采集水下地形。试验对姿态效应的影响只作定性分析,分别采用两条航行稳定性不同的测船(水文021测船和快艇)施测。每组数据包含6条测线,测线间隔为15 m,测点间距为2 m。同时采用波束角为1°×0.5°(航向×垂向)的多波束测深系统进行水下地形精细化扫测,以此作为参考值对比分析单波束测深精度的影响因素。
2.2 成果对比分析
(1)动吃水和延时效应分析。采用快艇测深时,行进中船尾下沉明显,解算快艇行进时的实时潮位,并与验潮模式潮位比较,结果见图3。可见快艇测深时,动吃水因素对测深质量影响极其明显,为提高测深精度必须采用无验潮模式。分别基于未进行延时改正和已进行延时改正的测深数据作图,见图4。由图4可见,成图比例尺越大,等高线锯齿表现越明显,进行改正后,效果明显。
(2)波束角效应和姿态效应分析。分别以多波束系统和3°,8°开角单波束系统获取的数据绘制河道横断面图,并作叠合分析,见图5。由图5可见,单波束实测地形在斜坡区域有明显的平移效应,平移值大小随波束角和深度的增大而增大。在平坦区域无明显差异,但依然总体高程较多波束测点高程低。
计算河道过水断面面积比例误差和28 m水位时的槽蓄量[9]比例误差,见表1。由表1可知,随波束角的减小,过水面积和槽蓄量计算精度明显提高。同时,姿态稳定的作业平台对精度提升有一定的贡献率。
分别以4种作业形态的单波束测深数据和多波束點云数据为数据源,应用克里金插值法,建立曲面模型。对两曲面模型进行栅格代数求差运算,以此研究误差大小及其分布特征,统计结果见表2。
为直观研究误差分布特性,将求差之后的DEM贴合于三维模型上,以波束角8°和多波束数据为例,见图6。由图6可见,斜坡区域整体高程精度偏低,且随深度的增加误差逐步增大,同深度坡度越大精度越低;平坦和浅水区域整体精度较高。可将测区分为浅水平坦区(水深H≤15 m、坡度A≤5°)、深水平坦区(H>15 m、A≤5°)、缓坡区(5°
表3精度分区统计结果表明,在平坦区域,测深对定位精度因素不敏感,姿态效应与波束角效应对测深精度影响较小。在陡坡区域,姿态效应与波束角效应对测深精度影响较为显著。
3 结 语
本文分析了单波束测深的主要精度因子,并通过实测数据分析可知,在单波束水深测量中,地形的复杂程度和波束角的大小是影响测量精度的显著因素。通过算法改进可减少延时、姿态等因素的影响。然而本文试验未能集成姿态数据对定位和测深数据进行精细化修正,应在以后的研究中加以改进和完善。
参考文献:
[1] 王真祥. 多传感器集成下的精密无验潮水深测量方法研究[J]. 人民长江, 2019, 50(12):60-65.
[2] 刘雁春, 陈永奇. 海道测量定位与测深的延时效应[J]. 海洋测绘, 1999(1):27-34.
[3] 郭发滨, 申宏, 雷宁,等. 水声换能器动态吃水与传感器技术探讨[J]. 海洋测绘, 2005, 25(5):25-27.
[4] 刘雁春, 陈永奇. 海洋测深的波束角效应及其改正[C]// 北京:海洋测绘综合性学术研讨会,1998:22-29.
[5] 彭刚跃, 郭珍珍.无验潮模式水下地形测量的水位改正方法[J].北京测绘,2019(4):472-475.
[6] 丁继胜, 刘忠臣, 周兴华,等. 利用姿态传感器提高单波束测深精度[C]// 第十四届海洋测绘综合性学术研讨会. 北京:中国测绘学会, 2002.
[7] 赵建虎. 现代海洋测绘[M].武汉:武汉大学出版社,2008.
[8] 李东峰, 韩磊. 潮位仪与GPS测定水面高程的方法研究及应用[J]. 测绘与空间地理信息, 2020, 43(5):155-157.
[9] 水利部水文局.水道观测规范:SL257-2017[S].北京:中国水利水电出版社,2017.
[10] 李俊晓, 李朝奎, 殷智慧. 基于ArcGIS的克里金插值方法及其应用[J]. 测绘通报, 2013(9):87-90.
(编辑:李 慧)
Abstract:With the increasingly intensive research on the components of multi-beam system, the technology of multi-sensor integration has become the fine sounding development direction of traditional single beam bathymetry. Based on the analysis of the influential factors of precision of common single beam sounding, the analysis and test of delay effect, dynamic draft effect and beam angle effect were focused. The results showed that the delay should be corrected for the sounding operation at medium and high ship speed, and the single beam sounding with smaller beam angle transducer in non tidal mode can effectively improve the sounding precision. The influence of the real-time attitude of the sounding sensor on the sounding precision was described. The sensitivity of different underwater landforms to the sounding sensor was compared and analyzed.
Key words:precise sounding;single beam;precision factor;geomorphological sensitivity

