难以分清的“葡萄”和“葡萄干”
周游

[摘 要]引导学生解难题时,教师不能局限于一种方法,而应该根据学生学习的基础和知识的更新情况,适时调整方法,改换策略,从列表策略过渡到“比例”的方法,提高解题效率。
[关键词]列表;对应关系;比例
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)20-0045-02
偶然读到一篇数学论文,题目为《从“晒制葡萄干”说起》,文中提到一道经典的数学应用题“用4千克的葡萄可以晒制葡萄干1.6千克,照这样计算,1千克的葡萄可以晒制葡萄干多少千克?要晒制1千克葡萄干需要多少千克葡萄?”,并提供了两种解题方法。第一种:锁定问题,即最后求的是葡萄干还是葡萄的质量。如果求的是葡萄干的质量,那就用葡萄干的质量除以葡萄的质量;如果求的是葡萄的质量,那就用葡萄的质量除以葡萄干的质量。第二种:锁定问题的开头语。如果问题的开头语是1千克葡萄,那就把葡萄的质量作为除数,葡萄干的质量作为被除数,列一个除法算式;如果问题的开头语是1千克葡萄干,那么就倒过来,把葡萄干的质量作为除数,葡萄的质量作为被除数,列一个除法算式。显然,一些教师认为与其费尽唇舌还不能让学生领悟个中原委,不如直接用断句法和语句推敲法“快刀斩乱麻”,但这种做法是极其短视的。
一、词句分析法不可取
五年级的学生开始学习小数和分数,习题及测试卷中常常会出现“黄金搭档”填空题,如“火神山建筑队每1.5小时可以粉刷120平方米的外墙,照这样计算,火神山建筑队1小时可以粉刷( )平方米的外墙?粉刷1平方米外墙要( )小时?”,对于此类题,学生的答题正确率比较高,但对于变式题“用4千克的葡萄可以晒制葡萄干1.6千克,照这样计算,1千克的葡萄可以晒制葡萄干多少千克?要晒制1千克葡萄干需要多少千克葡萄?”,学生的答题正确率则呈断崖式下降。
笔者访谈了不少学生,以了解其中原因。其一:前一题有相应的数量关系式“施工速度=任务量÷施工时间”“施工时间=工程总量÷施工速度”,而后一题则缺少这种通识性的数量关系式作为支撑。其二:前一题中,当目标量的单位是“平方米”时,就用120平方米除以1.5小时;当目标量的单位是“小时”时,就用1.5小时除以120平方米。因为根据除法性质,商的单位和被除数的单位要保持一致,因此商和被除数应是同类量,而后一题中所有的单位都是千克,就难以据此列式了。
二、列表找对应关系
由以上分析可见,教学中不应只关注学生做题结果的正确率,还应关注学生的思考过程,在学生理解的基础上建立除法解题模型,让学生在解决问题的过程中积累基本的数学经验。
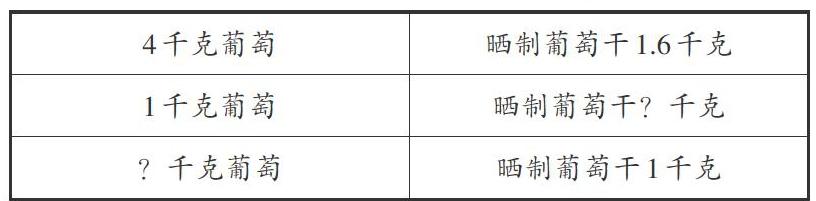
为此,笔者总结出了“回环相除”题型,即不论哪一个量除以哪一个量,都是围绕着一个基本的数量关系式“总数÷份数=每份数”来展开的。当然,这必须具体情况具体讨论,因为“总数”和“份数”会随着题意的变化而进行“角色互换”。因此,教师首先要指导学生反复读题,明确“总数”和“份数”分别对应的量,对于不便明确的量,推荐使用列表法。首先,用列表摘选条件的方法来解析题意。列表过程虽然琐碎,但是对精准分析题意发挥着重要的作用。经过一段时间的练习,学生就可以做到在脑海中形成虚拟表格,并成为一种下意识的行为。其次,要重视列表摘选条件的方法指导。虽然,学生在四年级学过列表法,但对列表法的运用还是很生涩,此时教师的指导很关键。第三,列表后的对比辨析至关重要。如下表:
分析表中数据可以发现,葡萄和葡萄干的质量是有对应关系的,葡萄质量增加,葡萄干的质量也相应增加,葡萄的质量减少,葡萄干的质量也相应减少。既然存在这样的对应关系,就可据此进行具体分析,如表格中4千克葡萄→1千克葡萄,缩小了4倍,那么晒制的葡萄干的量也相应缩小4倍,变为1.6÷4=0.4(千克);当葡萄干1.6千克→葡萄干1千克时,缩小了1.6倍,那么葡萄的量也相应缩小1.6倍,变为4÷1.6=2.5(千克)。利用列表法,可帮助学生看清葡萄和葡萄干之间的一一对应关系,为解题提供了思路。由此可见,列表分析对应关系比先计算每份数更符合学生的思维特性。
三、从比例的角度来理解
到了六年级,学生学了比例知识后,“晒制葡萄干”的解决途径又多出一条。在列表分析对应关系的基础上,让学生进一步理解“同样的葡萄作原料,葡萄干的出产率是一定的”“相对应的葡萄干与葡萄(或者葡萄与葡萄干)的比值是一定的”“相对应的葡萄干与葡萄(或者葡萄与葡萄干)存在比例关系”。学生很快发现:4千克葡萄∶1.6千克葡萄干=1千克葡萄∶?千克葡萄干,可列出比例式4∶1.6=1∶x,反过来1.6千克葡萄干∶4千克葡萄=?千克葡萄干∶1千克葡萄,可列出比例式1.6∶4=x∶1;4千克葡萄∶1.6千克葡萄干=?千克葡萄∶1千克葡萄干,可列出比例式4∶1.6=y∶1,反过来,1.6千克葡萄干∶4千克葡萄=1千克葡萄干∶?千克葡萄,可列出比例式1.6∶4=1∶y。这时,列比例式的方法比列表找对应关系方便得多。
“列比例式”的方法,可有效解决“已知巨峰葡萄晒制葡萄干的出产率为40%,50千克巨峰葡萄可晒制多少千克葡萄干?要晒制50千克葡萄干需要多少千克巨峰葡萄?”这一问题。学生只要理解“出葡萄干率=葡萄干的千克数÷葡萄的千克数”,便能顺利地列出“x/50=40%”“50/y=40%”。类似的求治愈率、到岗率等的问题也都可以迎刃而解。当然,在更复杂的分数应用题中,该方法也能够大显神威。如“方舱医院新冠肺炎男性、女性患者的比是4∶3,转走2名女患者后,男性和女性女患者的比是6∶5,求原來男性、女性患者各有多少人?”这样一道题,以往的解法是,先设“男性患者人数”这个不变量为单位“1”,求出原来女性患者人数占单位“1”的3/4,后来女性患者人数占单位“1”的5/6,再用2÷(5/6 -3/4)=24求出男性患者人数,最后求出原来的女性患者人数。现在,可以根据比例列出方程:[4x/3x-2=65]。在后面的拓展题“方舱医院收治的新冠肺炎男性、女性患者人数的比是4∶3,转走2名男性患者,又转进1名女性患者后,男性、女性患者的比是6∶5,求原来男性、女性患者各有多少人?”中,关系较为复杂,但学生可以利用比例列出方程:[4x-23x+1=65]。
一道看似寻常的“晒制葡萄干”题,引出不同的解题方法。教师应该时刻保持科研者的心态,敏锐地嗅出数学题背后的知识链接,引导学生寻求问题的破解之道。
(责编 罗 艳)

