关于圆的有关内容教材编写及二次开发研究（三）

刘慧

[摘 要]针对研究（二）中分析的教材编写圆的面积探究活动存在的问题，提出了对教材中圆的面积进行二次开发的思路以及修改课程标准的建议，并结合教学实践证明其可行性;给出了估计、猜测圆的面积之探究活动设计的建議，简单介绍二次开发思路中蕴含的数学思想方法。

[关键词]圆;面积;教材;二次开发

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）20-0008-03

《关于圆的有关内容教材编写及二次开发研究（二）》中分析探讨了圆的面积的“画—分—剪—拼”方法存在的诸多问题，说明了其不可行性。为了解决《关于圆的有关内容教材编写及二次开发研究（二）》中提出的问题，也为了使学生更好地学习圆的面积，下面将提出对教材进行二次开发的建议并进行说明。

一、二次开发的建议

第一，编排圆的基本知识（圆心、半径、直径），以及圆的周长和其求法公式（含圆周率）。

第二，编排扇形的基本知识（顶点、圆心角、弧、弧长），及用弧长和半径表示的扇形面积公式。

第三，编排圆的面积。关于圆的面积，可以先用方格纸或圆内接与外切正方（多边）形进行估计，提出猜想;再用扇形面积公式推导圆的面积公式。当然，也可以不进行估计，直接转化为用扇形面积公式推导圆的面积公式。

二、二次开发的建议说明

1.需解决的问题——修改课程标准有关内容

数学课程标准在“第二学段（4～6年级）”中关于扇形的有关内容：“5.通过观察、操作，认识平行四边形、梯形和圆，知道扇形，会用圆规画圆。”这里也就是让学生认识扇形这个图形，及其定义和构成元素——顶点、圆心角、弧。而弧长的概念及求法，以及扇形的面积公式的内容出现在数学课程标准第三学段（7～9年级）“（7）会计算圆的弧长、扇形的面积”。可见，上述设计思路要得到落实，就有必要对课程标准进行修改。这也是浙教版和冀教版教材在推导圆的面积公式时，使用扇形面积公式，而没有明确指出的原因，因其超越了第二学段的课程标准要求。因此要使上述设计思路得以实施，建议课程标准在第二学段（4～6年级）的有关内容做如下修改。

（1）在“二、图形与几何”中，将“（一）图形的认识”部分之“5.通过观察、操作，认识……圆，知道扇形……”（第12页）中的“知道扇形”改为“简单认识扇形”，意在增加“弧长”的概念。

（2）在“（二）测量”之“4.通过操作，了解圆的……解决简单的实际问题。”后，添加“会计算一些圆心角为特殊角的扇形的弧长，掌握用弧长和半径求扇形面积的公式，并能解决简单的实际问题”。

这样一来，设计思路中的第二条就可以符合课程标准的形式正大光明地出现了。前述浙教版和冀教版教材出现的“犹抱琵琶半遮面”“羞羞答答”的尴尬局面也可打破，为第三条“根据扇形面积公式推导圆的面积公式”铺平了道路，可大大减少机械式的拼图等不必要的麻烦。

2.修改课程标准有关内容的其他原因分析

首先，现行教材除北师大版教材只是出现扇形名称外，其他教材都给出了扇形的定义及有关概念，且都（含北师大版教材）配备了一些计算特殊扇形周长和面积的练习题。如，浙教版教材第75页（如图1）、76页（如图2）有不少与扇形面积有关的问题;苏教版教材第101页（如图3）的第14题和思考题都是求扇形面积的练习题;等等。苏教版、冀教版、西师大版、青岛版教材均把扇形内容的编排放在了圆的面积之前。故先学习扇形及其面积公式是有必要的。

其次，各教材在利用“画—分—剪—拼”探究方法把圆转化为已学过的图形时，将圆形纸片等分后，青岛版和北师大版教材就直接给出分成的小扇形，人教版教材则是分成近似的等腰三角形。这种情况下，就是不讲扇形面积公式，而用三角形面积公式近似推导圆的面积公式，误差更小，近似程度更高，学生也更好理解。而用分成的众多小扇形拼成图形，再将曲线取直转化成平行四边形、长方形等学生已学过的图形，误差大不说，还说是圆的面积公式，学生能信服？既然如此，何必先近似得出圆的面积公式，而后到初中再由圆的面积公式推导出扇形面积公式呢？

最后，先学习用半径和弧长表示的扇形面积公式，学生好懂好理解。这是因为，当扇形的圆心角比较小时，扇形就和三角形很相似或接近，此时渗透类比方法，引导学生猜想扇形面积公式就很容易。按青岛版教材的编排，在学生学习了扇形的有关知识后介绍弧长，然后给出一个圆心角比较小的扇形的弧长和半径的长度，让学生求其面积，结果在没有任何提示的情况下，两个班共90人中，有86人（占总人数的95.56%）用三角形面积公式求出了扇形的面积。这说明学生发现了扇形与三角形的相似性，很容易接受类比思想。另外，用相同的问题考查五年级已学过三角形面积的学生，甚至连扇形、弧、圆心角这些名词都没提，只是说明了表示弧的线有点弯曲，但弧上每一点与顶点的距离都相等，让学生借助相似性类比已学内容解决问题。结果两个班共112人中，有104人（占总人数的92.86%）用三角形面积公式求出了面积。这足以说明，教师可以根据学生的猜想直接指出“扇形的面积等于弧长与半径的乘积除以2”，或将弧长看成近似三角形的底，用“底乘高除以2”表示。这种处理方式既体现了课程标准在第二学段“数学思考”中倡导的“在观察、实验、猜想、验证等活动中，发展合情推理能力”的要求，又实现了三角形面积公式与扇形面积公式的统一性，有利于学生记忆和活学活用。因此，先学习扇形面积公式是可行的。

学生学了扇形面积公式后再去推导圆的面积公式就顺理成章了。可引导学生将圆分成（可等分也可不等分）几个扇形，求出每个扇形的面积后再求其和即可推导圆的面积公式。这样，既简单好懂，又省去了比较困难和烦琐的操作过程。

3.圆的面积估计与猜想的编写建议

对于圆的面积，是否需要先用方格纸或圆内接与外切正方形进行估计，提出猜想，再推导出圆的面积公式呢？浙教版、苏教版、西师大版教材编排了“估计—猜想—验证”，目的应该是体现课程标准在第二学段的“二、图形与几何”中，“（二）测量”之“5.会用方格纸估计不规则图形的面积“（第12页），以及 “在观察、实验、猜想、验证等活动中，发展合情推理能力”的要求。其实，课程标准并未明确要求在圆的面积部分体现，在其他内容中体现亦可，这也是其他教材都没有此设计，而是直接推导圆的面积公式的原因。当然，若教材能够渗透数学思想，体现科学发现的过程，对学生的发展还是有益的，但切忌机械式的操作计算。为此，提出以下建议：

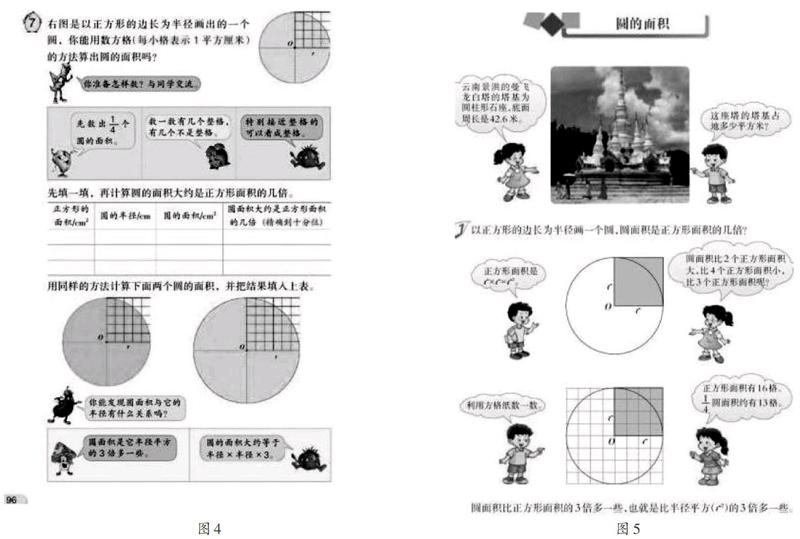
以苏教版教材（如图4）和西师大版教材（如图5）为例进行说明。由图可见，两个版本的教材都是先画一个正方形，再以正方形的一个顶点为圆心，以正方形的边长为半径画圆，然后用数方格的方法，数出四分之一圆的面积和正方形面积，进而得出圆的面积，最后计算出圆的面积是正方形面积的几倍，得到3倍多一些的结论，至此，都未引导学生提出猜想。

可见，该设计不仅有机械操作计算的问题，还存在着思路颠倒的问题。因为这里是探讨圆的面积问题，应该先画圆，再引导学生考虑圆的大小是由半径确定的，而度量面积的大小是用正方形做面积单位的，启发学生考察圆的面积是边长为圆的半径的正方形面积的几倍。这样，学生会作出相互垂直的直径，然后作出边长为圆的半径的正方形，进而比较。这不仅能促进学生思考，建立知识间的联系，更有利于学生思维与知识的拓展。如，在学生学习了圆的面积是相互垂直的两条半径构成的正方形面积的[π]倍后，教师给出相互垂直的长、短轴分别为2a、2b的椭圆，学生可以借助类比猜出椭圆的面积是以a、b为边长的长方形面積的[π]倍（[π]ab）。这样，既开阔了学生的思维，又体现了知识的活学活用。

用方格纸直接数出四分之一圆的面积有些困难，也不精确，很难提出猜想。对此，应让学生通过数方格得出其范围，再取平均值。这样，不仅渗透了两边夹逼的原则（高等数学中的两边夹法则）和极限思想，也体现了平均数的应用，更重要的是，可得到较为精确的数值，既有利于学生提出猜想，还展现了科学探究要精益求精的精神。例如，对于图4、图5中半径为4个单位长度的图形，学生通过拼凑可数出四分之一圆的面积在12与13之间，平均值为12.5，从而计算出圆的面积约为正方形面积的3.125倍。而若按西师大版教材（如图5）的“四分之一圆的面积是13”计算，得到的是3.25倍，误差之大可见一斑。又如，半径为5个单位长度的图形中，可数出四分之一圆的面积在19.5与20之间，平均值为19.75，计算出圆的面积约为正方形面积的3.16倍。由此两例，再引导学生联系圆的周长与直径的关系，学生便可猜出圆的面积是边长为圆的半径的正方形面积的[π]倍。然后，再指导学生将圆转化为扇形便可较容易地推导出圆的面积公式。

综上所述，无论是教材编写，还是教学实践，教师都必须考虑内容是否符合学生的认知水平，是否建立在学生已有知识的基础上。尤其是为了展现新课改理念的探究活动的设计，必须考虑其可行性和启发性。

【本文系“青蓝项目：青岛市教育学会 2018 年度教育研究项目——关于空间与图形领域课堂探索活动编写的比较研究（QES18E152）”研究成果之一。】

（责编 金 铃）