在确定单位和实际测量中建构面积概念

裴为堂

[摘 要]教学“面积和面积单位”时，有两处难点，一是怎么建立准确、稳固的面积概念，二是在制定面积单位时，选用什么作为面积单位，面积大小和面积单位的度量过程与结果有什么关联。教学时，教师应引导学生在面积单位确定和实际测量中有效建构面积的概念。

[关键词]面积;面积单位;概念; 测量

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）20-0033-02

对于“面积和面积单位”，教材进行了这样的描述：比较两个图形面积的大小要用统一的度量单位来测量。对此，笔者不禁质疑：三年级的学生，如果懂得用图形去度量图形，难道会不知道要统一度量衡，用统一规格的单位面积？除此之外，教材还提出一问题：“用何种形状的图形作为单位面积比较科学？”对于这一问题，笔者认为不论是从测量方便上考量，还是从学生的认知习惯来考虑，不同的测量对象应该采用不同形状的单位面积。比如一个大的等边三角形，恰好可以分割成整数个小等边三角形，此时用小等边三角形作为度量的单位面积正适合。教材上还提到：“选用正方形作为度量的单位面积最合适。”如果仅仅是度量长方形，选用正方形作为度量的单位面积固然方便，但长方形不就有得天独厚的优势吗？为了做出合理解释，许多教师创设了许多情境，并由此得出结论：正方形可以密铺，而长方形不能密铺。

一、概念教学策略确定

对于“正方形可以密铺，而长方形不能密铺”的观点，笔者不敢苟同。笔者认为，正方形也有“留缝”的时候，长方形也有可以密铺的时候。

“面积和面积单位”这一课的内容属于概念教学，而基础概念就应该让学生在生活中感受和提炼，或者在操作中体会，或者在解决困难时摸索。

“面积”的概念形成应该来自于度量面积的客观需要，辅之以一定量的辨析，学生对面积这个概念的认识就会更加理性、全面而深刻。因此，本着“不悱不发，不愤不启”的原则，笔者引导学生在解决问题的过程中揭露概念的本质。如果能让学生在解决问题的过程中产生一种热切渴望建立具有固定形状的度量标准的刚需，然后用单位面积的数量来计量待测物的面积大小，那么他的“面积单位”概念就会掌握得更加牢固。

当然，尺子是无法测量图形的面积的，但是不少学生却认为可先用尺子量出图形的长，再量出图形的宽，然后用“长乘宽”就能算出其面积的大小，而这都是尺子测量的“功劳”。但这并不是直接度量出待测物包含面积单位的数量，而是基于算术意义上的核计面积单位数量的简算方法。教师完全可以直接教学生这种算术意义上的面积计算方法，但果真如此做，学生也许终身都无法领悟面积单位的真谛，也无法理解长乘宽得出面积的始末。

长乘宽的确可以求出长方形的面积，学生只要量出长方形的长和宽，就可以计算出它的面积，照此说法，只要测量出三角形和梯形的关键线段的长度，就可以轻易求出它们的面积，但是这是测算，不是测量。这个过程是一个运用公式计算的过程，是一个物理换算的过程，是由长度推算出面积大小的过程，测量的原始量不是面积而是长度，不能算作直接度量面积。直接度量面积使用的测量工具应该包含面积单位，面积是二维平面内的几何量，所以测量工具应该是一个固定大小的平面而不是一个一维的长度，既然如此，测算出的面积自然就无法揭示面积的本质含义，也无法体现面积单位的本质属性。那么，测量长度有刻度尺，刻度尺本身就包含各种长度的线条，而且都标好了标准单位，那么测量面积有什么工具呢？显然，这个工具上需要标明面积单位的刻度。在寻找和创造面积度量工具和物色面积单位时，学生自然会对面积单位的属性做进一步思考并建立高级认识。

二、改进教案后的试教与反响

正是有了以上反思，笔者开始改进教案。首先引导学生触摸物体表面，感受其大小，然后让学生给这种平面的大小命名。学生会说出“面积”这个新词，此时学生对图形面积的认识还存在障碍（在两次教学中可见一斑），容易和周长混为一谈。因此，很有必要让学生指出面积的所在，以便和周长区分。比如三角形的面积在何处？需要引导学生指出三角形的三边包围的整个内部区域就是其面积，并让学生辨析面积和周长的区别。经过以上训练，学生对面积概念的掌握十分到位。在学生认清了物体表面的面积和图形的面积之后，再让其归纳总结面积的概念就水到渠成了。学生建立了面积的概念后，理解“面积单位”的含义就成了当务之急。笔者设计了面积大小的比较活动。先出示两组仅凭肉眼就能轻易看出大小的图形，一组是足球场和篮球场的对比图，另一组是需要叠放才能比较大小的组图（如图1），再出示一组靠直观观察和叠放都无法比较面积大小的图形，让学生自行钻研，攻克难题。学生可能会将首次叠再后露出来的部分都剪下来，继续叠放，循环往复，直到比出两个面积的大小。这不失为一个好办法，但不是最好，因为不但操作烦琐，而且破坏了图形的原形。

思维遇阻后，学生往往会想到测量法。要测量就需要测量工具，让学生自发物色测量工具，绝非易事，但也不是绝无可能。笔者先诱导学生说出用尺子测量，并在征求意见时形成两派争论之势，少部分学生会想到用图形来测量，而这个作为测量工具的图形的庐山真面目就是“面积单位”，只不过这个“面积单位”的大小未知，也没有得到广泛认可。为了与1平方厘米、1平方分米、1平方米的单位标准合拍，笔者引导学生从众多可供选择的单位形状中选出正方形。为了尽量避免人为操纵，笔者尝试同时使用正方形和长方形密铺，在“竞争”中突显正方形测量的优越性。

首次試教中，意外频发。学生认定长方形更合适，理由是1个长方形的面积刚好等于2个正方形的面积（失手造成的意外案例），如此一来，密铺完待测物后需要长方形的数量就最少，因此更合适。局面十分尴尬，但为了后面的教学，笔者拿出教师的绝对权威：正方形的四条边都一样长，测量起来更方便，更受欢迎（事实上，学生很反感）。学生屈服于笔者的权威，只好乖乖选用正方形。于是笔者安排小组用正方形去度量同一个长方形：有的小组拼摆的结果是24个小正方形，有的小组拼摆的结果是6个小正方形。这样就有了认知冲突，统一标准势在必行。但正方形多种多样，将哪一个定为标准合适呢？这就为下一课时的学习做好铺垫，体现了知识的连贯性。

三、课后的得失与争论

比如长方形面积的计算公式，就是建立在用1平方厘米大的正方形密铺图形时巧算正方形数量的基础上。对该内容，教研组也有一些争论，焦点就在“选用正方形测量最合适”上。教师都认为，没有最合适的单位形状，合不合适要因图而异。笔者再一次细细研读《教师教学用书》，发现书中有这样的描述：“教师应该明白，将面积单位规定为哪种形状、哪种尺寸，纯属人为规定。根据需要，选用其他形状，比如正五边形也并无不妥。”笔者一下子感到“沉冤得雪”，既然真相大白，那为啥教材还要说“选用正方形测量是最方便的？”，这背后一定有什么不得已的“苦衷”。

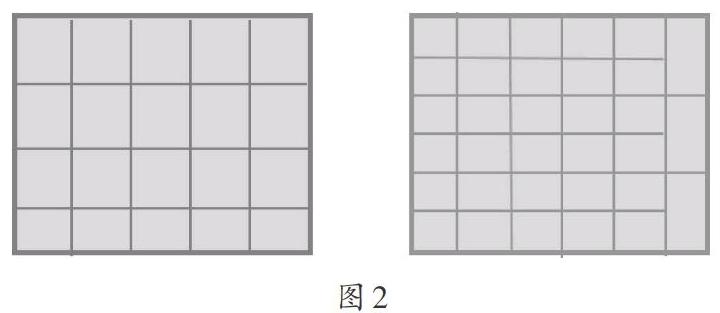
这个“苦衷”莫非就是为了确定1平方厘米、1平方分米、1平方米？用图形去测量图形的面积重要吗？笔者认为，这对学生创造出正确的面积单位，理解计算面积大小的真实原理来说很重要。但是，当我们理解了面积的计算原理后，谁还会去采用这种粗笨的图形密铺测量法呢？换言之，对于不同的图形应该因地制宜选用不同的单位面积形状，而实际上学生需要测量面积的图形就只有长方形，所以教材上说“选用正方形测量是最方便的”。那么为何要排除它的“兄弟”长方形呢？学生不是觉得长方形方便吗？笔者无心之失造就的一个特殊长方形（正好能分成2个正方形）倒提了个醒——应该选用更普通的长方形。思前想后，笔者决定做如下处理（如图2）。

该图形虽然没能杜绝巧合，但是普遍性更强了。同时直观上，也揭示了用4条边等长的正方形测量时的优势。这个处理在公开课中大放异彩，收到了意想不到的效果。

（责编 童 夏）