强化内在本质 修复知识断层
俞亚

[摘 要]“商不变规律”在有余数除法的应用中,对于余数的判断常常是难点。尤其是当遇到“300÷11○600÷22”这类比大小的习题时,学生的困惑就尤为明显:为何商一样,余数不一样,这两个算式却是相等的呢?要想突破这样的认知困惑,教师就要从知识的内在本质入手,借助直观手段,让学生明白余数的意义及其与除数的关系,无痕修复知识断层,最终破解教学难点。
[关键词]商;余数;除法;策略
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)20-0023-02
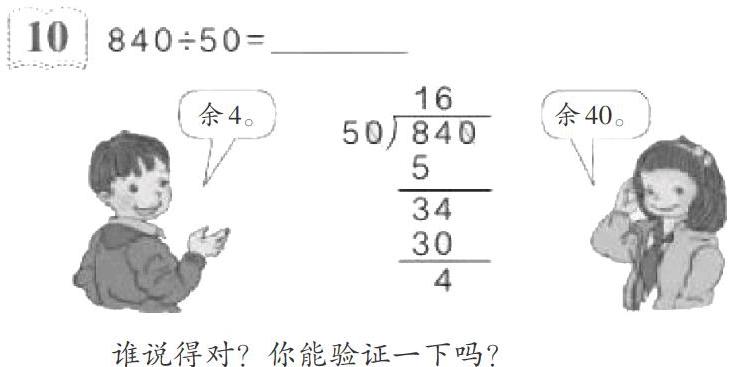
在四年级上册数学期末检测后,有一道习题的批改引起了一位学生的不解:“老师,这道题计算后明明是‘27……6>‘27……3,怎么是“=”呢?
经他这样一说,马上又有学生说:“您不是说过,‘实在看不出谁大谁小时,算一算不就知道了嘛。可算出来明明不一样,为什么填‘=却是对的?”
填“=”的学生站起来说:“左边式子的被除数和除数同时乘2,商不變,所以是等于……”
“不对!商虽然不变,但是余数变了,所以是不相等的。”在反对声中,原本认为相等的学生也开始动摇——虽然商不变,可余数的的确确不一样呀?两个算式还能用等号连接吗?
在学生的争论声中,笔者意识到了研究这个问题的必要性。
一、原因追溯
学生之所以对这道题存在争议,原因有三。
第一,所学知识的局限性。我们知道,判断结果是否相等,只要学习了小数除法,得到结果均是27.27,或用分数表示,结果都是300/11,那就可以确定是相等的。然而,现在学生还未学到小数除法和分数,只会用商带余数的方式来表示结果,结果的“同中有异”造成了学生的困扰。
第二,应试教育的副作用。在教学过程中,基于应试需求,我们有时会教给学生一些技巧来提高学生做题的正确率。尤其是在比大小一类的题中,有些学生不能利用观察来比出大小时,有的教师往往会说:“实在看不出谁大谁小,算一算不就知道了嘛。”在上例中,正是教师教给的应试技巧,学生放弃了用“商不变规律”来解决此题,而用了计算的方法,进而产生困惑。
第三,余数算理教学的简单化。这是问题产生的根源所在。学生应用“商不变规律”在有余数除法中进行简便计算时,教材直接采用讨论的方式展开。
我们看到,这里仅仅是让学生用验证的方法来解决“余数到底是多少”的难点。这样的教学,学生受到的是“被除数和除数同时除以10,商不变,余数变了”的强化记忆,却没有理解“为什么余数不一样”。算理教学的简单化为后续比大小埋下了“祸根”。
二、策略重构
那么,如何让学生利用现阶段的知识来解决文章开头所讲的困惑呢?笔者尝试进行了以下策略重构。
1.本质入手,借助直观,明晰余数所表示的含义
教学“商不变规律”在有余数除法中的简便计算时,对于“余数究竟是多少”,验算仅是一种表面的方法,实际上教师完全可以从本质入手——依托“计数单位”来给学生解惑。
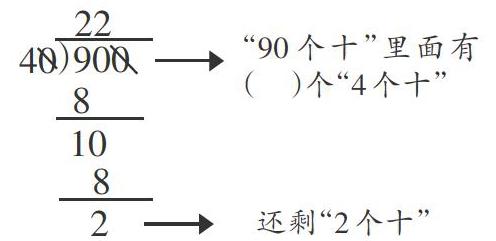
首先,可改变例题数据,换成900÷40,这样余数正好是除数的一半,学生更容易理解。告知学生,把900÷40看成90÷4来简便计算,实际上就是在求“90个十”里面有几个“4个十”。通过计算,学生发现有22个,还剩“2个十”。(如下图所示)
其次,还可以通过直观图,让学生理解900÷40进行简便计算后余数2所表示的意义,如下图所示。
通过计数单位来理解余数所表示的意义,对于后续学生学习小数除法来说,也是有很大帮助的。
2.提早介入,情境支撑,体会余数与除数的关联
900÷40与90÷4的余数不同,正反映出余数与除数的关联。因此,在学生理解了把900÷40看作90÷4来简便计算时,余数该如何判定之后,教师应及时介入,出示判断题:900÷40=90÷4=22……2。
学生很快就判断出这样写是错误的,原因是900÷40的商是22,但余数应该是20。此时,教师追问:“看来,这个等式错在最后一步,两个算式的商一样,余数却不一样,那么前面一步‘900÷40=90÷4对吗?”由此,暴露出学生的困惑:如果按照商不变规律,这两个算式是相等的,但是它们的余数不一样呀!商不变规律可以用在不能整除的除法算式中吗?这两个算式的结果到底相等吗?这就直接聚焦于文章开头提到的学生心中之困惑了。
那么,如何引导学生理解结果是相等的?我们可以依托现实情境来解决。
把“900÷40”看成900个苹果平均分给40个小朋友,把“90÷4”看成90个苹果平均分给4个小朋友,“900÷40”是否等于”90÷4”,就在于每个小朋友分到的苹果是否一样多。
如何求证两个情境中每个小朋友分到的苹果个数是否一样?两种情况都是每个小朋友分到了22个,即商是一样的,余数不同。剩下的苹果就不能整个整个分了,但如果要继续分的话,过程可以用下图来表示。
两个算式最终的结果都是22个苹果加半个苹果,等式成立。至此,教师追问:“为什么余数不一样,我们通过分苹果却发现实际结果是一样的呢?”让学生观察得到:余数是不能单独比较的,还要根据除数进行判断。就如同20个苹果看上去多,但它对应的是平均分给40个人,而2个苹果看上去少,但它对应的却是平均分给4个人,这两种情况其实结果是一样的。
至此,学生就会深刻体会,在比较有余数除法结果的大小时,不能孤立地看待余数,而应关注与余数相对应的除数,要从两者之间的关联进行分析。
3.有意渗透,告知后续,实现知识之间的有效衔接
当学生通过具体情境明白了余数与除数的关联之后,我们可以继续做一件事:“同学们,刚才通过分苹果,我们发现‘900÷40与‘90÷4的计算结果实际上是相等的,那么到底是不是这样的呢?我们可以用计算器来验证一下。”通过计算器验证,学生清晰地看到900÷40=90÷4=22.5,由此确定之前的推理是正确的。接着,教师可以明确告诉学生:“其实,等到了五年级,我们学习了小数除法以及分数表示商之后,就可以用小数或分数来表示商。”
通过上述环节,一方面让学生提前了解有余数除法中商的不同表示方法,感受知识的延续性;另一方面,再一次让学生明确“商不变规律”在有余数的除法算式中依旧成立。
三、反思感悟
学生出现的错误,很大程度上印证着教师在教学中的疏漏与欠缺。这是在本次问题提出与解决过程中笔者的最大感受。幸好“亡羊补牢,为时不晚”,通过上述环节的明理之后,学生深刻领会了为何“商不变规律”在有余数除法中同样适用以及该怎么使用的问题。至此,学习过程中出现的暂时性的“知识断层”被修复,教学难点也终于得到破解。
由此,笔者深切体会到,在开展教学的过程中,教师既要站在学生已有知识能力水平的基础上去设计教学,又要应用足够的知识储备来预设问题,及时发现学生在学习过程中存在的疑点与困惑,真正做到未雨绸缪、有的放矢地开展教学。教师要始终站在知识的本质角度出发,努力去寻求新旧知识的联结点,适度改编教材,创新教学手段,让学生的困惑真切地获得破解与落地。
当然,另外值得一提的是,在教学中,教师应该多一点关注学生思维能力的培养,把握每一道习题的用意与初衷,切不可一味追求结果,再用一些所谓的“应试小技巧”来限制学生的思维。
(责编 李琪琦)

