基于超声导波的管道缺陷监测及径向损伤评估*

徐 阳 罗明璋 杜国锋

(1.长江大学电子信息学院 2.长江大学城市建设学院)

0 引 言

油气管道服役环境复杂，外界冲击以及环境因素等容易引起管道变形、腐蚀和裂纹等缺陷[1-4]，一旦缺陷径向损伤深度达到贯穿管壁就会造成泄漏事故，严重危及企业生产和人民生命财产安全。为保证油气管道安全运行，对管道缺陷进行监测及径向损伤深度评估具有十分重要的意义[5-8]。应用超声导波进行管道缺陷监测具有效率高、成本低以及监测范围广等优点，在管道结构健康监测领域获得了广泛的应用[9-11]。

国内外学者对导波与管道缺陷的相互作用进行了大量研究。D.C.GAZIS[12-13]首先推导出了无限长各向同性圆管中导波传播的理论表达式，为导波在管道中的传播研究奠定了理论基础。A.H.FITCH[14]通过试验得到了管道内导波的群速度值，验证了D.C.GAZIS提出的理论解。D.N.ALLEYNE等[15-16]研究了纵向模态导波在管道裂纹缺陷上的反射现象。M.J.S.LOWE等[17]研究了导波在管道缺陷处的模态转换现象。在管道损伤初期出现的小缺陷，对于超声导波的反射回波信号很微弱，容易被其他噪声淹没而无法监测。利用时间反转技术可以提高超声导波对小缺陷的监测能力，大量研究成果为这一新技术提供了有益的参考[18-19]。时间反转法最早由法国科学家M.FINK[20]提出，该方法是将直接导波监测信号中的缺陷回波进行时间反转并重新激励出去，使导波能量在缺陷位置发生聚焦，增强缺陷反射回波的幅值从而有利于信号监测。邓菲等[21]研究了时间反转法在管道缺陷监测中的时空聚焦效应。周进节[22]研制开发了基于时间反转法的超声导波监测设备。符浩等[23]提出了一种合成相位聚焦方法，为工程应用提供了一种有效手段。XU Y.等[24]提出了一种基于时间反转和匹配追踪算法的管道缺陷定位方法。DU G.F.等[25]采用时间反转法进行了管道腐蚀坑监测试验并取得了理想的结果。

锆钛酸铅(PZT)是一种具有很强压电效应的陶瓷材料，本文采用PZT传感器阵列来激励和接收管道中的超声导波，利用时间反转法来提高管道缺陷监测能力，通过监测L(0,2)和L(0,1)模态缺陷反射系数的变化趋势来实现管道缺陷径向损伤深度的评估。基于传递函数思想分析了合成时间反转法实现导波能量在管道缺陷位置聚焦的原理，通过试验验证了合成时间反转法提高超声导波对管道缺陷监测能力的有效性。激励入射的L(0,2)模态导波在管道中传播时遇到缺陷,会与之相互作用而发生模态转换，产生L(0,1)转换模态导波。在管道缺陷监测过程中L(0,2)反射模态与L(0,1)转换模态都包含大量有用的缺陷信息。结合导波在管壁中的位移分布，分析了缺陷径向损伤深度对L(0,2)和L(0,1)模态转换的影响机理。随着径向损伤深度的扩展，L(0,2)模态缺陷反射系数呈现出单调增加的趋势，而L(0,1)模态缺陷反射系数则呈现出先增大后减小的变化趋势，当径向损伤深度达到半壁厚时，L(0,1)模态缺陷反射系数达到最大值，此后随径向损伤深度进一步扩展而逐渐减小，直到径向损伤深度达到贯穿管壁时，L(0,1)模态缺陷反射系数减小为0。通过试验得到的监测数据与分析结果一致，验证了本文提出的管道缺陷径向损伤深度评估方法的正确性和实用性。研究结果为判断管道缺陷径向损伤是否达到半壁厚或贯穿程度提供了重要参考。

1 管道中的导波特性

1.1 导波的多模态和频散特性

导波在中空管道内沿轴向传播时具有纵向模态、扭转模态和弯曲模态三种不同的形式。纵向模态和扭转模态关于圆管中心线呈轴对称，而弯曲模态则呈非轴对称。纵向模态用L(0,m)表示，m=1,2,3,……；扭转模态用T(0,m)表示，m=1,2,3,……；弯曲模态用F(n,m)表示，n、m=1、2、3、……。其中：n为导波的周向阶次，表示该模态导波沿管壁的传播形式；m为导波的模数，表示该模态导波沿壁厚方向的振动形式。一种模态的导波在管道中传播时遇到缺陷，会与缺陷相互作用而发生模态转换，产生一些新的模态。另外，提高激励信号的频率，也会使导波模态的数量增加。

D.C.GAZIS[12]通过对理论表达式的推导，提出了导波在无限长中空管道中传播的频散方程。对频散方程进行数值求解并绘制相应的频散曲线可以进行模态分析，掌握不同模态导波的径向和轴向位移分布，可为管道缺陷监测选择合适的模态以及工作频率范围提供理论依据。图1表示对外径76 mm、壁厚4 mm 的AISI304不锈钢管中导波传播的频散方程进行数值求解而得到的群速度和相速度频散曲线。

图1 外径76 mm、壁厚4 mm的AISI304不锈钢管的频散曲线Fig.1 Dispersion curve of AISI304 stainless steel pipe with 76 mm outside diameter and 4 mm wall thickness

由图1可见，轴对称纵向模态L(0,2)的群速度最快，并且L(0,2)模态在70～200 kHz频率范围内基本没有频散，在所有回波信号中L(0,2)模态将最先到达接收传感器且波形不会发生畸变，因此选用L(0,2)模态导波来进行管道缺陷检测可以取得较为理想的效果。

通过编程和数值计算，可以绘制出不同模态导波在管壁中的位移分布。当给定频率120 kHz时，管壁中L(0,2)模态和L(0,1)模态的位移分布如图2所示。由图2a可见，L(0,2)模态的轴向位移沿管道壁厚呈均匀分布且幅值相对较大，有利于监测管道横截面上任意位置的缺陷损伤。L(0,2)模态沿管壁的径向位移相对较小，在传播过程中能量泄漏少，适合于长距离传播。当激励信号沿管壁轴向振动时，将在管道中产生L(0,2)模态导波。

图2 频率为120 kHz时L(0,2)和L(0，1)模态的位移分布Fig.2 Displacement distribution of L(0,2) and L(0,1) modes at 120 kHz frequency

由图2b可见，L(0,1)模态的轴向位移沿管道壁厚呈不均匀分布状态，并且同时存在正向和反向的轴向位移。正是由于这种正、反方向轴向位移的存在，导致管道缺陷沿径向深度扩展时，L(0,1)转换模态导波的幅值呈现出一种有规律的变化趋势，为管道缺陷径向损伤深度评估提供了重要参考。L(0,1)模态沿管道壁厚的径向位移相对较大，当激励信号沿管壁径向振动时将在管道中产生L(0,1)模态导波。

采用长度伸缩型PZT压电片并使其沿管道轴向振动，同时选择PZT压电片的长度为特定频率下L(0,1)模态的波长，可以激励出单一的L(0,2)模态用于管道缺陷监测，同时可抑制激励过程中产生的L(0,1)模态[10-11]。由图1b所示的相速度频散曲线可知，当频率为120 kHz时，L(0,1)模态的相速度约为1 937 m/s，此时L(0,1)模态波长λ=1 937/(120×103)=16 mm，因此选用长度为16 mm的长度伸缩型PZT压电片组成激励传感器阵列，沿圆周均匀布置在管道的一端，然后对该阵列施加一个中心频率为120 kHz的汉宁窗调制正弦波信号，即可激励出管道中的L(0,2)模态导波用于缺陷监测。

1.2 管道缺陷径向损伤深度对L(0,2)与L(0,1)模态转换的影响

导波在管道中传播时遇到缺陷会发生模态转换，而缺陷的形状和尺寸特征对导波模态转换具有决定性的作用。当激励入射的L(0,2)纵向模态导波在带缺陷的管道中沿轴向传播时，在缺陷位置处会发生散射并且产生模态转换，部分L(0,2)模态将转换为F(n,m)弯曲模态和L(0,1)纵向模态，F(n,m)弯曲模态可以通过对沿管道圆周均匀布置的传感器阵列中各个传感器接收信号进行叠加而消除，而L(0,1)转换模态则将得到保留。下面说明缺陷径向损伤深度对L(0,2)到L(0,1)模态转换的影响。图3所示为管道缺陷对L(0,2)和L(0,1)模态在管壁中位移分布的影响示意图。如图3a所示，L(0,2)纵向模态导波在管道缺陷处产生反射，形成正向位移分量和反向位移分量。将缺陷处轴向位移零点位置标记为O，正向位移分量标记为A，反向位移分量标记为B。此时管壁中同时出现的正向和反向位移分量与L(0,1)模态十分相似，如图3b所示。对管道截面施加的激励载荷与某种导波模态在管壁中位移分布的相似程度越高，越容易激发出该模态的导波。

图3 管道缺陷对L(0,2)和L(0,1)模态在管壁中位移分布的影响Fig.3 Schematic diagram of influence of pipeline defects on displacement distribution of L(0,2) and L(0,1) modes in pipe wall

当L(0,2)模态导波沿带缺陷的管道轴向传播时，在遇到缺陷之前管壁中只有一个均匀向前的正向位移分量，此时不会出现L(0,1)模态。当遇到缺陷时，L(0,2)模态导波会发生散射，一部分L(0,2)模态继续向前传播，仍表现为正向位移分量A；另一部分L(0,2)模态则从缺陷处发生反射而向后传播，表现为反向位移分量B。此时管壁中的位移分布与L(0,1)模态相似，因此部分L(0,2)模态将在缺陷处转换成L(0,1)模态。如果管道中没有缺陷，反向位移分量B为0；如果管道中的缺陷达到穿透管壁的程度，则正向位移分量A为0。在这两种情况下，管壁中的位移分布均与L(0,1)模态的轴向位移分布不一致，因此不会发生L(0,2)到L(0,1)的模态转换。由此可见，只有当管道中存在未贯穿管壁的缺陷时，管壁中同时出现正向位移分量A和反向位移分量B，与L(0,1)模态的轴向位移分布相一致，此时缺陷处的反射信号中将包含L(0,1)转换模态。

图4为管壁中L(0,1)转换模态随管道缺陷径向深度扩展的变化趋势。如图4a所示，当缺陷径向深度为0(无管道缺陷)时，由于管壁中只有正向位移分量A，此时将不会出现L(0,1)转换模态。随着缺陷沿径向深度扩展，反向位移分量B逐渐增大，管壁中的位移分布逐渐与L(0,1)模态相匹配，导致L(0,1)转换模态逐步出现，使得L(0,1)转换模态导波的幅值随着管道缺陷径向深度的增加而逐渐增大。

如图4b所示，当缺陷沿径向深度扩展达到半壁厚时，正向位移分量A和反向位移分量B均达到与L(0,1)模态轴向位移分布最高的相似度，此时L(0,1)转换模态导波的幅值将达到最大值。如图4c所示，当缺陷沿径向深度逐渐扩展到穿透管壁时，反向位移分量B将持续增加到最大值，而正向位移分量A则将减小到0，正、反向位移分量与L(0,1)模态轴向位移分布的相似度逐渐降低，相应地，L(0,1)转换模态导波的幅值将逐渐减小并最终变为0。以上整个过程中L(0,1)转换模态导波的幅值将随着管道缺陷径向深度的增加而呈现出先增大后减小的变化趋势，这一特征对于评估管道缺陷径向损伤深度具有重要意义。

图4 L(0,1)转换模态随缺陷径向深度扩展的变化趋势Fig.4 Variation trend of L(0,1) conversion mode with radial depth expansion of defects

2 合成时间反转法聚焦原理

利用导波进行管道缺陷监测时，管道中的缺陷可以看作一个新的被动导波源[17]，它在反射激励模态导波的同时，还会产生许多新的转换模态。采用时间反转法可以使多种模态导波同时到达缺陷位置，实现导波能量在管道缺陷处聚焦，增强缺陷反射回波的幅值，从而提高管道缺陷的监测能力[18]。通常，时间反转法需要采用多通道同步激励-接收系统来完成多路信号的同步激励和接收，既复杂又不方便，而且实现起来还具有一定难度。本文采用一种新的合成时间反转方法，利用简单的单通道激励-接收设备，通过反复多次激励和接收过程获得多组数据，然后通过信号处理方法等效实现多通道同步激励-接收系统的时间反转聚焦功能[19]。

如图5所示，(zD,θD,rD)表示管道缺陷，N个传感器沿管道圆周均匀分布组成传感器阵列EN，(zi,θi,ri)与(zk,θk,rk)分别表示阵列中传感器Ei和Ek(i，k=1,2,3，……，N)的中心位置。通过传感器阵列同步激励得到的超声导波沿管道向前传播，到达缺陷处时，会发生散射和模态转换。此时缺陷可视为一个新的导波源，以反射波的形式向外发射超声导波，并沿着管道反向传播回传感器阵列。阵列中传感器Ek接收到的信号如下：

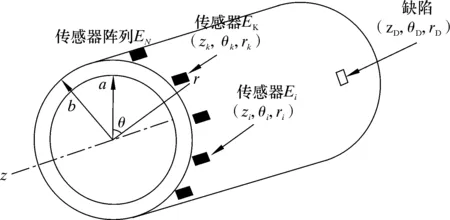
图5 带有缺陷和传感器阵列的管道示意图Fig.5 Schematic diagram for pipeline with defects and sensor arrays

(1)

式中：HDk(ω)为缺陷(zD,θD,rD)到传感器Ek的传递函数；S1(ω0)为初始激励信号的傅里叶变换；HiD(ω)为由传感器Ei到缺陷(zD,θD,rD)的传递函数；N为阵列中传感器的个数。

超声导波在管道中传播时满足互易定理，根据时间反转法[16-17]，在时域内对信号进行反转相当于在频域内对信号取复共轭。因此由传感器Ek接收信号生成的时间反转信号为：

(2)

式中：*表示复共轭, 下标TR表示时间反转信号，τ为保证因果关系所需的总延迟时间。

总共生成N个时间反转信号，将所有N个时间反转信号通过相应的传感器再次同步激励，到达缺陷处的时间反转聚焦信号为：

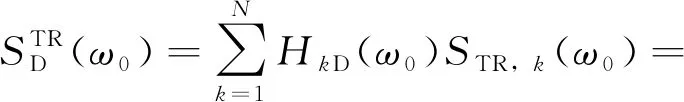
(3)

式中：HkD(ω0)为由传感器Ek到缺陷(zD,θD,rD)的传递函数。

整个传感器阵列接收到的最终时间反转聚焦信号可表示为：

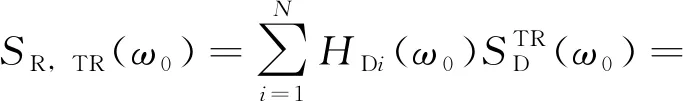
(4)

式中：HDi(ω0)为由缺陷(zD,θD,rD)到传感器Ei的传递函数。

令：

(5)

则式(5)可重新表示为:

(6)

3 试验验证

取一根外径76 mm，壁厚4 mm，长度2 000 mm的AISI304不锈钢管作为试验管道，如图6所示。在距离管端800 mm处设置一个周向槽形裂纹缺陷，缺陷深度1 mm，轴向宽度2 mm，周长35 mm。在管道一端外表面均匀布置2个PZT传感器阵列，分别用于激励和接收超声导波，阵列之间轴向距离为1mm，每个阵列包含16个尺寸为16 mm×3 mm×1 mm的长度伸缩型PZT压电陶瓷晶片，陶瓷晶片的机电耦合系数k31为0.38，压电常数d31为-210 C/N，频率常数为2 000 Hz·m。这种布置可以在管道中激励出单一的L(0,2)模态导波，并且易于压制F(n,m)弯曲模态导波[10-11]。管道缺陷与传感器阵列布置如图7所示。

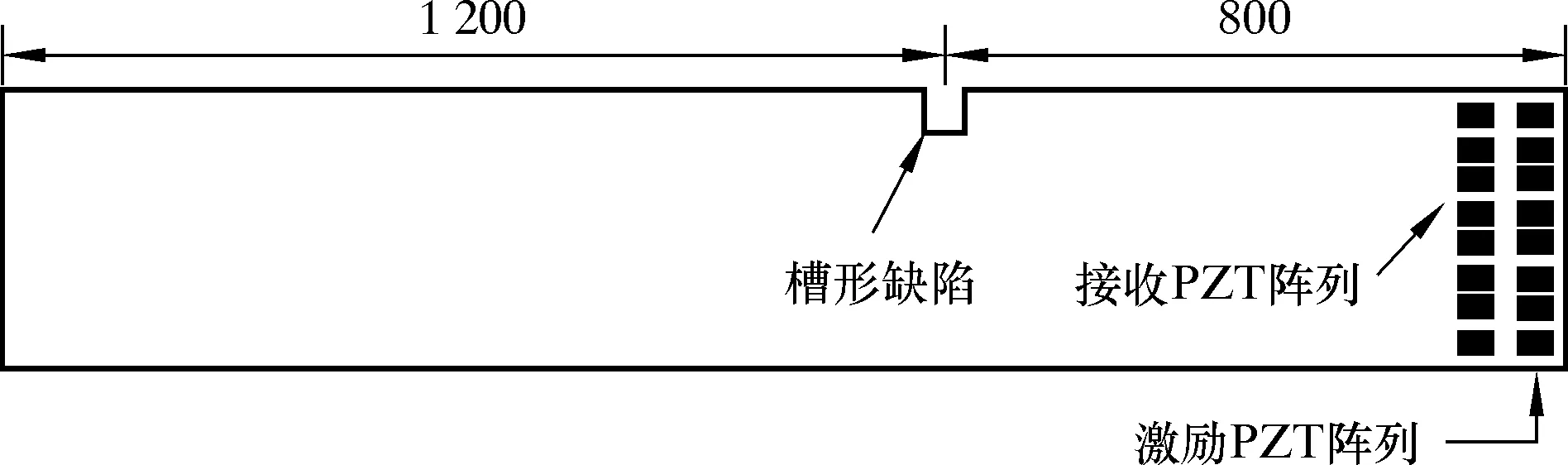
图6 试验管道示意图Fig.6 Schematic diagram of test pipeline

图7 管道缺陷与传感器阵列布置Fig.7 Pipeline defects and arrangement of sensor arrays

试验仪器主要包括任意波形发生器(SDG2122)、功率放大器(ATA2021H)、数字示波器(MSO2014)以及用于信号处理的计算机。AISI304试验管道采用木质支架支撑。采用直接导波法对管道缺陷进行监测。由任意波形发生器产生120 kHz汉宁窗调制10周期正弦信号，通过功率放大器放大，同步加载到激励传感器阵列中的16个PZT压电片上，激励出管道中的L(0,2)模态导波。导波沿管道向前传播时遇到缺陷会发生模态转换同时产生反射回波，回波信号被接收传感器阵列中的PZT压电片所接收，并通过数字示波器进行采集，共采集16个PZT压电片的信号。通过数字存储示波器从单个接收PZT压电片采集得到的信号如图8所示。

图8 单个接收PZT压电片上的信号Fig.8 Single signal received on PZT piezoelectric plate

由图8可见，信号波包较为复杂，其中除了L(0,2)反射模态之外，还包含有L(0,1)以及F(n,m)等转换模态信号。将沿管道圆周均匀布置的接收传感器阵列中所有PZT压电片获得的信号进行叠加，可以消除F(n,m)转换模态的影响[28]。对16个PZT接收压电片获得的信号进行叠加并进行幅值归一化处理，结果如图9所示。

由图9可见，在L(0,2)激励信号与尾端回波之间呈现出了两个信号波包，而在管道中只设置了一个缺陷。根据图1频散曲线中L(0,2)和L(0,1)模态导波的群速度，结合图9中信号波包出现的时域位置进行分析，第一个波包为管道缺陷反射的L(0,2)模态，第二个波包为L(0,2)激励模态与管道缺陷相互作用而产生的L(0,1)转换模态。另外,从图9还可以看到，对于径向损伤深度为1 mm的管道缺陷，采用直接导波法监测得到的L(0,2)和L(0,1)信号波包幅值都很小，在实际应用中可能被噪声淹没而无法识别。

图9 全部接收PZT压电片信号的叠加结果Fig.9 Superposition results of all PZT piezoelectric plate signals received

为了提高超声导波对管道缺陷的监测能力，采用合成时间反转法来进行管道缺陷监测试验。如图8所示，对每个接收PZT压电片获得的监测信号，用一个适当的信号截取矩形窗，从相同的时间起点进行信号截取，截取内容包括L(0,2)反射模态和F(n,m)转换模态波包信号，记为f(t)。对每一个截取得到的波包信号进行时间反转处理，生成16个时间反转信号fTR(t)，且满足fTR(t)=f(τ-t)，其中τ为信号截取矩形窗的宽度。将每个时间反转信号通过激励PZT传感器阵列中与接收PZT压电片圆周位置相同的激励PZT压电片重新激励，共激励16次。每次激励后，都要通过数字示波器从接收PZT传感器阵列中记录16个接收信号，总共获得16×16个接收信号，最后对全部接收信号进行叠加求和，得到等效的多通道同步激励-接收系统的时间反转聚焦信号，经过幅值归一化处理之后的时间反转监测结果如图10所示。

与图9比较，时间反转监测信号中L(0,2)和L(0,1)模态的幅值都得到明显提高。定义缺陷反射系数为缺陷反射回波波包峰峰值与激励波包峰峰值之比，则采用直接导波监测获得的缺陷反射系数为0.016 9，而采用时间反转导波监测获得的缺陷反射系数为0.086 3，放大了4倍多。可见在管道缺陷超声导波监测中采用时间反转技术可有效增强监测信号的信噪比，提高管道缺陷监测能力。

由图10可见：随管道缺陷径向深度的扩展，L(0,2)反射模态幅值呈单调增长的趋势，而L(0,1)转换模态幅值则呈现出先增大后减小的趋势；当缺陷径向深度达到贯穿管壁时，L(0,1)转换模态幅值变为0。这一特征与1.2节中关于管道缺陷径向深度变化对L(0,2)和L(0,1)模态影响的理论分析一致，说明在管道缺陷监测过程中利用L(0,2)和L(0,1)模态的变化趋势进行缺陷径向损伤深度评估切实可行。

4 监测结果分析

4.1 缺陷损伤沿径向深度扩展时L(0,2)和L(0,1)模态导波的反射特征

为了定量反映管道缺陷损伤沿径向深度扩展时L(0,2)和L(0,1)模态导波的反射特征，将缺陷周长固定为管道周长的20%，并将缺陷径向深度分为10个等级，从10%壁厚扩展到100%壁厚，增量为10%壁厚。在120 kHz激励信号下采用时间反转法进行缺陷监测试验，获得不同缺陷径向深度下L(0,2)和L(0,1)模态导波的缺陷反射系数，监测结果如图11所示，其中圆形标注曲线为L(0,2)模态缺陷反射系数，正方形标记曲线为L(0,1)模态缺陷反射系数。由图11可知：随着缺陷沿径向深度的扩展，L(0,2)模态缺陷反射系数单调增加，而L(0,1)模态缺陷反射系数先增大后减小；在缺陷径向深度达到半壁厚前，L(0,2)和L(0,1)模态缺陷反射系数几乎相同；当缺陷径向深度达到50%壁厚时，L(0,1)模态缺陷反射系数达到最大值；随着缺陷径向深度进一步扩展，L(0,1)模态缺陷反射系数逐渐减小，而L(0,2)模态缺陷反射系数仍继续增加；当缺陷径向深度达到贯穿整个管壁时，L(0,1)模态缺陷反射系数减小到0，而L(0,2)模态缺陷反射系数达到最大值。可见，通过监测L(0,2)和L(0,1)模态缺陷反射系数的变化趋势，可有效评估管道缺陷径向损伤深度，从而判断损伤是否达到50%壁厚或贯穿程度。

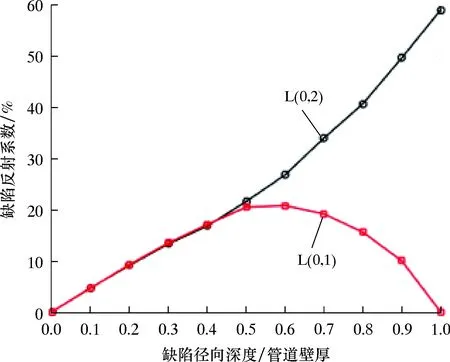
图11 L(0,2)和L(0,1)模态缺陷反射系数沿缺陷径向深度扩展的变化曲线Fig.11 Variation curve of defect reflection coefficients ofL(0,2) and L(0,1) modes along radial depth expansion of defects

4.2 缺陷损伤沿管道周向扩展时L(0,2)和L(0,1)模态导波的反射特征

缺陷径向深度固定为壁厚的70%(即非贯穿缺陷)，将缺陷周向长度分为10个等级，从管道周长的10%扩展到100%，增量为10%管道周长。在120 kHz激励信号下采用时间反转法进行缺陷监测试验，获得不同缺陷周向长度下L(0,2)和L(0,1)模态导波的缺陷反射系数，监测结果如图12所示，其中圆形标注曲线为L(0,2)模态缺陷反射系数，正方形标记曲线为L(0,1)模态缺陷反射系数。由图12可知，L(0,2)和L(0,1)模态缺陷反射系数随缺陷周向长度的增加都呈现出非线性增加趋势，开始时增加较快，然后逐渐变慢而趋于一个常数值。这是因为采用时间反转法进行管道缺陷监测，不同模态的导波能量会在管道缺陷处发生聚焦。随着缺陷周向长度的增加，导波能量将沿周长逐渐分散。当缺陷沿周向长度进一步扩展达到整个管道周长时，导波能量将均匀地分布到整个管道圆周之上。

图12 非贯穿缺陷L(0,2)和L(0,1)模态缺陷反射系数沿周向长度扩展的变化曲线Fig.12 Variation curve of defect reflection coefficients of L(0,2) and L(0,1) modes with non-penetrating defects along circumferential length expansion

缺陷径向深度固定为壁厚的100%(即贯穿型缺陷)，在120 kHz激励信号下采用时间反转法进行缺陷监测试验，获得不同缺陷周向长度下L(0,2)和L(0,1)模态导波的缺陷反射系数，监测结果如图13所示，其中圆形标注曲线为L(0,2)模态缺陷反射系数，正方形标记曲线为L(0,1)模态缺陷反射系数。由图13可知，L(0,2)模态缺陷反射系数随缺陷周向长度的增加呈现出非线性增加趋势，而L(0,1)模态缺陷反射系数近似为0。

图13 贯穿型缺陷L(0,2)和L(0,1)模态缺陷反射系数沿周向长度扩展的变化曲线Fig.13 Variation curve of defect reflection coefficients of L(0,2) and L(0,1) modes with penetrating defects along circumferential length expansion

可见，只有对于管道中的非贯穿缺陷，L(0,2)模态导波在管道中传播时才会发生L(0,2)到L(0,1)的模态转换，而对于贯穿型缺陷则不会发生这种模态转换。该特征与1.2节中关于L(0,2)到L(0,1)模态转换的分析一致，这也是管道缺陷径向损伤深度评估的另一个重要参考依据。

5 结 论

(1)采用叠加合成的方法，利用单通道装置进行多次激励和接收信号操作，等效完成了多通道同步激励-接收时间反转信号的功能，实现了导波能量在管道缺陷处聚焦，使缺陷反射回波幅值明显增强，特别是对于损伤早期的小裂纹缺陷，可以有效提高监测信号的信噪比。

(2)L(0,2)模态导波沿带有缺陷的管道传播时，由于管壁出现与L(0,1)模态相似的轴向位移分布，导致部分L(0,2)模态转换为L(0,1)模态。随着缺陷径向损伤深度扩展，L(0,2)与L(0,1)模态缺陷反射系数分别呈现不同的变化规律。

(3)只有非贯穿管道缺陷才会发生L(0,2)到L(0,1)的模态转换，对于贯穿型缺陷则不会发生这种模态转换。

(4)对于非贯穿缺陷损伤，通过监测L(0,2)和L(0,1)缺陷反射系数的变化趋势，可以有效评估管道缺陷径向损伤的深度，判断缺陷损伤是否达到半壁厚或贯穿程度。