基于多特征的APSO-SVR的模拟电路故障预测

王 力，龚振东

(1.中国民航大学 职业技术学院，天津 300300；2.中国民航大学 电子信息与自动化学院，天津 300300)

模拟电路是指用来对连续时间信号进行传输、变换、处理和放大等工作的电路，被广泛用于民航、医疗和军事等领域的电子系统中，当模拟电路发生故障时会导致整个系统无法正常运行.为了提高模拟电路的可靠性，需要对模拟电路进行故障预测与健康管理(Prognostics and Health Management，PHM)的研究[1].模拟电路的PHM 包括故障诊断与故障预测，在故障诊断领域的研究取得了较好的成果[2].

模拟电路的故障预测旨在精准地估计其剩余使用寿命(Remaining Useful Life,RUL)，故障预测的主要方法为建立模型的方法与数据驱动的方法.相较而言，数据驱动的方法计算简单且能获得不错的效果[3]，其中较典型的有支持向量机[4]、超限学习机[5]和相关向量机[6]等机器学习方法，均被成功地应用到模拟电路的故障预测领域.文献[7]提取模拟电路的频率特征进行故障预测.文献[8]提取被测电路电压信号并计算余弦距离进行故障预测.文献[9]提出了一种多核相关向量机方法对测试元件的故障发生时间开展预测.支持向量机回归(Support Vector Regression，SVR)是当前比较成熟的机器学习方法的理论，凭着实用性强、训练样本小、泛化能力好等优点[10-11]，在故障预测方面优势突出，已被学者成功应用于多种领域.文献[12]通过BFOA 算法对SVR 模型进行参数优化，最后基于优化模型开展温度预测.文献[13]用粒子群(Particle Swarm Optimization，PSO)算法优化SVR对多联机功耗进行预测，取得不错的效果.文献[14]指出SVR 中的惩罚因子C，核函数参数 γ 对回归预测精度有着很大的影响.SVR 通常使用网格搜索法来确定惩罚因子C与核函数参数 γ，但是网格寻优步长选取过大会导致模型预测精度低，步长过小会使优化运算时间过长，实际的使用效果并不好.

本文拟将被测电路的输出的统计特征和小波包分解能量特征作为特征向量，然后利用欧式距离量化电路退化的状态建立故障指示器，最后用自适应粒子群算法优化的支持向量回归预测模型进行模拟电路的故障预测，估算电路的RUL.利用基准电 路进行仿真实验以验证方法.

1 模拟电路的故障特征提取

1.1 特征向量提取及预处理传统的特征提取方法设置模拟电路的输入为扫频激励源，只考虑统计特征里的单一响应电压作为输入特征，无法充分反映电路的实时退化状态[15].与传统方法不同，小波包分解能对时间频率进行局部分析，通过对信号的平移伸缩实现低频段的频率细分和高频段的时间细分[16]，实现对信号的自适应分析.因此，本文用多个统计特征和小波包分解后的能量特征融合的方式来构造故障指示器.

首先，选取均值、峰值、峭度、方差4 个常用统计特征构成模拟电路的统计特征向量.均值a表示数据的平均趋势；峰值p是电流、电压或功率的最大瞬间值；峭度ku是归一化的四阶中心距，其大小跟电路的故障程度有关，值越大偏离初始状态越远；方差u用来衡量数据和其均值之间偏离的程度.其公式分别定义如下：

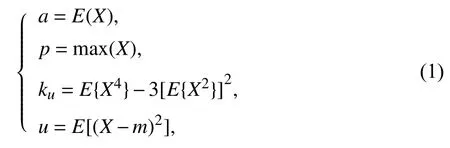
式中，X为模拟电路的输出响应，E是取期望值，max 是取最大值.

其次，利用小波分解对电路输出数据进行分解，用4 层小波包将信号分解成如图1 所示的16 个子频带.电路输出变化会影响各分量的能量值，这些能量值包含了模拟电路的状态信息.因此计算各子频带的能量值用来构建故障特征向量，其步骤如下：

图1 小波包分解图Fig.1 Diagram of wavelet packet decomposition

步骤 1对经过4 层小波包分解的子信号能量进行如下计算：

式中，xjn为各分解信号的幅值.

步骤 2计算分解后自信号的总能量

步骤 3进行能量归一化处理

步骤 4构造模拟电路故障预测输出能量的特征向量

式中，h1到h15分别表示各分量的能量值.最后，将电路的统计特征和小波包的能量特征分别表示为G={g1,g2,g3,g4}和H={h0,h2,···,h15}.其中g1,g2,g3,g4分别表示均值、最大值、峭度和方差这4 个统计特征向量.将统计特征和小波包特征进行融合，得 到特征向量F={G,H}.

1.2 故障指示器生成故障指示器(Fault Indicator，FI)是反映电路性能退化的指标，其数值会随着电路性能的衰退而升高.本文采用欧氏距离来衡量模拟电路元件退化前后特征向量间的相似度，构建故障指示器以表征电路退化程度.

2 APSO-SVR 的故障预测模型

2.1 SVR 理论SVR 以支持向量机分类问题中的超平面决策边界作为回归模型[17].对于非线性数据集{xi,yi}(i=1,2,···,m)，xi为样本输入，yi为样本输出，将样本从低维空间映射到高维空间的公式如下：

式中，ω 为法向量，b为位移项，ϕ(xi)是xi映射后的特征向量.

训练支持向量回归模型的过程就是寻找最优ω,b使f(xi)尽量逼近yi，然后转化成一个凸二次规划的问题，其形式为

最后引入满足Mercer 条件的核函数K(x,xi)=ϕ(xi)，得到SVR 的回归模型如下：

其中，核函数K(x,xi)对应的是x与xi映射到特征空间的内积，可以代替特征空间内的复杂运算.

核函数会对SVR 模型的性能产生较大影响，模拟电路的故障预测是多因子影响的非线性问题，采用径向基核函数的SVR 可以更好地处理模拟电路故障预测数据的非线性问题且拥有良好的泛化能力.因此本文中的SVR 模型采用径向基核函数，其计算公式如下：

式中，γ 是决定映射数据在特征空间中位置的核函数参数，其值与支持向量数成反比.

实际采用SVR 进行模拟电路故障预测时，如使用网格搜索法来确定SVR 的惩罚因子C与核函数参数 γ，难以确定合理的参数搜索范围与步长，对故障预测的准确度影响很大，因此本文考虑使用APSO 算法来确定SVR 的惩罚因子与核函数参数，以提升模型预测精度.

2.2 APSO 算法PSO 算法属于人工智能算法，它有收敛速度快、易实现、调整参数不多、全局搜索能力强等特点[18].但是，PSO 算法也有容易提前收敛、搜索精度不高、后期迭代效率低等不足.因此，本文使用APSO 优化算法进行参数寻优，以得到更高的拟合精度，并避免陷入局部最优.

首先，初始化粒子群的种群参数，并计算每个粒子的适应度作为衡量标准.每个粒子根据个体极值和全局极值来更新速度和位置其公式如下：

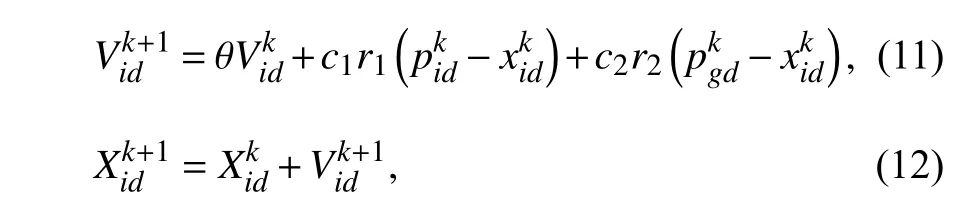
式中，k为迭代次数，θ 为用于调整模型寻优性能的惯性因子，id表示第i个粒子的第d维，gd表示id找到的全局极值，学习因子c1、c2分别为调节单个粒子搜寻局部最优位置方向和全局最优位置方向的步长，r1和r2为服从 [0,1] 均匀分布的随机数.

通过更新粒子当前位置得到SVR 中待求参数C和γ的最优解.在这个过程中，如果粒子的速度一直保持较大值，则在单次迭代中会导致粒子活动的范围过大，跳出最优解的区域.为使粒子的飞行速度随着迭代次数的增加而减小，本文通过改变影响速度的参数c1,c2和惯性权重 θ，间接实现粒子飞行速度的调整.

其中，设定c1从2.5 非线性减小到1.5，c2从2.1 非线性减小到1.1，计算公式如下：

式中，n为当前迭代次数，nmax为最大迭代次数.

惯性权重 θ 是粒子群算法中影响调整全局与局部寻优能力的关键参数，其在较大时表现出较强的全局寻优能力，较小时表现出较强局部寻优能力.为满足不同进化阶段的搜索需求，θ 应随着迭代次数的增加而逐步递减.因此，本文引入自适应惯性权重调整法，其公式为：式中，f为每个粒子的当前适应度，fmin为所有粒子 的最小适应度，favg为所有粒子的平均适应度.

2.3 APSO-SVR 模型使用APSO 算法迭代寻优得到SVR 的最优参数，得到模拟电路预测模型，具体步骤如下所示：

步骤 1将FI 中的训练数据作为输入;

步骤 2确定初始粒子群的相关参数，应用APSO 算法对SVR 中的参数C和γ进行寻优，其中参数C和γ的搜索范围均为 [2-8,28];

步骤 3粒子适应度的计算与对比，以SVR的预测均方差函数作为目标函数，计算并比较各个粒子的适应度值，找到全局最优适应度值;

均方差计算公式如下：

式中，η=1,2,···,L，L是用于训练的数据量，z(η) 表示真实数据，y(η) 为预测数据.

步骤 4根据式(11)～(14)更新粒子;

步骤 5满足条件或达到迭代上限后输出SVR最优组合参数C和 γ.

其模型构建流程如图2 所示.

图2 APSO-SVR 预测模型构建流程Fig.2 Construction process of APSO-SVR prognostic model

3 实验与分析

为测试本文构建的模拟电路故障预测模型性能，针对一个具体模拟电路进行故障预测实验.

3.1 仿真实验以Sallen-Key 带通滤波器电路为故障预测对象，测试本文构建的APSO-SVR 模拟电路故障预测模型的性能.如图3 所示，电阻和电容的容差分别设置为5%和10%，故障阈值设置为其参数值偏离标称值的50%.

图3 Sallen-key 带通滤波器电路图Fig.3 Circuit diagram of sallen-key bandpass filter

选择电阻R3 和电容C2 为实验对象，设定其在退化过程中的参数值在每一个时间节点变化一次，电路交流扫频的起始频率为1 Hz，终止频率为100 kHz.电阻R3 从2 kΩ 逐步升高至3.2 kΩ，设置其以自身正常值的4%递增，得到150 个时间节点.电容C2 从5 nF 逐步升高至8 nF，设置其以自身正常值的4%递增，得到150 个时间节点.R3、C2 在参数值分别为3 kΩ、7.5 nF 时达到故障阈值，此时是第125 个时间节点，判定电路元件即将发生故障.

对样本数据进行划分，将R3 和C2 的前80 个时间节点的样本划分为训练样本，用于训练APSOSVR 故障预测模型，其余样本划分为测试样本，用于测试模型的故障预测性能.

根据Sallen-key 带通滤波器电路的输出数据，提取统计特征和小波包能量特征.经4 层小波包分解后得到如图4 所示的子频带波形图，然后计算其能量值，构建小波包能量特征向量，并与统计特征进行融合.

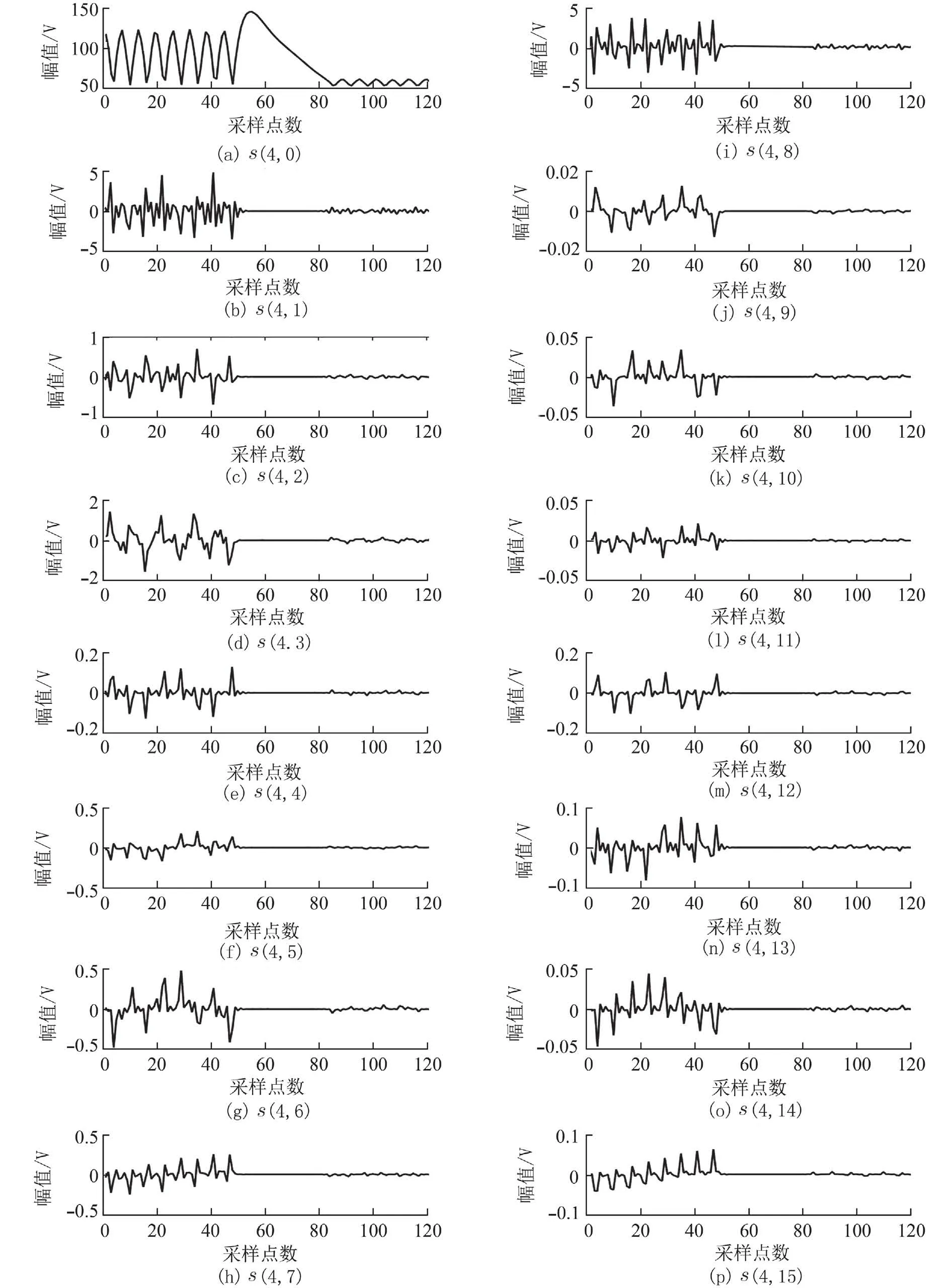
图4 子频带波形图Fig.4 Waveform diagram of sub-band

融合后的特征向量通过欧式距离公式计算得到故障指示器，其中，电阻R3 在各个时间节点的故障指示器如图5所示，曲线的变化趋势显示使用欧氏距离得到的故障指示器可以较准确地表征元件的性能退化轨迹.图5 中电阻R3 在第125 个时间节点时电路发生故障，其故障阈值为0.864 45.用相同的方法计算能得到电容C2 的故障指示器，其故障阈值为0.868 11，当故障指示器值大于或等于该阈值时即判断模拟电路发生故障.

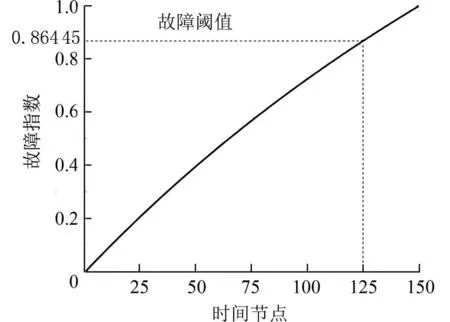
图5 R3 故障指示器Fig.5 The fault indicator of R3

设置电容和电阻2 个仿真实验：R3-80 和C2-80，即分别以R3 和C2 前80 个故障指示器数据作为训练样本输入到SVR 预测模型中进行参数训练.初始化粒子群参数，将APSO 的种群数量设定为20，最大迭代次数为100，进行迭代寻优找到S VR 的最优组合参数C和γ，其参数如表1 所示.

表1 SVR 组合参数Tab.1 Combination parameters of SVR

3.2 预测结果与分析评价指标采用剩余使用寿命预测值Res、绝对误差EA和均方差EMS，其公式如下：

式中，Res为预测剩余使用寿命，R为实际剩余使用寿命.

采用APSO-SVR 模型对Sallen-Key 带通滤波器电路中的电阻R3 和电容C2 进行故障预测，其结果如图6 和图7 所示.其中，均方差分别为6.431×10-5和5.301×10-5，较小的均方差 表明2 个仿真实验的预测数据和真实数据之间的偏离度较小，能够较为精确的预测出两元件的退化轨迹.

图6 R3-80 的APSO 优化后预测值和真实值Fig.6 Prediction and real value of R3-80 after APSO optimization

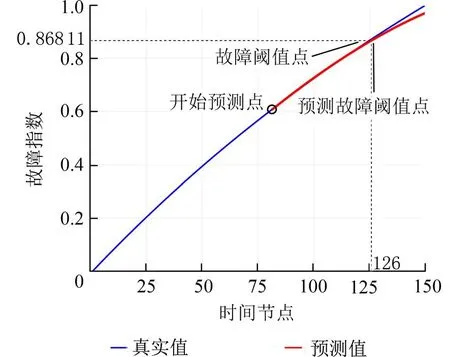
图7 C2-80 的APSO 优化后预测值和真实值Fig.7 Prediction and real value of C2-80 after APSO optimization

图8、9 分别为未优化的SVR 预测模型对电阻R3 和电容C2 的预测结果，其惩罚因子和核函数参数均采用网格搜索法进行选择.图中预测值与真实值的偏差明显大于APSO-SVR 预测模型，由此可知APSO-SVR 预测模型具有更高的预测精度.

图8 SVR 对R3-80 的预测值和真实值Fig.8 Prediction and real value of R3-80 by SVR

对APSO-SVR 预测模型与未优化的SVR 预测模型进行故障预测得到的RUL 值进行比较，如表2所示.APSO-SVR 预测模型对电阻R3 和电容C2进行故障预测得到的RUL 值都更接近于真实值，其绝对误差值分别为0 和1.未优化的SVR 预测模型绝对误差值分别为8 和9，由减少的绝对误差值对比真实RUL 值能知优化后的模型预测精度有较大提升.结果表明，APSO-SVR 预测模型能够更为准确地预测模拟电路的剩余使用寿命.

图9 SVR 对C2-80 的预测值和真实值Fig.9 Predicted and true values of C2-80 by SVR

表2 模拟电路RUL 预测实验结果Tab.2 Results of analog circuit RUL prediction experimental

4 结论

本文提取模拟电路的输出响应的统计特征和小波包能量特征，并将两个特征融合作为故障预测的特征向量，然后采用欧式距离构建故障指示器来表征模拟电路元件的退化过程.最后利用APSO 算法代替传统网格搜索法对SVR 进行参数寻优，建立APSO-SVR 预测模型并进行模拟电路故障预测，估计元件的剩余使用寿命.经实验结果表明，优化后的算法能更加准确地预测出模拟电路发生故障的时间及其剩余寿命时间，为模拟电路故障预测提供了新的方法.