一类时变系数和吸收项的多孔介质抛物系统解的爆破*

欧阳柏平, 肖胜中

(1.广州华商学院 数据科学学院，广东 广州 511300;2.广东农工商职业技术学院，广东 广州 510507)

最近几十年来，有关抛物方程和抛物系统解的爆破问题受到学者们广泛关注。 爆破问题的研究主要涉及解的全局存在、爆破时间的上界和下界、爆破率等，依赖于方程和系统的线性或非线性、空间维数、初始数据以及边界条件。文献[1-4]考虑了三维空间上齐次边界条件(Dirichlet条件和Neumann条件)和Robin边界条件下解的全局存在和爆破问题。文献[5-14]研究了高维空间上非线性边界条件下解的全局存在和爆破问题。文献[15-17]考虑了时变或空变系数的局部和非局部抛物方程和抛物系统解的爆破。文献[18-22]研究了其他偏微分方程解的爆破。从某种意义上，非局部的偏微分方程比局部的偏微分方程更有实际应用价值，因而探讨非局部的抛物方程和抛物系统解的爆破有更强的理论价值和实际意义。然而，对于非局部的数学模型的研究目前存在不少困难，因为局部的数学模型的理论和方法不适用于非局部的情况。关于爆破发生时解的爆破时间界的估计,研究上界的方法较多，而下界较少。

文献[4]研究了依赖于时间的抛物系统解的爆破问题：

在齐次Dirichlet边界条件下，作者得到了三维空间上解的全局存在的条件。同时，在某些约束条件下，得到了三维空间上解的爆破时间的上界和下界估计。

文献[6]研究了非线性边界条件下多孔介质抛物系统解的爆破问题：

在非线性边界条件下，作者得到了Rn(n≥2)上解的爆破条件，以及爆破发生时解的爆破时间的上界和下界估计。

文献[7]研究了如下抛物系统爆破问题：

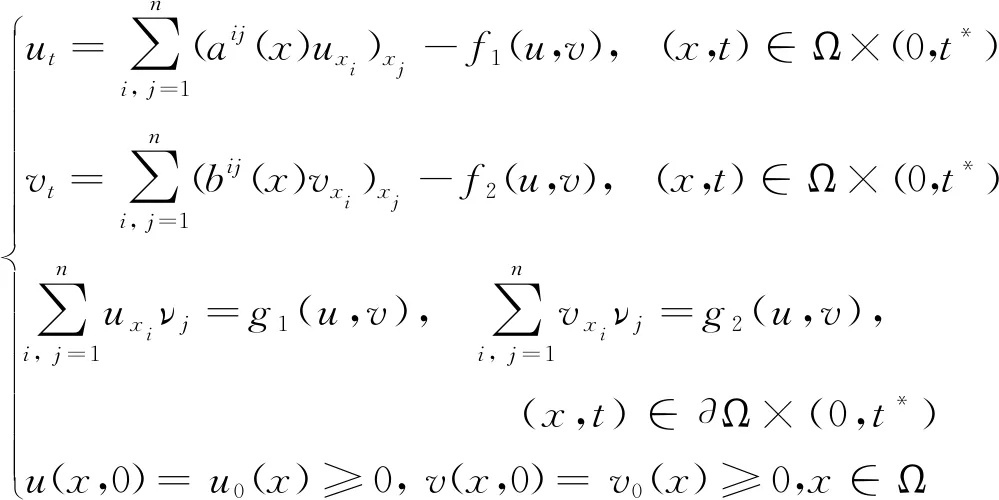
在对初始数据一定的约束条件下,作者得到了高维空间上解的爆破条件以及爆破发生时解的爆破时间的上界和下界估计。

受以上文献的启发，本文研究非线性边界条件下具有时变系数和吸收项的多孔介质抛物系统解的全局存在性和爆破问题：

(1)

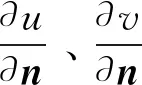
本文主要研究问题(1)解的全局存在性条件和爆破发生时解的爆破时间的下界估计。其难点是如何处理高维空间、非局部项、吸收项，以及非线性边界条件对解的爆破影响。目前,尚未发现有文献研究关于问题(1)的解的全局存在性和爆破问题。

1 全局存在性

本文推导需要用到下面两个引理。

引理1[14]设Ω是Rn(n≥3)上的有界凸区域，则对于u∈C1(Ω),n>0, 有如下不等式：

(2)

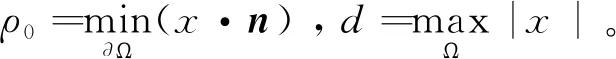
引理2[23]Sobolev不等式

(3)

(4)

其中C=C(n,Ω)，是一个与n和Ω有关的Sobolev嵌入常数。

首先，定义如下辅助函数：

(5)

定理1假设u(x,t),v(x,t)是问题(1)在有界凸区域Ω的经典的非负解,且满足如下条件：

0≤gi(ξ)≤biξsi,ξ>0,bi>0,si、l、m、q、s>1,

(6)

则问题(1)的解所满足的泛函式(5)在任何有限时间都是有界的，即问题(1)的解为全局存在的。

证明运用散度定理，对式(5)求导数，得

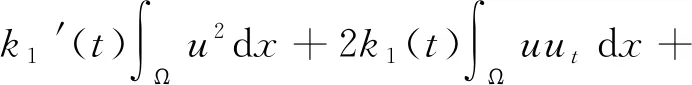
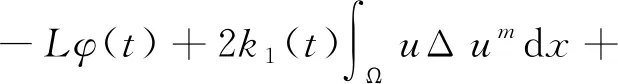
(7)

其中L=min{l1,l2}。

对式(7)右边第二项，由散度定理和式(2)，有

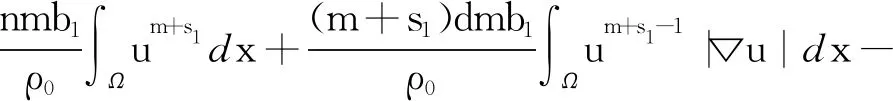
(8)

对于式(8)右边第二项，由Hölder 不等式和Young不等式，得

(9)

式中ε1为正数。

于是，由式(8)和式(9)，得

(10)

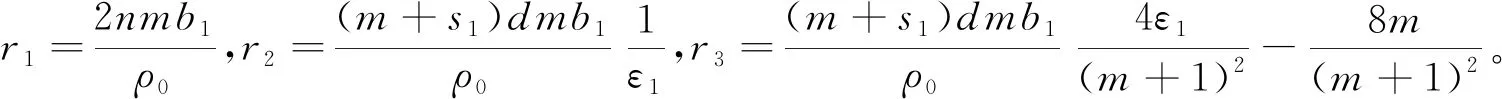
同理，重复式(8)—(10)类似的推导，对于式(7)右边第五项，可得

(11)

对于式(7) 右边第三项，由Hölder 不等式和Young不等式，有

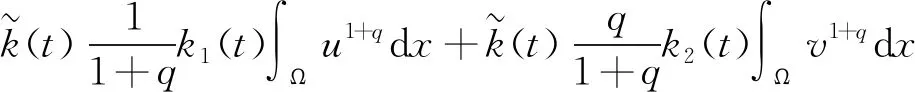
(12)

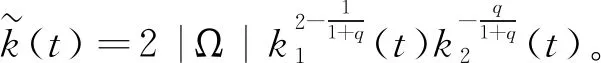
同样地，对于式(7) 右边第六项，由Hölder不等式和Young不等式，有

(13)

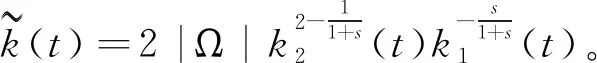
联立式(7)、式(10)—(13)，有

(14)

选取合适的ε1、ε2，使得r3≤0,λ3≤0，于是，式(14)化为

(15)

由Hölder 不等式和Young不等式，得

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

式中ε3,ε4,ε5,ε6,ε7,ε8为正数。

联立式(15)—(23)，有

(24)

其中：

选取合适的ε3,ε4,ε5,ε6,ε7,ε8，使得2-r5>0,2-λ5>0。

由Hölder不等式,可知

由此，可推出

(25)

(26)

联立式(24)—(26)，得

φ′(t)≤(-L+r4+λ4)φ(t)-

(27)

令

由式(27)，可得

φ′(t)≤(-L+r4+λ4)φ(t)-CK1φ(t)1+K2

=φ(t)[-L+r4+λ4-CK1φ(t)K2]

(28)

式中C为正常数。

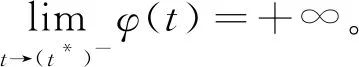
定理1得证。

2 爆破时间的下界

假设下面条件满足

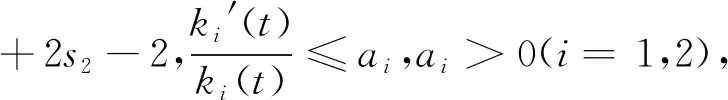
ki(t)>0,t≥0

(29)

构造如下辅助函数：

(30)

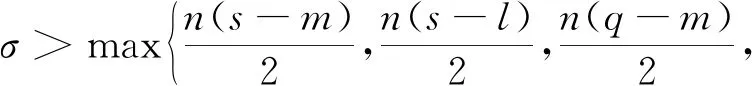
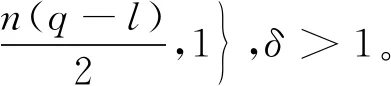
定理2假设u(x,t),v(x,t)是问题(1)、式(29)在有界凸区域Ω的经典的非负解，则式(30)中定义的能量满足微分不等式

φ′(t)≤K6φ(t)+2K7(t)φ(t)ξ1+2K8(t)φ(t)ξ2

由此可得爆破时间t*的下界为

t*≥Θ-1(S)

式中：K6,K7(t),K8(t),ξ1,ξ2,Θ,S均在后面定义；Θ-1为Θ的反函数。

证明对式(30)求导数，并利用条件式(29)，得

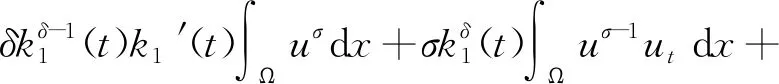
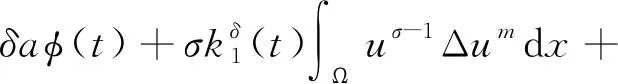
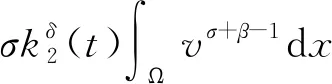
(31)

其中a=max{a1,a2}。

对式(31)右边第二项，应用散度定理和式(2)，有

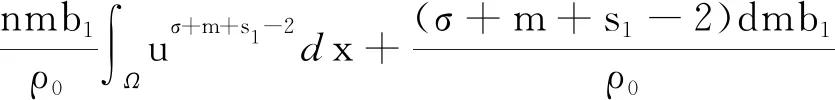
(32)

对式(32) 右边第二项，利用Hölder 不等式和Young不等式，得

(33)

式中ε1为正数。

于是，结合式(32)和式(33)，得到

(34)

其中：

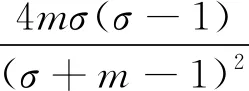
同理，可以推出

(35)

其中：

ε2为正数。

下面处理式(31)右边第三项。利用Hölder不等式和Young不等式，有

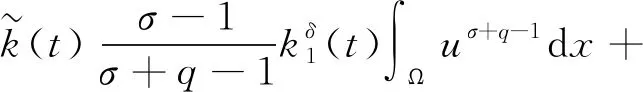
(36)

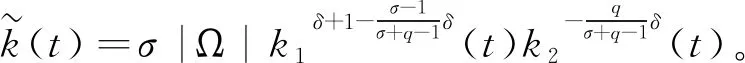
同样地，对式(31)右边第六项，由Hölder不等式和Young不等式，可推出

(37)

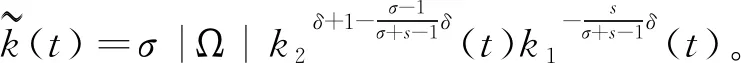
将式(34)—(37)代入式(31)，得到

(38)

再由Hölder不等式和Young不等式，可得

(39)

(40)

(41)

(42)

其中:

ε3,ε4,ε5,ε6为正数。

联立式(38)—(42)，可推出

(43)

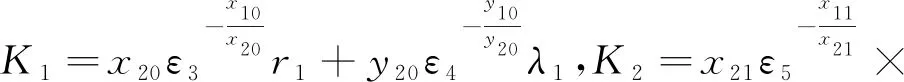
选择恰当的ε3,ε4,ε5,ε6，使得x11ε5(x10ε3r1+r2)-σ≤0,y11ε6(y10ε4λ1+λ2)-σ≤0。

则由式(43)推出

(44)

利用Hölder 不等式和式(3)，有

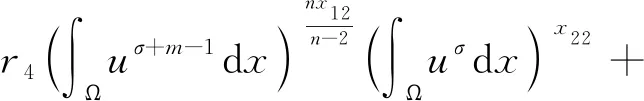
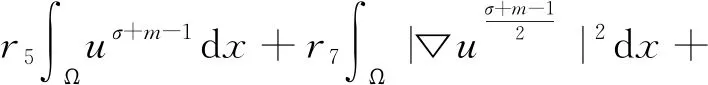
(45)

其中：

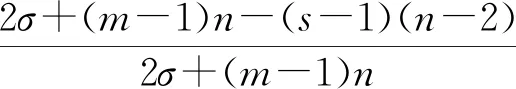
ε7,ε8为正数。

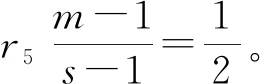
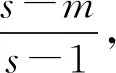
(46)

同样，可得

(47)

其中：

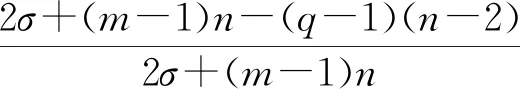
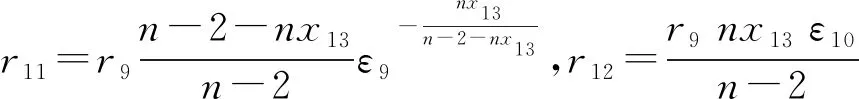
ε10为正数。

类似于式(45)的推导，利用Hölder 不等式和式(4)得

(48)

其中：

ε12为正数。

同理可得

(49)

其中:

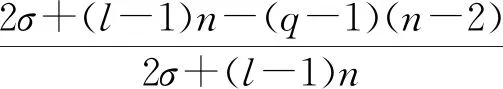
ε14为正数。

将式(46)—(49)代入式(44)，得

φ′(t)≤(δa+K1+K2+K3)φ(t)+

(50)

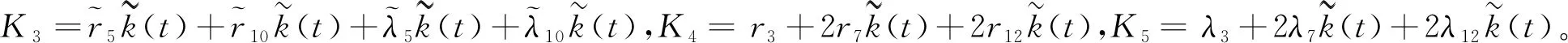
取恰当的ε1,ε2,ε8,ε10,ε12,ε14，使得K4≤0,K5≤0。 则由式(50)可推出

φ′(t)≤K6φ(t)+2K7(t)φ(t)ξ1+2K8(t)φ(t)ξ2

(51)

其中：

K6=δa+K1+K2+K3

设

其中K(t)=1+K7(t)+K8(t)。

对式(51)从0到t*积分，有

(52)

因为ξi>1(i=1,2)，所以式(52)右边积分存在。易知，Θ(t*)是单调递增函数，于是有

t*≥Θ-1(S)

(53)

其中Θ-1是Θ的反函数，从而完成了定理2的证明。