鲁棒迭代学习模型预测控制的实现研究
陈妮
(廊坊热电厂 河北省深州市 065000)
迭代学习控制可以在对之前批次信息的应用下,实现对学习的优化,进而合理调整控制输入轨迹,也就有助于显著提高跟踪性能能,提高跟踪精度。所以这一控制方法在间歇过程控制中的应用较为广泛,然而ILC 为典型开环控制,所以针对系统时域稳定性无法保障,也没有足够的实时干扰处理能力,在应用中需要结合系统反馈控制,以确保系统镇定且对其外部扰动起到抑制作用。针对ILC控制器设计中,通常会忽视被控对象,但是系统收敛性直接受到被控对象数学模型的影响,所以在设计中一定要和被动对象数学模型收敛条件相符。其中就算是在鲁邦反馈控制系统,实现了对ILC 控制器的设计,然而和鲁棒性相关信息并没有得到充分应用。想要对这一问题进行改善,本文在研究中在确保鲁棒性性能加权函数技术上,实现了对单轴ILC 控制器的设计。并通过仿真分析实现对其应用性能的研究。
1 迭代学习控制
本次主要是考虑到CARIMA 离散时间系统模型中所描述的重复过程,具体表示为:
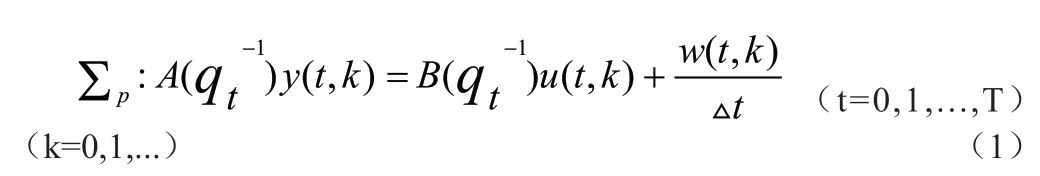
式中:
t——重复中不同个执行周期中的离散时间指标;
k——重复周期指标;
T——各执行周期的固定时间长度;
y(t,k)——重复过程第k 个执行周期的t 时刻输出;
u(t,k)——重复过程第k 个执行周期的t 时刻输入;
w(t,k)——重复过程第k 个执行周期的t 时未知扰动信号;
qt
-1——沿离散时间指标t 的单位平移算子;
∆t——沿离散时间指标t 的单位平移算符,其∆t=1-qt-1;
A(qt-1)——输出信号算子多项式,定义为A(qt-1)=1-a1qt-1+...+ anqt-1;
B(qt-1)——输入信号算子多项式,定义为B(qt-1)=1-b1qt-1+b2qt-1+ ...+bmqt-1。
单纯从形式上来看,以上模型针对重复过程中的输入、输出以及扰动变量全部看成是t 和k 的函数,然而基于表征过程动态算子多项式能够发现,模型仅对沿时间指标的动态特性进行了描述,忽视了沿重复指标k 状态。在各个批次中,如果扰动信号w(t,k)均一致,代表重复过程动态和周期指标没有太大关联性,过程即为完全重复。针对以上公式(1)中所描述的重复过程,迭代学习控制律设计具体为:
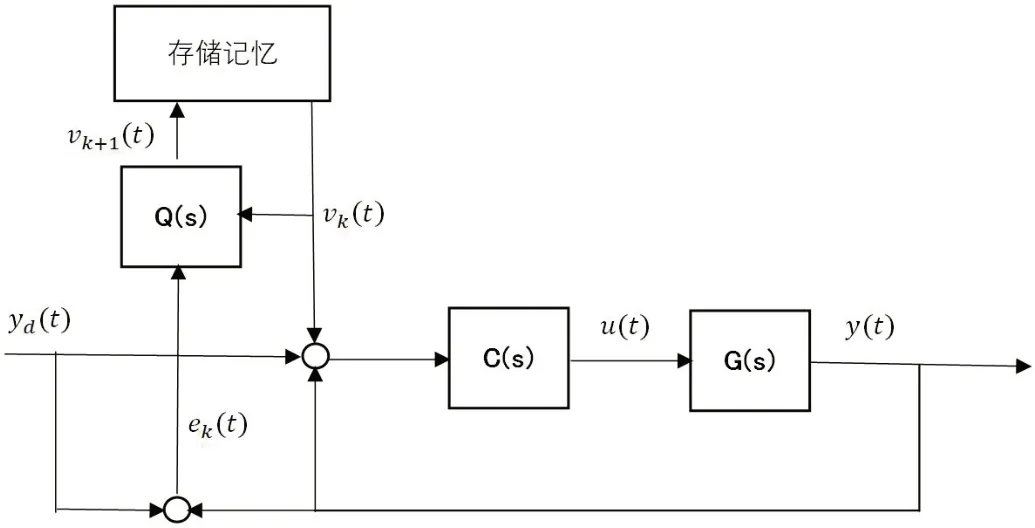
图1:单轴ILC 控制系统

图2:轮廓误差的均方根

式中:
l(t,k)——待设计的迭代更新律;
∆tu(t,0)——初始周期控制增量信号。
以上提出的公式(1)和公式(2)共同组成的控制系统,即为迭代学习控制系统,在设计中重点即为实现确定合理迭代更新律,以能够确保在重复过程中依照期望轨迹跟踪性能,可以在重复过程中逐渐得到改善。
2 鲁棒迭代学习控制器设计
在鲁棒迭代学习模型中,为能够降低各单轴跟踪中存在的误差,本次在鲁棒ILC 控制器设计中,基于性能加权函数实现在各弹轴位置环的设计。在图中yd(t)为期望输出,y(t)和u(t)分别为实际输出和反馈控制输入。另外C(s)代表反馈控制器,对系统稳定性以及鲁棒性提供保障;G(s)代表存在不确定性的被动对象,描述对象主要为:

式中:
Gn(s)——系统标称矩阵;
∆——未知不确定性函数,可以实现对;
Wu(s)——已知不确定性加权函数。
在C(s)设计中,基于鲁棒控制理论中的混合灵敏性问题,相应的引理为:引理1:针对上图1 中的反馈控制系统,G(s)描述详情见公式(3)。由此可得这一系统鲁棒充分必要条件为:

以上公式和以下公式一致:

式中:
S(s)——灵敏度函数,S(s)=1/(1+Gn(s)C(s));
Gn(s)——已知性能加权函数;
T(s)——补灵敏度函数,T(s)=1-S(s)。
单轴ILC 控制系统详情见图1。
在单轴ILC 控制系统中,相应的迭代控制输入vk(s)具体为:

如果v0(s)=0,跟踪误差Ek(s)的计算公式为:

式中:
k——迭代次数;
Q(s)——ILC 控制器下标。
将定理1 中的Q(s)更换为Wp(s),也就能够得到定理2。结合定理2,能够在反馈控制器C(s)设计对性能加权函数Wp(s)应用,进而实现对ILC 控制器Q(s)的控制。在此过程中,不必针对Q(s)单独设计,也可以实现对ILC 系统鲁棒性以及收敛性的保障。但是如果Wp(s)幅值小于等于1 情况下,才能够确保定理2 成立。如果不在这一条件下,剩余误差和学习前误差相比偏大,同时在反馈控制器设计中,为能够降低跟踪误差,Wp(s)幅值一般均会在1 以上。所以针对这一问题,进行了修改,即为定理3。
定理3:针对上图2 中的ILC 系统,迭代学习律见公式(6),如果k →∞情况下,系统的收敛充分必要条件具体为:

通过引理1 和相应的公式能够得出:

由于C(s)可以实现对反馈控制系统鲁棒性的保障,因此以上公式(8)的成立即可以实现对系统充分必要条件成立的保障,具体为:

通过公式(9)能够发现,Q(s)阶次和Wp(s)阶次相比应该偏大,所以Q(s)截止频率和Wp(s)相比应该偏小,以能够实现对曲线下方提供保障。
3 实验仿真分析
基于Matlab 中的鲁棒工具箱实施反馈控制器计算,具体为:
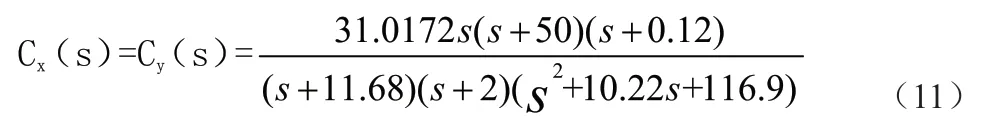

CCC 控制器具体表示为:

期望输出轨迹呈现出四叶草,各单轴的期望输出表示为:

假设在各次迭代中,系统扰动属于是-10~10N 的随机值。初始输出假设为ux0(t)=uy0(t)=0,迭代次数设置为8。对其实施迭代发现,就算是被动对象模型不确定模型受到了随机扰动的影响,然而各个控制器均可以实现对各单轴跟踪误差的降低,且收敛为0。其中轮廓误差均方根详情见图2,从图中能够发现,所完成的CCC 控制器Kc(s)可以显著降低轮廓误差,同时在ILC 作用下也能够确保其基本收敛为0。
本次系统设计的反馈控制器、鲁棒ILC 控制器针对CCC 控制器实施图形轮廓跟踪看出,期望轮廓和实际轮廓在连续实施8 次迭代后,基本实现重合,从这一点可以看出本次设计的控制器可以实现对轮廓的精确跟踪,预测控制效果好。
4 结语
本次研究所得结论:
(1)结合不确定直驱系统鲁棒性条件以及鲁棒收敛条件,实现对单轴ILC 控制器的设计,且完成直驱XY 平台系统模型建构,实现优化设计
(2)这一模型在应用中,和传统ILC 控制器相比,显著提升了跟踪精度及轮廓精度。仿真结果显示这一方法更具有预测控制正确性。

