钻孔承压水头简易测量与承压水Q-S曲线的关系

陈新攀

(紫金矿业集团股份有限公司，福建 厦门市 361006)

矿产资源多深埋于地下，其开发和利用与地下水密切相关。地下水赋存于含水层中。岩层按其渗透性可分为透水层和不透水层。饱含水的透水层是含水层，不透水层称为隔水层[1]。矿床开采涉及的地下水属性通常包括水量、水质、水位（水压）等特征。规范中对地质勘查阶段的水文地质孔要求全部开展分层静止水位观测工作，对单一含水层（组）的钻孔全部需测定终孔稳定水位[2]。

在地质勘查工作中，在井巷施工的钻孔常见地下水涌出孔口的现象，但常由于压力表安装不便或围岩破碎导致地下水从井管周围渗出，导致无法用压力表进行水压测定。本文结合多年的一线工作经验以及水力学基本知识，对采用多组承压水头与流量数据推测稳定承压水头法进行了分析，以期为钻孔涌水的处理提供解决方法。

1 钻孔承压水头简易测量

在地质勘查过程中，特别是井巷内施工的钻孔，常见地下水涌出的现象。钻孔承压水头的测量通常采用压力表测压法，而实际过程中，由于钻探施工对孔口附近的地面破坏较大，关闭水阀，回压地下水时，大量的地下水容易从破碎地面或套管缝隙中涌出，造成测得的水压值偏小，误差较大。

水文地质工作者一般采用接杆测流量和杆长法测得多组流量和杆长值，再通过图解法简单计算稳定水头。由于接杆测流量对水压的影响相对较小，对地面和套管止水的要求相对较低，具有较强的操作性，特殊情况下常替代压力表测量法。具体操作如下。

（1）根据钻孔水文编录求得孔口出水位置与承压含水层顶板距离Z0，测得稳定后的流量Q0；

（2）接一根钻杆，杆长L1，则孔口位置计为Z1=Z0+L1，测得稳定后的流量Q1；

（3）接第二根钻杆，杆长L2，则孔口位置计为Z2=Z0+L1+L2，测得稳定后的流量Q2；

（4）接第三根钻杆，杆长L3，则孔口位置计为Z3=Z0+L1+L2+L3，测得稳定后的流量Q3。

其中，稳定的流量Q为孔口流量与孔口周围渗水量的总和，稳定时间与稳定流抽水试验的要求一致。

机台塔高通常最多只允许续接至3 根钻杆，实际操作中为了拟合计算准确性，通常需接2 根或3根杆。测得多组Z、Q数据，以一次函数关系进行拟合，求得Q为0 时的Z值，此时，Z值表示测压管内流量为0 的位能，即为承压水终孔稳定水头值。

2 承压水Q-S 曲线关系

2.1 裘布依井流理论与承压水Q-S 曲线关系

根据裘布依完整井承压水井流理论，对裘布依完整井承压水公式进行变形整理，可得到承压水公式为：

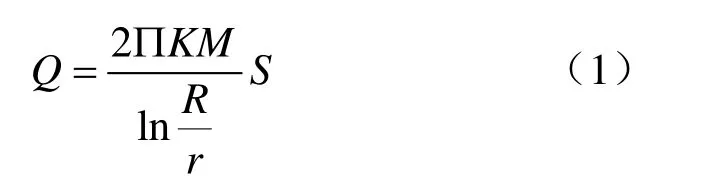
式中，Q为流量，m3/d；K为承压含水层的渗透系数，m/d；M为承压含水层厚度，m；r为抽水井井径，m；S为抽水井水位降深，m；R为承压水或潜水的影响半径（实际计算中以抽水井中心至降深为0 位置的距离为影响半径；但裘布依井流理论的影响半径实质上是含水层的补给半径，在此边界上始终保持常水头[3]，因此理论曲线计算时R值为定值），m。

式（1）中K、M或H、r和R均为固定值，Q、S为未知值，则式（1）中Q与S呈Y=aX的正比例函数关系，a为常数。《专门水文地质学》中对稳定流抽水试验承压水（或厚度很大、降深相对较小的潜水井流）完整井Q−S关系概化为Q=aS的正比例函数关系[4]。

因此，接杆测量位置高程Z和流量Q关系为：

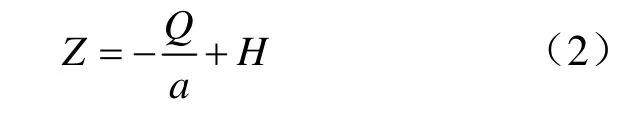
式中，H为总水头。两组及以上的Q、Z值即可求得该二元一次式，即求得终孔稳定水头H值，如图1 所示。

2.2 伯诺里能量方程与承压水Q-S 关系

渗流的基本理论中，根据伯诺里能量方程可得出任一点处液体的总水头为：

式中，Z为位置水头，代表单位重量液体所具有的位能，m；P为渗流压强，m；γ为水的容重；ν为水流的实际速度，m/s；为单位重量液体所具有压能；为测压水头，为动能，m。

假定钻孔揭露完整承压水含水层过程极速，则揭露前后地下水的伯诺里能量方程可概化为如下。

（1）钻孔揭露之前，承压含水层各位置的测压管水头大小相同，承压水近似不流动或动能近似为0。

（2）揭露后，地下水从钻孔四周的承压含水层向孔内流动，并逐渐向上运移至流速为0 的位置水头Z处，承压含水层也逐渐重新达到平衡，各位置测压管水头均相同。

（3）当孔口低于流速为0 的位置水头Z处时，地下水从钻孔内涌出，此时，降深为S，地下水涌出量为Q，整个地下水系统能量方程可重新定义（见图2）：地下水从影响半径R处（断面1）运移至井径r边缘（断面2）处，该过程损失了水头hw1-2值，剩余总水头值H2；地下水由井径r边缘（断面2）进入井内部，继而向上运移至出水口位置（断面3），出水口孔壁压力为0，则由断面1 至断面3 的伯诺里能量方程可表达为：

图2 承压水完整井流伯诺里能量方程示意图

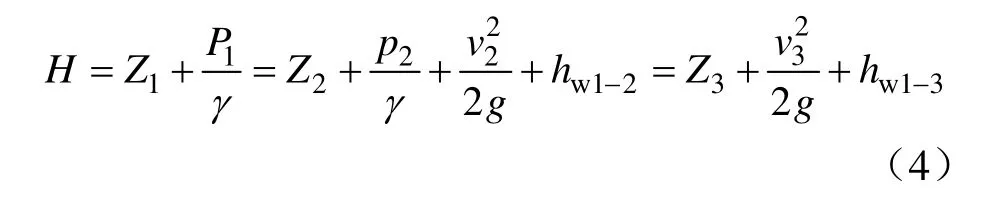
代入Q=Av（A为过水断面面积），得：

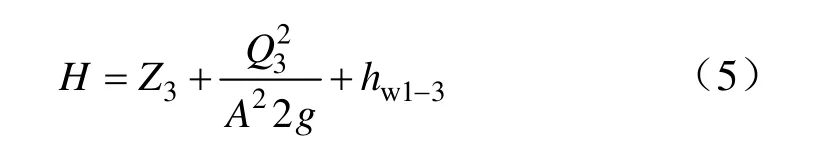
经变换得：

由式（5）可知，位置水头Z与流量Q2成反比，Z与水头损失hw1-3成反比。由于动能转化为位能的转化比极小（v=1 m/d≈0.028 cm/s，流速水头等于3.9×10−7cm）[5]，因此，地下水从断面1 到断面3的能量转换为以水头损失为主。承压水完整井中，当流量Q接近0 时，降深接近0，水头损失亦越少；反之亦然。总体上，位能Z与Q2及能量损失hw成反比，呈现出的二元函数特征，由于能量损失hw和流量、Z的数学关系十分复杂，其函数关系难以定义，在实际运用过程中，需要通过经验公式进行简化。

2.3 抽水试验规程中的Q-S 关系

《水利水电工程钻孔抽水试验规程》中规定，当抽水试验关系曲线Q-S呈曲线时，可采用一个高次方多项式表示，且通常采用4 组Q-S抽水试验数据进行简化计算，如下式：

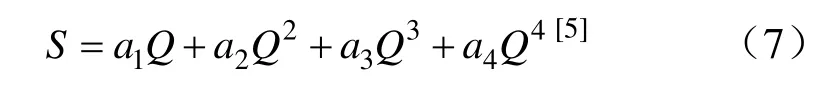
式中，a1、a2、a3和a4均为待定系数，且采用插值均差法求Q—S多项式及其待定参数。代入S=H−Z，得：

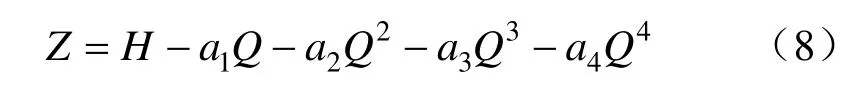
2.4 几种拟合法分析

（1）根据裘布依完整井承压水井流理论，承压水钻孔出水流量Q和位置高程Z关系式可表示为：，Q与Z呈一次函数关系。

（2）根据伯诺里能量方程，位能Z与流量Q的关系式可以表示为：与Q、Z呈较为复杂的关系。

（3）根据《水利水电工程钻孔抽水试验规程》（SL320-2005）相关经验公式显示，Z=-a1Qa2Q2-a3Q3-a4Q4+H。

分析上述3 种函数关系可知，伯诺里能量方程从水力学基本原理角度对钻孔承压水涌水位能与流量关系进行了分析，裘布依完整井承压水井流理论则在稳定流理论的前提下对Q和Z关系进行了探讨，而 《水利水电工程钻孔抽水试验规程》中的公式则是一种具体的Z−Q关系曲线的经验公式。

同时，规程的经验公式中，当除去a2、a3和a4时，可简化为Z=H−a1Q，该式与裘布依完整井承压水井流公式一致，可见，后者为前者的简化版。结合图1 可知，Z−Q拟合曲线，可简化为Z与Q的高次方多项式，并且这个多项式以Z−Q的一次函数关系为上限，分布于该一次函数的左下方。因此，Z−Q一次函数拟合计算时所得Z值为其理论的最大值。

2.5 误差分析

（1）实际抽放水过程中，在井管内测得的水位降深还包括另外两个部分，一是水以高速穿过滤水管时的水头损失，二是井管内部水向上运动到水泵进水阀时的水头损失[6]。因此，实际测得的降深值往往小于理论的水头损失，这将导致拟合的Z值偏小。此外，水井结构，成井工艺及水井附近地下水三维流动都会对Q−S曲线产生影响[6]。

（2）Q−Z拟合过程中，Q、Z表征的状态与稳定流抽水试验要求一致，必须达到稳定状态的流量，而实际测量流量时，往往接杆后地下水整个流态未达稳定状态就测量流量，所测得的Q值往往偏大，导致拟合的Z值偏小。

3 结论

在钻孔施工过程中，对于无法直接采用压力表测量承压水头的钻孔，可以采用接钻杆测得多组流量和杆长值，再通过Z−Q一次函数和Z−Q高次方多项式拟合，其中，一次函数拟合结果宜作为最大的控边值，该方法具有一定的可操作性，在一定情况下可以替代压力表测量法拟合计算稳定水头。