螺栓连接预紧力对结构疲劳性能的影响
乔 乔,李晓秀,周江伟,金福艺
(中国人民解放军第4723 工厂,河北 邯郸 057150)
0 引言
实践表明,在正常服役条件下,机械部件或结构的破坏绝大多数是由疲劳引起的,特别是复杂机械的连接结构,在保证结构完整性的同时,恶劣的工作环境也降低连接结构的稳健性,而完整性与稳健性之间的平衡设计一直是阻碍工业发展的重要因素[1]。航空发动机是典型的高温、高压、高负荷的复杂机械动力装置,随着现代航空工程技术的飞速发展,对航空发动机连接结构稳健性提出了更为严格的要求。螺栓连接结构作为一类重要的紧固连接方式,引起结构简单、拆装方便等特点已在发动机结构设计中大量采用。但是由于技术储备的缺乏,在航空发动机结构布局设计[2]中很多时候依然依靠工程经验,缺乏必要的理论依据。
文沛等[3]针对螺栓在不同使用环境(摩擦因数、工作温度和被连接件刚度等)下,不同外界因素对螺栓连接预紧力的影响展开研究,对于结构关键部位的螺栓连接,在修理及装配过程中应注意采用合理的预紧力加载,已获得较优的力学特征。黄积泽[4]分析研究拧紧技术在汽车装配上对装配质量影响的关系,通过对拧紧技术的常用方法及拧紧工具的选择,可达到提升装配质量的目的。Croccolo 等[5]提供一种试验方法将螺栓连接中的摩擦系数与预紧力准确地关联起来,通过对夹具的拉伸状态试验和数值评估,从而揭示结构疲劳在拧紧过程中的发生过程。周红磊[6]应用有限元及试验的方法,针对航空发动机涡轮部件螺纹连接副强度、高温蠕变损伤及寿命等进行详细研究,探索预紧螺栓连接的蠕变损伤与疲劳寿命的分析方法。洪杰等[7]基于航空发动机动力涡轮转子结构的非连续特征,指出不可恢复滑移、疲劳、摩擦等连接界面接触损伤是转子结构力学特征产生分散性的主要原因,提出对转子支承刚度低敏感区择优的动力特性稳健设计方法。
虽然国内外在对于螺栓预紧对机械结构的力学特征有所研究,但是针对螺栓连接预紧力对疲劳寿命的影响,乃至其在航空发动机部件结构疲劳损伤计算上少有涉及。伴随着结构损伤失效分析理论体系的不断发展与完善,航空发动机的结构稳健性设计逐渐演化为单个部件疲劳损伤优化设计,目前还没有形成比较完善的设计理论方法和工程应用技术体系。
鉴于以上研究背景,本研究首先基于有限元法,分析结构的承载能力和抗变形能力,然后提取结构的单元节点应力张量,经过应力组合转换,并通过Goodman、FKM 的2 种传统应力修正方法进行对比计算,最后基于雨流分析法和Miner 累计损伤准则,对在复杂外载荷作用下的某型航空发动机冷端螺栓连接结构进行疲劳寿命预测,分析螺栓连接预紧力对疲劳寿命的影响,为先进航空发动机连接结构的稳健设计提供理论指导。
1 试验方法
1.1 结构及其有限元模型
螺栓连接结构在航空发动机连接结构设计中大量存在,本研究采用的计算模型为某型航空发动机冷端部件螺栓连接结构,左右部分通过24 个螺栓(规格为M36 mm×340 mm)固紧连接,以保证结构的完整性(图1)。需要说明的是,鉴于垫片的作用主要是减少应力集中对结构造成的损伤,对整体部件结构疲劳影响较小,此处已做适当简化处理。
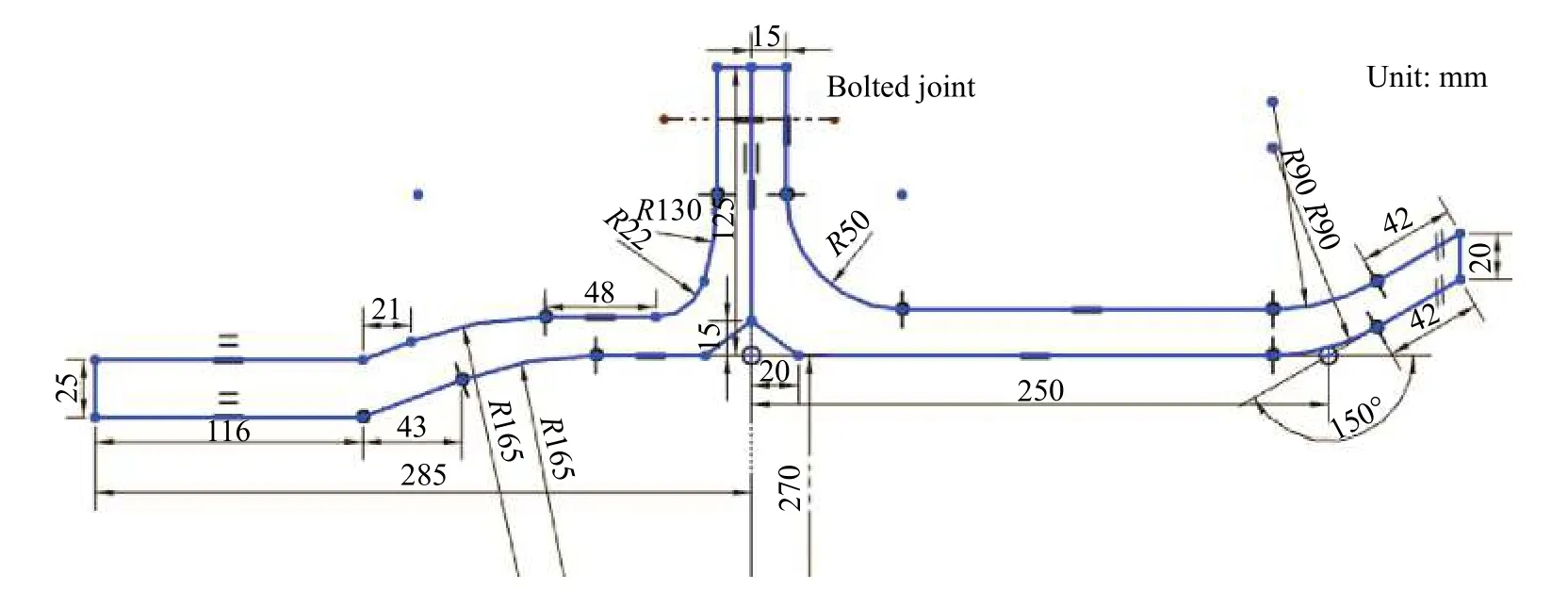
图1 航空发动机冷端局部结构简图Fig.1 Local structure diagram of a certain aeroengine cold end
由于结构为循环周期对称结构,基于商业软件ANSYS Workbench 平台Static Structural-Mechanical 模块建立该结构的1/24 的有限元模型(图2),该有限元模型左、右侧面为循环对称边界面。为了提高计算精度,单元类型均设置为自适应高阶三维高阶实体单元,有关三维实体单元的几何特征及节点配置可参考文献[8],该单元由于其适应性较强且计算精度高,在工程上被广泛采用。其中,螺栓连接处(螺帽和螺杆)采用高阶6 面体单元,且网格已进行加密处理,其余部分为高阶4 面体单元,由此产生16 242 个结点和7921 个单元。在2 部件及与螺栓连接之间的接触部分附加接触单元[9],该接触单元的几何特征,坐标系布置和单元节点的位置如图3 所示。该单元存在2 个节点(i,j),接触面垂直于单元节点连线方向,同时存在初始装配间隙渗透(GAP),图3 中α、β为单元方向角,该单元可以表示任何2 种类型单元的任何2 个节点时间的接触与滑移,有关接触单元的详细力学特征可参考文献[10]。该螺栓连接结构共存在3 处接触,即左右轴段的接触、左轴段与螺栓的接触、右轴段与螺栓的接触,全部定义为摩擦接触,摩擦系数为0.2。

图2 结构有限元模型(单扇区)Fig.2 Structural finite element model (single sector)
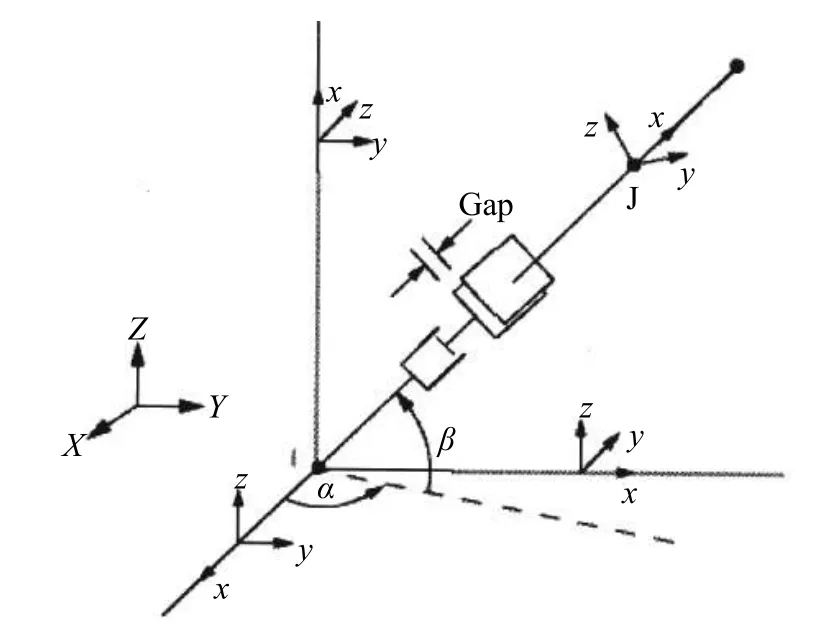
图3 接触单元几何特征Fig.3 Geometrical characteristics of contact elements
螺栓螺母材料为40MnVB,其余材料为Ti-6Al-4V,具体材料参数如表1 所示。

表1 材料力学参数Table 1 Mechanical parameters of materials
1.2 试验流程
为了分析螺栓连接预紧力对结构力学特征的影响,对结构依次施加2、4、6、8 kN 的预紧载荷,并对结构整体施加8500 r/min 的旋转速度载荷,该转速是为了模拟航空发动机转子连接结构在稳态工作时的旋转速度。在分析预紧力对结构疲劳性能影响研究前,分析预紧力对结构静力学特征的影响,即进行结构系统对环境载荷的静响应计算,从结构的静强度和静刚度等方面先确定螺栓连接结构的危险截面位置,这样有助于对静应力对疲劳的影响展开研究。
本研究主要考虑的静力学参数主要有Von-Mises 等效应力和结构整体的最大变形量。Von-Mises 等效应力计算公式为:

式中:σx、σy、σz、τxy、τyz、τzx分别代表单元体在x、y、z方向上所受的正应力和相应方向的剪应力。
一般情况下,每一个计算节点的应力应有9 个应力分量。对结构进行疲劳性能分析时,由于需要将有限元计算结果的应力与材料S-N曲线应力进行等效转换,因此需要找到一个客观评价量。本研究采用危险平面(CriticalPlan)法[11],该方法首先通过雨流计数在多个平面进行扫描计算,确定最大的临界面应力σφ:
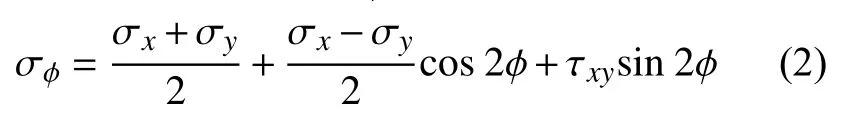
式中:σx、σy、τxy分别为扫描得到危险平面下的正应力x、y相应方向下的正应力、剪应力,φ为危险截面的位置角度。危险面应力组合方法,是疲劳计算中最常用的方法。
虽然应力循环中的主要特征是应力范围影响其材料寿命,但是模型在载荷谱作用下的平均应力也对寿命有着重要的影响,而实际大多情况下受到条件限制,无法得到多条不同平均应力和应力幅的曲线,因此就需要进行修正。鉴于试验数据与真实应力幅-寿命曲线总会存在偏差,故采用2 种应力修正方法,即Goodman、FKM 方法进行对比计算与分析,通过比较2 种方法的计算结果进行择优选取以确保有足够的安全裕度。
由Goodman[12]提出的一种最常用的方法是半应力幅Sr/2 对平均应力Sm所绘制的图形。在图4中,点A表示在交变应力循环下的疲劳强度,而穿过原点O与2 个轴成45°的各条线上的点,则表示脉冲拉应力T和脉冲压应力作用下的疲劳强度。这种图形就是Goodman 试图用平均应力分析表示疲劳强度变动的直接结果的图形。其方程是:

图4 平均应力对疲劳强度影响的Goodman 曲线Fig.4 Goodman curve of the effect of mean stress on fatigue strength
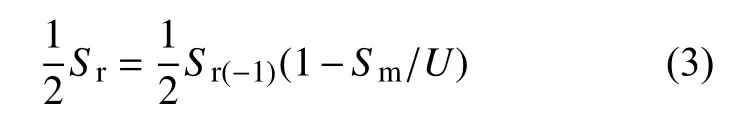
式中:Sr(-1)是在交变载荷(Smin/Smax=-1)下的疲劳强度幅;U是极限抗拉强度,即表1 材料力学参数中的强度极限。
FKM 方法[13]使用的是德国机械工程学会的标准来定义平均应力的敏感度,同时采用名义应力法和局部应力法2 种评估方式来对零部件进行寿命评估,名义应力法适用于低维(一维、二维)结构,而局部应力法适用于多维结构。通过计算出结构的静强度及疲劳强度的安全系数,保证了产品的可靠性和稳健性。该过程的实现已经固定化,可通过ANSYS nCode 疲劳分析与计算模块直接调用,分析流程见图5。由于FKM 规范比较全面的考虑材料或者机械结构破坏的影响因素,已经得到广泛使用。

图5 基于FKM 方法的疲劳强度评估流程Fig.5 Fatigue strength assessment process based on FKM method
在此,Ti-6Al-4V、40MnVB 材料的S-N试验数据如图6 所示。
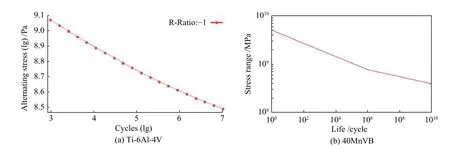
图6 材料Ti-6Al-4V 和40MnVB 的S-N 曲线Fig.6 S-N curve of Ti-6Al-4V and 40MnVB
结构疲劳性能分析出组合应力转换及应力修正方法以外,还应包括结构疲劳寿命与损伤计算。雨流计数法最初是由Matsuiski、Endo 提出,如今在疲劳寿命计算中得到广泛采用。雨流计数法除了计取幅值的变化外,还可同时计取均值的变化,以幅值和均值2 个参数来描述载荷历程,这样比单参数更能反映载荷变化的本质。基于每个节点的载荷参数统计循环周次,累加计算,雨流法在程序中的实现可参考文献[14]。
基于Miner 损伤累计准则[15],一个应力幅为Δs的应力循环所引起的疲劳损伤为1/Ni,ni个应力幅为 Δs的循环周所引起的损伤为ni/Ni,总损伤记为∑ni/Ni。
综上,试验流程应包括结构的静力学分析、组合应力转换及应力修正计算、疲劳寿命与损伤3 部分。
2 试验结果分析
2.1 静力学分析
图7 给出结构Von-Mises 等效应力和最大变形量随螺栓预紧力大小的变化关系。从图中可以看出,随着螺栓预紧力的增加,结构的最大变形量几乎近线性下降,特别在施加预紧力为5 kN 时,结构的最大变形量显著降低。结构的Von-Mises等效应力随着螺栓预紧力的增加先急剧下降,当预紧力达到6 kN 时,Von-Mises 等效应力近乎不变,存在极小值767.91 MPa。可见,较大的预紧力虽然可以优先抑制连接结构的变形量,但是过大的预紧力容易使连接结构发生屈服松脱等现象,严重影响疲劳性能和使用寿命。图8 为螺栓预紧力为6 kN 时的结构受力最大变形和Von-Mises 等效应力的计算结果,结构的最大变形量和等效应力的极值均发生在螺栓连接位置,可见该处是危险位置,螺栓连接的稳健性设计是需要重点考虑。
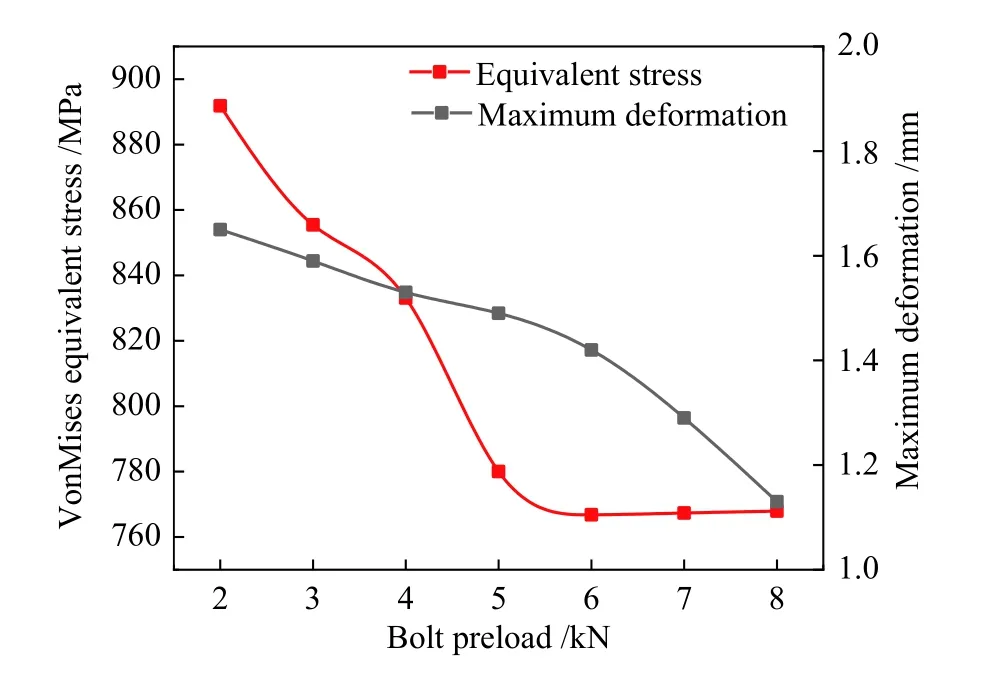
图7 结构等效应力和最大变形量随螺栓预紧力大小的变化关系Fig.7 Relationship between equivalent stress and maximum deformation of structure with bolt preload

图8 6 kN 预紧力作用下结构的最大变形量和等效应力Fig.8 Maximum deformation and equivalent stress of structure under 6 kN preload
2.2 疲劳分析
不同螺栓预紧力下、使用不同方法计算所得结果见表2。螺栓预紧力为8 kN 时,基于FKM 方法得到的疲劳寿命与结构损伤云图如图9 所示,基于FKM 方法得到的损伤云图与此类似。由此可知,损伤最大的位置发生在螺栓连接接触位置。可见,无论是从静力学(等效应力)方面,还是从结构疲劳角度分析,该处都是最危险位置,设计时需要特别注意。
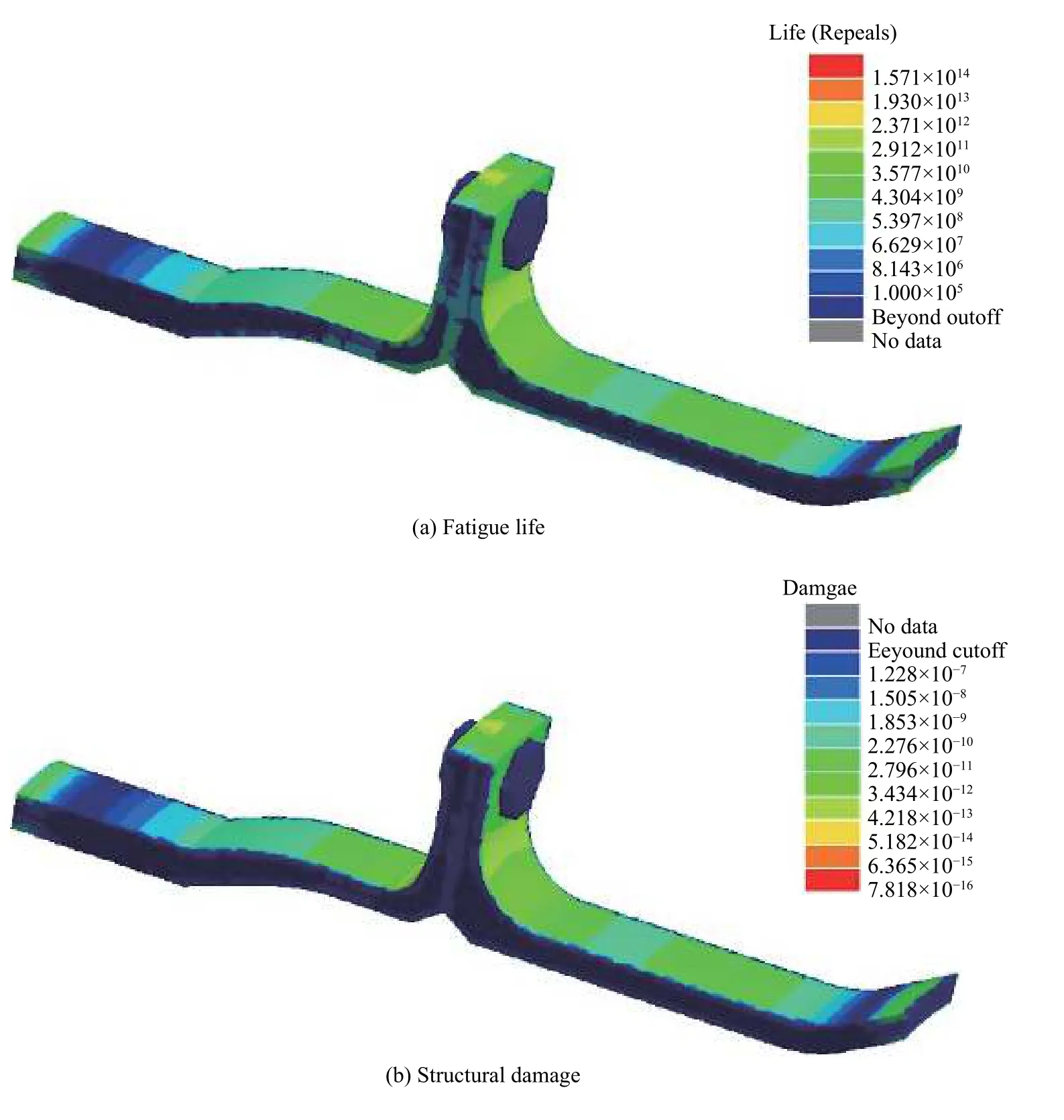
图9 8 kN 预紧力作用下基于FKM 方法的疲劳寿命与结构损伤Fig.9 Fatigue life and structural damage of structure under 8 kN preload by FKM method

表2 基于Goodman、FKM 计算得到的疲劳寿命与损伤Table 2 Fatigue life and damage calculated by Goodman method
图10 为螺栓预紧力随疲劳寿命的变化关系,可以看出,随着结构预紧力的增加,无论是FKM方法还是Goodman 方法,结构疲劳寿命曲线先增加后减小,存在最大的疲劳寿命。算例表明,结构疲劳寿命在螺栓预紧载荷约为5.6 kN 时达到最大,基于Goodman 方法算得的循环周次为8.328×105,基于FKM 方法算得的循环周次为8.262×105,基于FKM 方法得到的疲劳寿命比Goodman 方法得到的疲劳寿命下降0.8%。结构单元最大损伤曲线走势与疲劳寿命相反,即随着螺栓预紧载荷的提高,损伤先降低后增加,在预紧载荷约为5.6 kN时存在虽小损伤点,基于Goodman 方法算得的单元最大损伤为1.206×10-6,基于FKM 方法算得的单元最大损伤为1.211×10-6次,基于FKM 方法得到的结构损伤比Goodman 方法到的结构损伤增加0.4%,安全裕度更高。
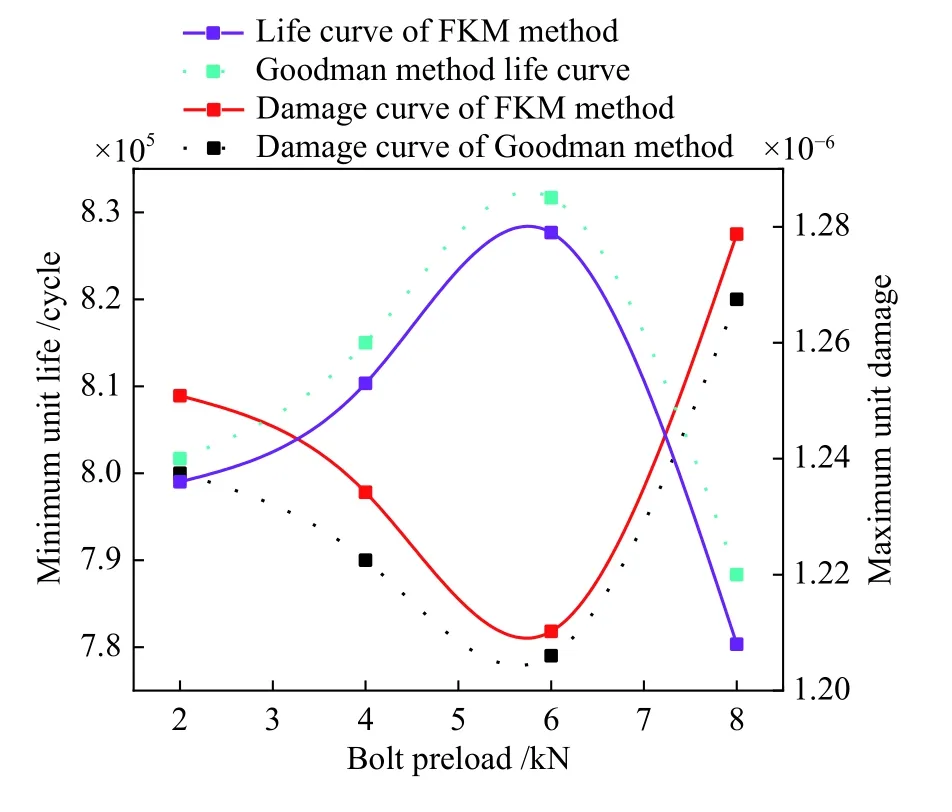
图10 单元最小寿命与最大损伤随螺栓预紧力变化关系Fig.10 Relationship between minimum life and maximum damage of element with bolt preload
3 结论
1)螺栓连接结构预紧力对结构的抗变形能力和结构本身承载能力有着至关重要的影响,过小的预紧力无法保证结构的连续性,过大的预紧力又会影响结构的疲劳寿命,连接结构预紧力的选取对结构力学性能产生直接影响。
2)对于旋转连接结构,随着预紧力的增加,在结构材料屈服强度范围内,其抗变形能力迅速增强,而Von-Mises 等效应力先迅速降低,后趋于不变,存在较低的稳定数值,这也是航空发动机螺栓连接结构预紧力数值需要考虑的初始迭代解。算例结构的Von-Mises 等效应力随着螺栓预紧力的增加,先急剧下降,当螺栓预紧力达到6 kN 时,Von-Mises 等效应力近乎不变,存在极小值767.91 MPa,该值即为预紧力静力学环境下的最优解。
3)随着螺栓连接结构预紧力的增加,结构单元的最大损伤呈现先增加后降低,对应单元最小寿命则先降低后增加。通过螺栓预紧载荷的合理选取,相对于原始设计(螺栓预紧力为8 kN),可将材料的疲劳寿命提高近5.8%,寿命提高4.5×105(循环周次),即预紧载荷存在最优值,可为航空发动机最佳螺栓连接预紧力的确定提供有效手段。
4)FKM 方法与Goodman 方法相比,Goodman方法相对保守,所得疲劳寿命循环周次较大,结构单元最大损伤较小。若采用FKM 方法,其相对最大安全寿命降低0.8%,统计的疲劳寿命循环周次下降6.6×103,对于安全性要求较高的航空发动机连接结构而言,选用FKM 方法有着更高的安全裕度。

